Математика/ 4. Прикладная математика

Фазылова Л.С., Дурмагамбетова А.Г.

Карагандинский государственный университет им. Е.А. Букетова, Казахстан

Численная реализация некоторых одномерных методов решения задач оптимизации

Задачи оптимизации встречаются практически во всех сферах человеческой деятельности, так как любое разумное действие является в определенном смысле и оптимальным.

Оптимизация подразумевает нахождение наилучшего варианта среди всех существующих. В любой практической оптимизационной задаче существует много совпадающих этапов. Наиболее важным этапом является моделирование рассматриваемой физической ситуации с целью получения математической функции, которую необходимо минимизировать, а также определения ограничений, если таковые существуют. Затем следует выбрать подходящую процедуру для осуществления минимизации. Эта процедура должна быть реализована на практике, что во многих реальных случаях вынуждает использовать ЭВМ для выполнения большого объема вычислений.

Универсальных методов, подходящих для поиска экстремума абсолютно любой функции не существует.

Дисциплина «Методы оптимизации» относится к профилирующим дисциплинам при подготовке студентов специальностей «5В011100 – Информатика (в образовании)», «5В060200 – Информаика (естественнонаучная)», «5В070300 – Информационные системые». Важными задачами данного курса является научить студентов создавать математическую модель задач оптимизации и применять алгоритмы методов поиска точек экстремума для решения указанных задач. Студенты должны приобрести навыки численной реализации изученных методов с математических пакетов прикладных программ. Целью данной работы является исследование и применение некоторых методов минимизации функции одной и нескольких переменных для решения задач оптимизации. В данной работе рассматриваются вопросы применения табличного процессора MS Excel при решении задач на условный экстремум.

В задачах оптимизации существует две принципиально различные стратегии выбора точек, в которых производится вычисление функции.

Если все точки задаются заранее, до начала вычислений, - это пассивная стратегия. К данной стратегии относится метод перебора [1].

Если точки выбираются последовательно в процессе поиска с учетом результатов предыдущих вычислений, - это последовательная стратегия. Последовательную стратегию можно реализовать при помощи построения последовательности вложенных друг в друга интервалов, каждый из которых содержит точку минимума. К таким методам относятся метод дихотомии и метод «золотого» сечения [1]. Данные методы можно применять для поиска точек минимума унимодальной функции [1].

Рассмотрим пример реализации метода перебора, метода дихотомии и метода «золотого» сечения для решения одномерной задачи минимизации.

Пример. С точностью 0,01 найти точки минимума и минимальное значение функции и на отрезке .

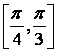Решение. Заданная функция является унимодальной на указанном отрезке. Реализация трех методов решения данной задачи представлена в табличном процессоре MS Excel (рис. 1-3).

С учетом заданной точности в методе перебора требуется 28 вычислений значений функции . Нашли точку минимума и минимальное значение функции (рис. 1).

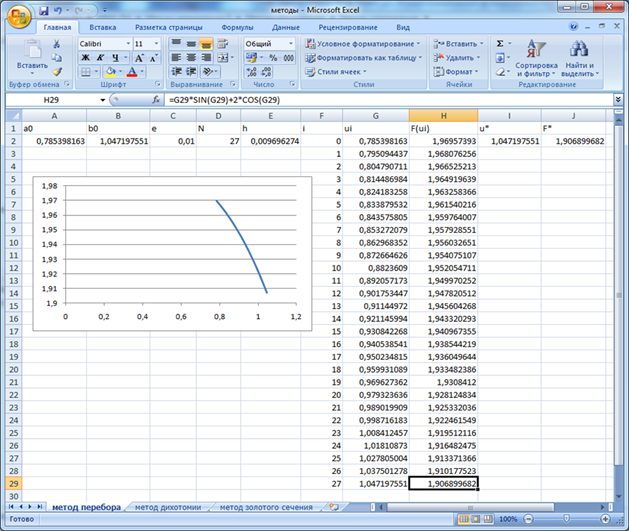
Рис 1. Реализация метода перебора

Более эффективными методами, по сравнению с методом перебора, являются методы последовательной стратегии.

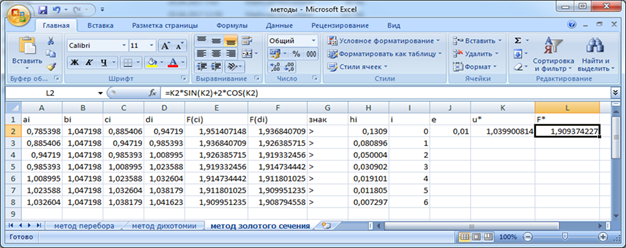
Рис 2. Реализация метода дихотомии

За 6 итераций метода дихотомии найдена точка минимума и минимальное значение функции (рис.2).

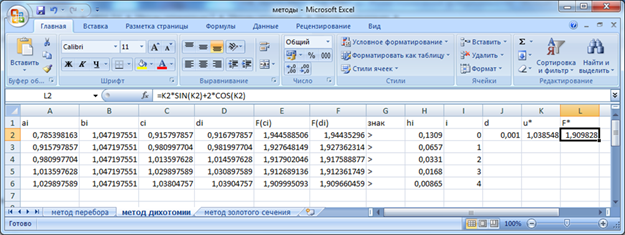
Рис 3. Реализация метода «золотого» сечения

Чтобы решить данную задачу методом «золотого» сечения, потребовалось всего 4 итерации (рис. 3).

Студентам предоставляется возможность сделать сравнительный анализ методов. Метод «золотого» сечения является наиболее эффективным методом.

Преимуществом табличного процессора MS Excel, в контексте изучения студентами данной темы, является закрепление знаний и навыков применения алгоритмов численных методов решения оптимизационных задач [2]. Данный подход позволяет автоматизировать процесс решения задач оптимизации, дает возможность студентам эффективно осваивать материалы курса «Методы оптимизации» и может применяться в учебном процессе.

Литература:

1. Пантелеев А.В. Методы оптимизации в примерах и задачах: Учеб. пособие для студ. ВТУЗов/ Пантелеев А.В.. - М.: Высш.школа, 2008. - 544с.

2. Курицкий Б. Поиск оптимальных решений средствами MS Excel 7.0. - СПб.: BHV - Санкт-Петербург, 2011. – 384 с.