К.ф.-м.н. Докукова Н.A., к.ф.-м.н. Конон П.Н.

Белорусский государственный университет, Минск, Беларусь

Характеристическое уравнение ансамбля n - автономных осцилляторов на подпружиненной платформе с внешним затуханием

Работа посвящена динамическому моделированию, расчету и физическим обобщениям колебаний большого числа метрономов на неподвижной, в начальный момент времени, горизонтальной платформе. Подобные эксперименты широко известны в научной литературе и представлены, в том числе, на видео хостинге YouTube.

Множество метрономов, установленных на свободной поверхности платформы, подпертой упругими пружинами и амортизаторами с общими коэффициентами с и b, на динамической схеме рисунка 1, выводят из состояния покоя, сообщая каждому из тел m_i, начальное отклонение . Маятники метрономов, двигаясь некоторое время с разными амплитудами и фазами, раскачивают платформу и, через непродолжительное время, начинают синхронизироваться по частоте и фазе колебаний. При этом одинаковый для всех метрономов режим движений согласуется с движением горизонтальной платформы.

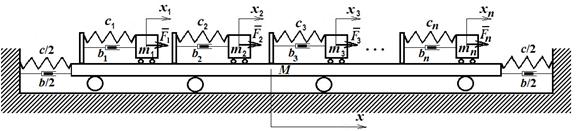
Рисунок 1 - Схема движений n - метрономов на колеблющейся горизонтальной платформе

Для исследования и вывода простых закономерностей влияния параметров механической системы на общий колебательный процесс рассмотрим линейную динамическую схему и уравнения движения в виде

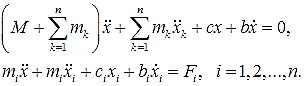(1)

Систему уравнений (1) представим в каноническом виде динамической модели [1 - 3]

где − перемещения масс ; − собственные и парциальные частоты платформы и метрономов; − коэффициенты упругости пружин; r = b/M , r_j = b_j/M, q_j=(1/M+1/m_j) – относительные величины, в которых b и b_j коэффициенты демпфирования соответствующих амортизаторов, обеспечивающих внешнее и внутреннее затухание колебаний; f_j=F_j/M и g_j F_j/m_j – приведенные силы.

Для упрощения расчетов положим, что все собственные и парциальные частоты n метрономов одинаковы , , тогда характеристическое уравнение примет вид:

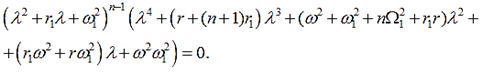, (3)

Условия устойчивости многоэлементной динамической системы и теорема Виета приводят к системе нелинейных алгебраических уравнений для определения частот собственных колебаний

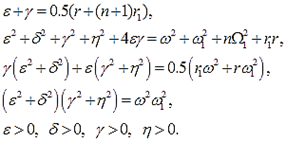
(4)

В общем случае система не разрешима. Задавая числовые значения в правых частях уравнений (4), например, n = 32, c = 1200 н/м, c₁ = 300 н/м, b = 35 нс/м;
b₁ = 8 нс/м; M = 25 кг; m₁ = 0.125 кг при ε = 0.5(r + (n + 1)r₁) - g, получим два набора частот и как точки пересечений поверхностей на рисунках 2.

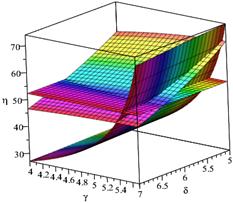
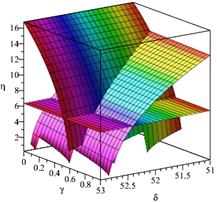
а) e=0.526, d = 6.416, g = 5.454, h = 52.438 б) e= 5.454, d= 52.438, g = 0.526, h = 6.416

Рисунок 2 - Графический поиск частот собственных колебаний

Представлена линеаризованная динамическая модель многоэлементной механической системы с внешним затуханием, выведено характеристическое уравнение общих движений множества автономных осцилляторов на подпружиненной платформе, получены условия устойчивости многоэлементной динамической системы, приводящиеся к системе нелинейных алгебраических уравнений для определения частот собственных колебаний, представлены численные результаты.

Литература:

1. Докукова Н.А., Конон Н.П., Конон П.Н. Влияние внешнего нагрузочного режима на синхронные движения системы автономных осцилляторов// MNPK XI «Perspektywiczne opracowania są nauką i technikami - 2015».Techniczne nauki. Matematyka. Fizyka.− Przemyśl.− 2015. - V. 12. − С. 49-55.

2. Докукова Н.А., Кафтайкина Е.Н., Конон П.Н. Исследование синхроннизации движений нескольких осцилляторов с одинаковыми собственными частотами// МНПК XI «Бъдещето въпроси от света на науката - 2015». Математика. Физика. Съвременни технологии на информации.− «Бял ГРАД-БГ» ООД. − София.− 2015. − Т. 18. С. 13-20.

3. Dokukova N.A., Martynenko M.D., Kaftaikina E.N. // Nonlinear vibrations of hydraulic shock absorbers/ JEPT.- 2008.- V. 81.- N 6,- P. 1197-1200.

4. Dokukova N.A., Kaftaikina E.N., Konon N.P. N sync metronomes on a vibrating horizontal platform// ISPC XIII «Cutting-Edge Science - 2017». Mathematics.- Sheffield, S Yorkshire, England.− 2017.− V. 5.- P. 38-43.