Заец С.Н., д.т.н. Ситников В.С.

Одесский Национальный Политехнический Университет, Украина

Исследование методов повышения точности цифровых корреляционно – экстремальных систем

Вычисление транспортного запаздывания по положению максимума взаимной корреляционной функции является наиболее очевидным и универсальным методом для стационарных эргодических случайных процессов при любом законе распределения. Взаимная корреляционная функция двух случайных процессов, имеет вид:

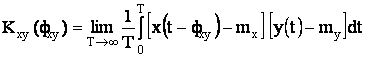
где , - математическое ожидание случайных процессов , ; – временный сдвиг сигнала вносимый коррелометром. При измерении производится оценка при конечном времени выборки T с некоторой методической погрешностью.

Максимум имеется при; при этом равно дисперсии сигнала . Для анализа взаимной корреляционной функции будем использовать нецентрированные сигналы:

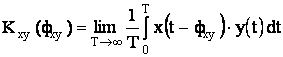
Т.к. при максимуме корреляционной функции , то корреляционная функция примет вид:

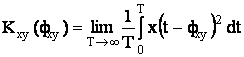
При квантовании сигнала по уровню возникает шум квантования. Амплитуды шума квантования распределены равномерно между значениями и с дисперсией . Квантование проводится по методу округления.

Оценим дисперсию шума квантования поступающую на интегратор.

На интегратор поступает функция . Частота дискретизации равна . Число выборок равно. Пусть дискретизированный во времени сигнал обозначается . А сигнал – обозначается .

На интегратор поступает дисперсия . При округлении результатов умножения добавляется дисперсия округления умножения . Окончательная дисперсия, поступающая на интегратор примет вид:

Сигнал принимает значения . Т.к. , то .

Для оценки дисперсии шума квантования, поступающей на интегратор, обозначим .

Для вычисления взаимной корреляционной функции рассматриваются различные виды интеграторов. Интегрирование проводится по методу прямоугольников, методу трапеций и методу Симпсона.

Выходная дисперсия по методу прямоугольников равна:

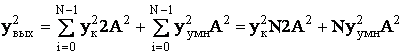
Выходная дисперсия по методу трапеций равна:

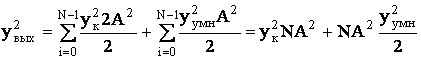
Выходная дисперсия по методу Симпсона равна:

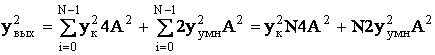
Далее используются следующие обозначения: – разрядность входного сигнала (АЦП); – разрядность умножителя, , , где индексы “ц” и “д” соответствуют разрядностям представления целой и дробной частей соответствующих кодов. В разрядность целой части также входит знаковый разряд. Положительные числа представляются в прямом коде, а отрицательные в дополнительном коде.

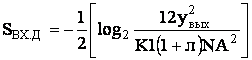
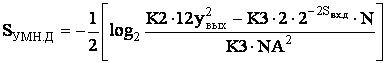
Разрядность сумматоров: .

Дополнительные разряды добавляются к целой части. Количество разрядов гарантирует, что не будет переполнения в сумматоре. Коэффициенты принимают такие значения:

· ; ; – для метода прямоугольников;

· ; ; – для метода трапеций;

· ; ; – для метода Симпсона.

Определим временные затраты на вычисление взаимной корреляционной функции. В качестве вычислительного элемента возьмем микроконтроллеры AVR семейства Mega. Частота тактирования микроконтроллера равна Гц. Время одного цикла равно с.

Общие затраты на вычисление функции по методу прямоугольников равны:

Общие затраты на вычисление функции по методу трапеций равны:

Общие затраты на вычисление функции по методу Симпсона равны:

Покажем полученные результаты графически. Для этого зададимся начальными условиями: время интегрирования ; верхняя частота сигнала ; частота дискретизации ; величина выборки ; абсолютная амплитуда сигнала . Вычислим погрешности интегрирования и временные затраты на вычисления. Пронормируем полученные результаты относительно метода прямоугольника.

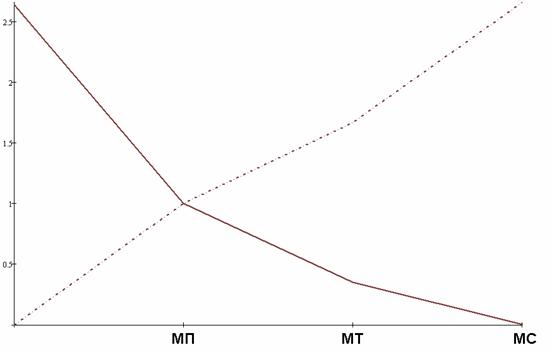
Рис. 1. Погрешность интегрирования и временные затраты на вычисления при различных методах.

МП – метод прямоугольников, МТ – метод трапеций, МС – метода Симпсона.

– погрешность интегрирования, – временные затраты на вычисления.