On large multi-state systems with ageing components reliability and
availability analysis and optimisation
Krzysztof Kolowrocki
Gdynia Maritime University, Poland
Abstract
Basic notions
of the system multi-state reliability analysis are introduced. The multi-state
series system with degrading components is defined and its exact reliability
function is determined. Three methods of multi-state systems reliability
improvement, a warm single reservation of system components, a single warm
reservation of system components and replacing the system components by the
improved components, are proposed and these improved systems reliability
functions are found. The limit reliability function for large multi-state
systems is introduced. An auxiliary theorem on limit reliability function of
large multi-state series systems, which is necessary for their approximate
reliability evaluation, is presented. On the basis of this auxiliary theorem
some corollaries are formulated and proved and then applied to approximate reliability
and availability determination of large multi-state series systems with
improved reliability either by their components hot and cold reservation or by
replacing their components by improved components. Evaluations are given of
multi-state systems reliability functions, their mean lifetimes in the state
subsets and their standard deviations, mean values and variances of lifetimes up to
of exceeding the reliability critical state and availability coefficients. The
results are applied to a large telecommunication network reliability and
availability analysis and optimisation.
1. Introduction
Many technical systems belong to
the class of complex systems as a result of the large number of components they
are built of and their complicated operating processes. Taking into account the
importance of the safety and operating process effectiveness of such systems it
seems reasonable to expand the two-state approach to multi-state approach in
their reliability analysis considered for instance in [1]-[5]. These more
general and practically important complex systems composed of multi-state and
degrading in time components are considered among others in [2] and [5]. An
especially important role they play in the evaluation of large scale technical
systems reliability and safety is defined in [3]. The assumption that the
systems are composed of multi-state components with reliability states
degrading in time without repair gives the possibility for more precise
analysis of their reliability, safety and operational processes effectiveness.
This assumption allows us to distinguish a system reliability critical state to
exceed which is either dangerous for the environment or does not assure the
necessary level of its operational process effectiveness. Then, an important system
reliability characteristic is the time to the moment of exceeding the system
reliability critical state and its distribution. This distribution is strictly
related to the system multi-state reliability function that is a basic
characteristic of the multi-state system. In the case of large systems, the
determination of the exact reliability functions of the systems and the system
risk functions leads us to very complicated formulae that are often useless for
reliability practitioners. One of the important techniques in this situation is
the asymptotic approach [3] to system reliability evaluation. In this approach,
instead of the preliminary complex formula for the system reliability function,
after assuming that the number of system components tends to infinity and
finding the limit reliability of the system, we obtain its simplified form. In
the paper, there are some applications of the presented theoretical results on
large multi-state series systems applying to the evaluation of reliability and
availability characteristics of a large telecommunication network.
2. Multi-state systems with ageing components
In the multi-state reliability analysis to define systems
with degrading (ageing) components we assume that:
Ei, i = 1,2,...,n, are components of a system,
all
components and a system under consideration have the state set {0,1,...,z}, 
the state indexes are
ordered, the state 0 is the worst and the state z is the best,
Ti(u), i = 1,2,...,n,
are independent random variables representing the lifetimes of
components Ei in the state
subset {u,u+1,...,z}, while they
were in the state z at the moment t
= 0,
T(u)
is a random variable representing the lifetime of a system in the state
subset {u,u+1,...,z} while it was in the state z at the moment t = 0,
the system state degrades
with time t without repair,
ei(t) is a component Ei
state at the moment t, 
given that it was in
the state z at the moment t = 0,
s(t)
is a system state at the moment t, given that it was in
the state z at the moment t = 0.
The above assumptions mean that the states of the
system with degrading components may be changed in time only from better to
worse. The way in which the components and the system states change is
illustrated in Figure 1.
transitions
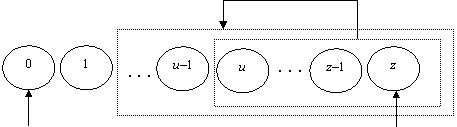
worst
state
best state
Figure 1. Illustration of states changing
in system with ageing components
Definition 1. A vector
Ri(t
) = [Ri(t,0),Ri(t,1),...,Ri(t,z)], i = 1,2,...,n,
where
Ri(t,u)
= P(ei(t) ³ u | ei(0) = z) = P(Ti(u) > t), u = 0,1,...,z,
is the probability that
the component Ei is in the
state subset 
at the moment t, while it was in the
state z at the moment t = 0, is called the multi-state
reliability function of a component Ei.
Definition
= [1,
,...,
],
where
= P(s(t) ³ u | s(0) = z) = P(T(u) > t), u = 0,1,...,z,
is the probability that the system is in the state subset at the moment t, while it was in the
state z at the moment t = 0, is called the multi-state
reliability function of a system.
Definition 
is given by
T(u) = 
, u = 1,2,...,z.
The above definition means
that a multi-state series system is in the state subset if and only if all its
components are in this subset of states.
It is easy to work out
that the reliability function of the multi-state series system is given by
= [1,
,...,
],
where
= 
, 
u = 1,2,...,z.
Definition
Fi(t,u)
= F(t,u), u = 1,2,...,z, i = 1,2,...,n,
i.e. if its components Ei have the same reliability
function
Ri(t,u) = R(t,u)
= 
u = 1,2,...,z, i = 1,2,...,n.
The reliability function of the
homogeneous multi-state series system is given by
= [1,,...,], 
(1)
where
= [R(t,u)]n,
u = 1,2,...,z. (2)
3. Improving reliability of multi-state systems with ageing components
We consider the
homogeneous multi-state series system that is composed of 
components 
with identical
exponential reliability function
R(t
) = [1,R(t,1),...,R(t,z)], (3)
where
for 
(4)
In order to
improve of the reliability of this series system the following exemplary
methods can be used:
a warm single
reservation of system components,
a cold single
reservation of system components,
replacing the system
components by the improved components with the reduced rates of departure
(getting out) 
from the reliability
state subsets 
by a factor 
i.e. components
with reliability functions
R(t) = [1,R(t,1),...,R(t,z)], (5)
where
for (6)
It is supposed here that the reserve
components are identical to the basic ones. The results of these methods of
system reliability improvement are briefly presented below in Corollary 1, giving their multi-state
reliability functions [3].
Corollary 1. If the homogeneous multi-state series system is composed of
components with identical
exponential reliability function given by (3)-(4), then its reliability
function is respectively given by:
Case
= [1,
,...,
], (7)
where
R
for 
(8)
Case
= [1,
,...,
], (9)
where
for (10)
Case 3.
System components with the reduced rates of departures
= [1,
,...,
], (11)
where
for (12)
4. Reliability of large multi-state systems
In the asymptotic approach
to multi-state system reliability analysis we are interested in the limit
distributions of a standardised random variable
u = 1,2,...,z,
where T(u) is the lifetime of
the system in the state subset and
are some suitably chosen
numbers, called normalising constants. And, since
= P(T(u) > an(u)t + bn(u))
= Rn(an(u)t + bn(u),u),
u = 1,2,...,z,
where
Rn(t) = [Rn(t,0),Rn(t,1),...,Rn(t,z)], 
is the multi-state
reliability function of the system composed of n components, then we assume the following definition.
Definition
Â(t) = [1,Â(t,1),...,Â(t,z)],
is called the limit
multi-state reliability function of the system with reliability function Rn(t
) if there exist normalising constants 
such that
Rn(an(u)t + bn(u),u) = Â(t,u)
for t Î CÂ(u), u = 1,2,...,z, (13)
where CÂ(u) is the set of continuity points of Â(t,u).
Knowing the system limit
reliability function allows us, for sufficiently large n, to apply the following approximate formula
Rn(t) @ Â(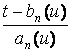
),
i.e.
[1,Rn(t,1),...,Rn(t,z)] @ [1,Â(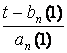
,1),...,Â(
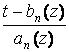,z)], 
(14)
In proving
facts on limit reliability functions of homogeneous multi-state series systems
we can apply either directly Definition 5
or the following lemma [3].
Lemma 1. If
(i) 
= exp[-
], u = 1,2,...,z, is a non-degenerate reliability
function,
(ii) 
= [1,,...,], t Î (-¥,¥), is the reliability function of
a homogeneous multi-state series
system defined by (1)(2),
(iii)
an (u) > 0, bn(u) Î (-¥,¥), u = 1,2,...,z,
then
= [1,
,...,
], t Î (-¥,¥),
is the multi-state limit reliability function of this
system, i.e.
(an(u)t
+ bn(u),u) = 
for t Î 
, u =
1,2,...,z, (15)
if and only if
nF(an(u)t + bn(u),u) = 
for t Î 
, u = 1,2,...,z.
(16)
Direct application of Definition 5
results in the following corollary [3].
Corollary 2. If the homogeneous multi-state series system is composed of components
having exponential reliability functions
R(t,×) = [1,R(t,1),...,R(t,z)], t
Î (-¥,¥),
where
R(t,u) = 1 for t < 0, R(t,u)
= for t ³ 0, u = 1,2,
,z,
and
an(u) =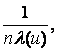 
bn(u) = 0,
u = 1,2,...,z,
then
= [1,
,...,
], t Î (-¥,¥),
where
= 1 for t < 0, = 
for t ³ 0, u = 1,2,...,z,
is its limit reliability
function.
Application of Lemma
1 allows us to prove further two corollaries [3].
Corollary 3. If the homogeneous multi-state series system is composed of components
having reliability functions
R(t,×) = [1,R(t,1),...,R(t,z)], t
Î (-¥,¥),
where
R(t,u) = 1 for t < 0, R(t,u)
= 
for t ³ 0,
u = 1,2,
,z,
and
an(u) =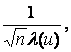 
bn(u) = 0,
u = 1,2,...,z,
then
= [1,,...,], t Î (-¥,¥),
where
= 1 for t < 0, = 
for t ³ 0, u = 1,2,...,z,
is its limit reliability
function.
Corollary 4. If the homogeneous
multi-state series system is composed of components having Erlangs reliability
function of order 2 given by
R(t,×) = [1,R(t,1),...,R(t,z)], t
Î (-¥,¥),
where
R(t,u) = 1 for t < 0, R(t,u)
= [1+
exp[
t] for t ³ 0, 
> 0, u
= 1,2,
,z,
and
an(u) =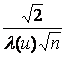 
, bn(u) = 0, u = 1,2,...,z,
then
= [1,,...,], t Î (-¥,¥),
where
= 1 for t < 0, = for t ³ 0, u = 1,2,...,z,
is its limit reliability function.
5. Availability of large multi-state systems
The
following corollary is justified in [6].
Corollary 5. If the components of the homogeneous multi-state renewal
series system with the non-ignored time of renewal with improved reliability
have exponential reliability functions and the system renewal time have a
distribution function with the mean value 
and the variance 
where 
is a system
reliability critical state, then the system availability coefficient at the
moment 
is given by
,
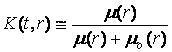while:
Case
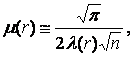
Case
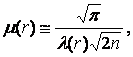
Case 3. System components
with the reduced rates of departures
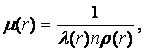
6. Reliability and availability analysis of large telecommunication
network
We consider a part of a
city telecommunication network composed of 
telephone subscribers
cables linked by the head of distributive cables. And, we deal with the
reliability and availability evaluation of the system composed of telephone
subscribers cables only further also called a telecommunication system.
6.1. Reliability of telecommunication network
We assume that the components of the
telecommunication system are five-state (z = 4) and have exponential
reliability functions
t Î (-¥,¥),
where
for 
for 
with
the rates of departure from the reliability state subsets 
given by
, 
Assuming that
the telecommunication system is in the reliability state subset if all its
components are in this reliability state subset, we conclude that the system is
a homogeneous five-state series system and according to (1)-(2), its
reliability function is given by the vector
= [1,
for t ³ 0,
where
=
for t ³ 0, 
=
for t ³ 0,
=
for t ³
0, 
=
for t ³
0.
6.2. Reliability of improved telecommunication network
The
telecommunication system reliability can be improved by a single hot
reservation of its basic components. In this case, using Corollary 3 with normalising constants
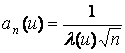
we get the system limit reliability function of the
form
t Î (-¥,¥),
where
for t < 0, = exp[-t2]
for t ³ 0, u = 1,2,...,z.
From the above, considering (14), we get the following
approximate formula
= [1, for t ³ 0,
where
for t ³ 0, 
for t ³ 0,
for t ³
0, 
for t ³
0.
The telecommunication
system reliability can be improved by using double cables composed of one basic
cable and one cable in cold reserve, having identical reliability
functions. In this case, using Corollary 4 with normalising
constants
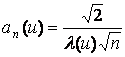
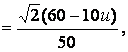
we conclude that the limit reliability function of
this five-state system is
t Î (-¥,¥),
where
for t < 0, = exp[-t2]
for t ³ 0, u = 1,2,...,z.
It means that according to (14), we may use the
following approximate formula
= [1, for t ³ 0,
where
for t ³ 0, 
for t ³ 0,
for t ³
0, 
for t ³
0.
The telecommunication
system reliability can be improved by using improved components having
reliability function
t Î (-¥,¥),
where
for 
for 
u = 1,2,3,4,
with rates of departure from
the reliability state subsets
,
reduced by the coefficient
, 
In this case, using Corollary 2 with normalising constants
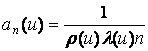
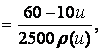
we get the system limit reliability function of the
form
t Î (-¥,¥),
where
for t < 0, = exp[-t]
for t ³ 0, u = 1,2,...,z.
Hence, as from the proof
of Corollary 2 it follows that in
this case formula (14) is exact, we get the following exact formula
= [1, for t ³ 0,
where
for t ³ 0, 
for t ³ 0,
for t ³
0, 
for t ³
0.
All the above results presented in this section allow
us to formulate the following corollary.
Corollary 6. If a critical reliability state
of the telecommunication system is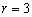 
, then the mean value the standard deviation of the system
lifetime up to exceeding this critical state respectively are:
Case
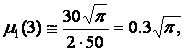
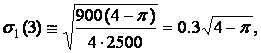
Case
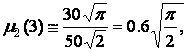
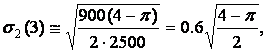
Case 3. System components
with the reduced rates of departures
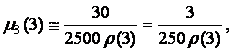
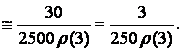
6.3. Availability of improved telecommunication network
Application
of Corollary 5 yields the following
result.
Corollary 7. If the telecommunication system is
renewal, its critical reliability state is 
, its renewal time is not ignored and have a distribution
function with the mean value and the standard deviation respectively given
by
then its availability coefficient is
given by:
Case
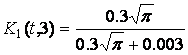
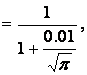
(17)
Case
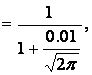
(18)
Case 3. System components
with the reduced rates of departures
,
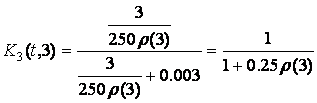(19)
6.4. Effects comparison of telecommunication network
availability improvement
In
order to determine the value of the coefficient 
, by which it is necessary to reduce (multiply by) the rates
of departure of the reliability states subsets of basic components of the
renewal telecommunication system with not ignored time of renovation in order
to receive the system having the same availability coefficient as the
availability coefficient of the system with either hot or cold single reserve
of basic components we can solve either the equation
, 
or respectively the
equation
,
In the first
case, after considering (17) and (19), we get
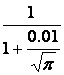
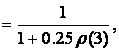
a next
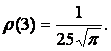
In the second case, after
considering (18) and (19), we get
,
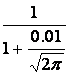
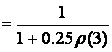and next
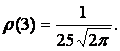
7. Conclusions
In
the paper the asymptotic approach to the reliability and availability
evaluation and improvement of multi-state series systems have been considered.
Theoretical results presented have been illustrated by an example of their
application in reliability and availability evaluation of a large
telecommunication system. These evaluations, despite not being precise may be a
very useful, simple and quick tool in approximate reliability and availability
evaluation and optimisation, especially during the design of large multi-state
systems, and when planning and improving their safety and effectiveness
operation processes. Optimisation of the reliability structures of large
multi-state systems with respect to their operation processes safety and costs
is complicated and often not possible to perform by practitioners because of
the mathematical complexity of the exact methods. The proposed method offers
enough simplified formulae to allow significant simplifying of reliability and
availability optimising calculations.
The results presented in
the paper suggest that it seems reasonable to continue the investigations
focusing on:
- methods of improving
reliability and availability for large multi-state systems with different
structures,
-
methods of reliability and availability optimisation for large multi-state
systems related to costs and safety of the system operation processes.
References
[1] Aven T. (1993). On performance measures for multi-state
monotone systems. Reliability Engineering and System Safety 41, 259266.
[2] Barlow R., Wu A. (1978). Coherent systems with
multi-state components. Mathematics of Operations Research 4, 275281.
[3] Kolowrocki K. (2004). Reliability of Large Systems.
Elsevier.
[4] Lisnianski A., Levitin G. (2003). Multi-state System
Reliability. Assessment, Optimisation and Applications. World Scientific
Publishing Co.
[5] Xue J. (1985). On multi-state system analysis. IEEE
Transactions on Reliability 34, 329337.
[6] Kolowrocki K., Kwiatuszewska-Sarnecka B. (2005).
Asymptotic approach to reliability improvement of mult-state renewal systems,
Chapter