Е.А. Касымов
Казахский национальный
технический университет им.К.И.Сатпаева. г.Алматы.
Республика Казахстан
НОВОЕ ДОКАЗАТЕЛЬСТВО КВАДРАТУРНОЙ ФОРМУЛЫ
.
Известно, что для приближенного вычисления
определенного интеграла
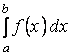 (1)
(1)
используется
интерполяционный многочлен Лагранжа и неизвестные коэф-фициенты определяются с
помощью определенного интеграла, а в этой работе предлагается новый способ
определения неизвестных коэффициентов и оценка остаточного члена квадратурной
формулы Ньютона-Котеса.
Пусть узлы интерполирования расположены
так: ![]() ,
, ![]() и точка
и точка ![]() совпадает с точкой
совпадает с точкой ![]() , тогда предполагаем, что
, тогда предполагаем, что ![]() В этом случае узлы
интерполирования не содержат точек
В этом случае узлы
интерполирования не содержат точек ![]() и
и ![]() , а промежуток интегриро-вания
разбивается этими узлами на
, а промежуток интегриро-вания
разбивается этими узлами на ![]() равных частей. При
этом численного интегрирования, которые получатся в этом случае, будем называть
квадратур-ной формулой Ньютона-Котеса открытого
типа.
равных частей. При
этом численного интегрирования, которые получатся в этом случае, будем называть
квадратур-ной формулой Ньютона-Котеса открытого
типа.
Предположим, что подынтегральная функция ![]() на отрезка
на отрезка ![]() имеет непрерывные
производные девятого порядка включительно.
имеет непрерывные
производные девятого порядка включительно.
Определенный интеграл (1) будем искать в
виде формулы:
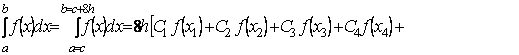
![]() (2)
(2)
где
![]() -узлы интерполирования,
-узлы интерполирования, ![]() извес-тные значения функции
извес-тные значения функции ![]() в узлах
в узлах ![]() -неизвестные коэффициенты, подлежащие определению,
-неизвестные коэффициенты, подлежащие определению, ![]() -остаток квадратурной форму-лы (2), причем узлы и неизвестные
коэффициенты не зависит от выбора под-ынтегральной функции из рассматриваемого
класса функций.
-остаток квадратурной форму-лы (2), причем узлы и неизвестные
коэффициенты не зависит от выбора под-ынтегральной функции из рассматриваемого
класса функций.
Для определения неизвестных коэффициентов ![]() и оценить остаток
и оценить остаток ![]() квадратурной формулы (2), введем новую функцию
квадратурной формулы (2), введем новую функцию ![]() по формуле:
по формуле:
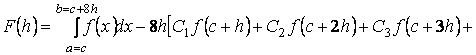
![]() (3)
(3)
Разложим функцию ![]() в ряд Маклорена в
точке
в ряд Маклорена в
точке ![]() :
:
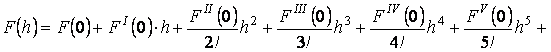
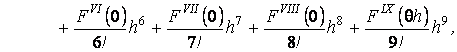 (4)
(4)
где
![]()
Из (3) найдем производные относительно ![]() :
:
![]()
![]()
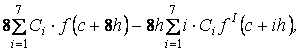
![]()
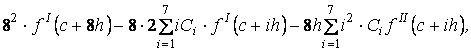
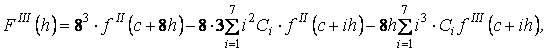
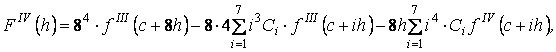
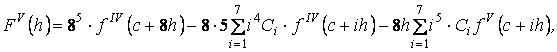
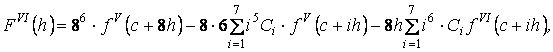
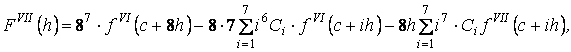
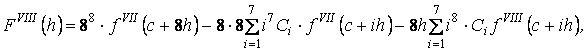 (5)
(5)
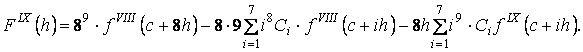
Теперь определим неизвестные коэффициенты ![]() так, чтобы при
так, чтобы при ![]() имели место равенства
имели место равенства ![]() . Тогда из (5) будем иметь сис-тему линейных неоднородных алгебраических
уравнений с определителем Вандермонда относительно неизвестных коэффициентов
. Тогда из (5) будем иметь сис-тему линейных неоднородных алгебраических
уравнений с определителем Вандермонда относительно неизвестных коэффициентов ![]() :
:
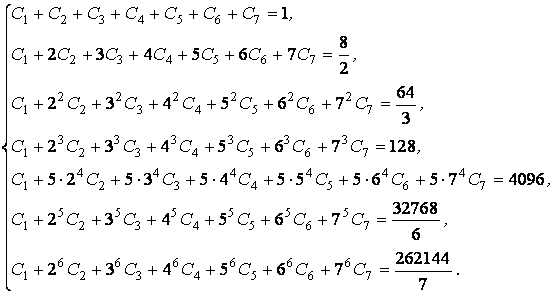
Отсюда
![]() (6)
(6)
т.е.
действительные коэффициенты ![]() квадратурной формулы
(2) равноот-стоящие от концов отрезка
квадратурной формулы
(2) равноот-стоящие от концов отрезка ![]() равны между собой,
причем сумма этих коэф-фициентов равна
единице:
равны между собой,
причем сумма этих коэф-фициентов равна
единице: ![]()
Таким образом, формула (3) с учетом (4), (6) и ![]() имеет вид:
имеет вид:
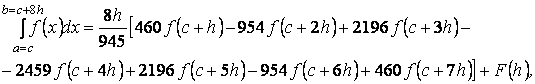 (7) где
(7) где 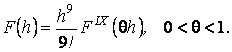
Если сопоставить формулу (2) с формулой (7),
то получим:
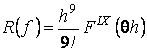 . (8)
. (8)
Рассмотрим
![]() при
при ![]() , а
, а ![]() при
при ![]() . Из (5) при
. Из (5) при ![]() имеем:
имеем:
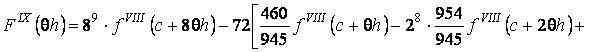
![]()
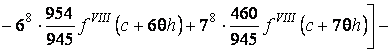
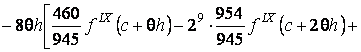 (9)
(9)
![]()
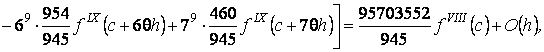
а
при ![]()

Тогда из (8) и (9) имеем:
![]() (10)
(10)
Следовательно, квадратурная формула (7) в
силу (9) и (10) окончательно имеет вид:
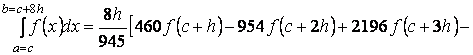
![]() (11)
(11)
а
остаточный член ![]() :
:
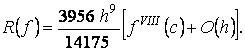 (12)
(12)
Формула (11) с остаточным членом (12)
называется квадратурной формулой Ньютона-Котеса
открытого типа.
Если квадратурную формулу (11) не сразу
применить по всему отрезку ![]() , а разбить его на
, а разбить его на ![]() равных частей длины
равных частей длины ![]() с узлами
с узлами ![]() и к каждой
и к каждой ![]() - частичной части в
отдельности применить формулу (11), то погрешность квадратурной формулы (11)
можно значительно снизить. Для это-го интеграла (1) запишем в виде:
- частичной части в
отдельности применить формулу (11), то погрешность квадратурной формулы (11)
можно значительно снизить. Для это-го интеграла (1) запишем в виде:
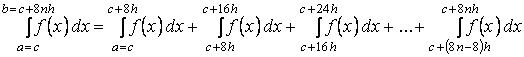 . (13)
. (13)
Теперь применяем к каждому интегралу (13)
формулу (11), тогда получим:
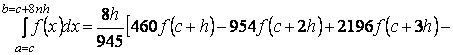
![]()
![]()
![]()
![]()
![]()
![]()
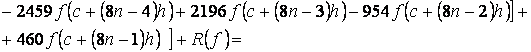
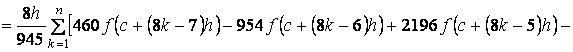
![]()
![]()
![]() (14)
(14)
где 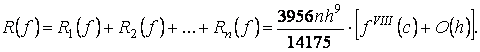 (15)
(15)
Формула (14) с остаточным членом (15)
называется обобщенной квадра-турной
формулой Ньютона-Котеса открытого типа.
Литература
1. Березин И.С., Жидков Н.П. Методы вычислений. Т.1.,-М.; Наука, 1966, -632с.
2. Касымов К.А.,
Касымов Е.А. Квадратурная формула
Ньютона-Котеса //Доклады НАН РК. 2005. №1. С.47-51.