Карачун В.В., Мельник В.Н.
Национальный технический университет Украины «КПИ»
О ВЛИЯНИИ ГАУССОВОЙ КРИВИЗНЫ НА
ПАРЦИАЛЬНЫЕ ЧАСТОТЫ ПОПЛАВКОВОГО ПОДВЕСА
Для
наглядной оценки степени влияния друг на друга колебательных процессов в
подвесе поплавкового гироскопа дифференциальные уравнения подвижной части
удобно записать в виде [1]:
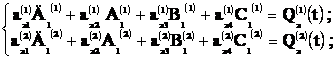
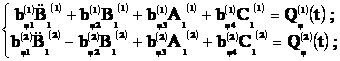(1)
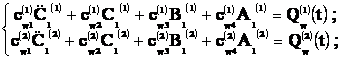
Очевидно, что на упругие перемещения поверхности в каждом
из трех направлений – по протяженности оболочки, вдоль параллели, в радиальном
направлении – влияют двое других.
Представленные три пары уравнений записаны в виде,
позволяющем по первым двум слагаемым определить парциальные (от лат. partialis) частоты. Так,
к примеру, из уравнений (1) получаем:
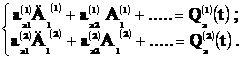
Если принять 
, где 
-
некоторые постоянные, то после двойного дифференцирования получим:
(2)
Отсюда –
Из чего следует, что пары коэффициентов 
,
и 
, 
должны одновременно быть положительными или
отрицательными. В противном случае придется изменять вид функций 
, 
, 
, 
, 
, 
.
Выражения (2) позволяют вычислить парциальные частоты:
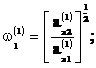
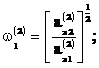
Аналогично, из соотношений определяются парциальные
частоты колебательных процессов в окружном и радиальном направлениях:
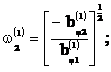
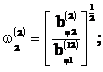
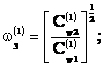
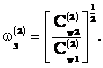
В табл. 1 приведены числовые значения partialis частот для
выпуклой поверхности поплавка гироскопа, то есть при 
, а в табл. 2 – для вогнутой, то есть
при 
.
Таблица 1
Значения partialis частот для выпуклой поверхности поплавка
|
δ \ ω |
|
|
|
|
|
|
|
0 |
1,236 |
1,333 |
0,55 |
0,906 |
0,640 |
0,682 |
|
0,01 |
1,234 |
1,331 |
1,809 |
0,892 |
0,640 |
0,682 |
|
0,02 |
1,232 |
1,330 |
0,556 |
0,878 |
0,639 |
0,776 |
|
0,03 |
1,230 |
1,328 |
0,558 |
0,865 |
0,639 |
0,774 |
|
0,04 |
1,228 |
1,326 |
0,561 |
0,851 |
0,638 |
0,773 |
|
0,05 |
1,226 |
1,324 |
0,564 |
0,838 |
0,638 |
0,771 |
|
0,06 |
1,224 |
1,323 |
0,566 |
0,825 |
0,637 |
0,769 |
|
0,07 |
1,223 |
1,321 |
0,569 |
0,812 |
0,636 |
0,767 |
Продолжение табл. 1
|
0,08 |
1,221 |
1,319 |
0,571 |
0,799 |
0,636 |
0,766 |
|
0,09 |
1,219 |
1,318 |
0,574 |
0,786 |
0,635 |
0,764 |
|
0,10 |
1,217 |
1,316 |
0,576 |
0,773 |
0,634 |
0,762 |
|
0,11 |
1,215 |
1,314 |
0,579 |
0,761 |
0,633 |
0,760 |
|
0,12 |
1,214 |
1,313 |
0,581 |
0,748 |
0,632 |
0,679 |
|
0,13 |
1,214 |
1,311 |
0,583 |
0,736 |
0,631 |
0,678 |
|
0,14 |
1,210 |
1,309 |
0,586 |
0,723 |
0,630 |
0,677 |
|
0,15 |
1,209 |
1,308 |
0,588 |
0,711 |
0,629 |
0,676 |
|
0,16 |
1,207 |
1,306 |
0,590 |
0,699 |
0,627 |
0,675 |
|
0,17 |
1,205 |
1,305 |
0,592 |
0,687 |
0,626 |
0,674 |
|
0,18 |
1,204 |
1,303 |
0,594 |
0,675 |
0,625 |
0,673 |
|
0,19 |
1,202 |
1,301 |
0,597 |
0,663 |
0,624 |
0,672 |
|
0,20 |
1,200 |
1,300 |
0,599 |
0,651 |
0,622 |
0,671 |
|
0,21 |
1,199 |
1,298 |
1,665 |
0,639 |
0,621 |
0,670 |
|
0,22 |
1,197 |
1,297 |
0,603 |
0,627 |
0,620 |
0,669 |
|
0,23 |
1,196 |
1,295 |
0,605 |
0,615 |
0,618 |
0,668 |
|
0,24 |
1,194 |
1,294 |
0,607 |
0,603 |
0,617 |
0,666 |
|
0,25 |
1,192 |
1,292 |
0,609 |
0,591 |
0,616 |
0,665 |
|
0,26 |
1,191 |
1,291 |
0,611 |
0,579 |
0,614 |
0,664 |
|
0,27 |
1,189 |
1,289 |
0,612 |
0,568 |
0,613 |
0,662 |
|
0,28 |
1,188 |
1,288 |
0,614 |
0,556 |
0,611 |
0,661 |
|
0,29 |
1,186 |
1,286 |
0,616 |
0,544 |
0,610 |
0,660 |
|
0,30 |
1,185 |
1,285 |
1,618 |
0,532 |
0,608 |
0,658 |
|
0,40 |
1,170 |
1,270 |
0,636 |
0,411 |
0,592 |
0,643 |
|
0,50 |
1,155 |
1,255 |
0,652 |
0,271 |
0,575 |
0,625 |
Таблица 2
Значения partialis частот
для вогнутой поверхности поплавка
|
-δ \ ω |
|
|
|
|
|
|
|
0 |
1,236 |
1,333 |
0,550 |
0,906 |
0,640 |
0,682 |
|
0,01 |
1,238 |
1,335 |
0,547 |
0,920 |
0,640 |
0,682 |
|
0,02 |
1,240 |
1,337 |
0,544 |
0,934 |
0,640 |
0,681 |
|
0,03 |
1,242 |
1,339 |
0,541 |
0,949 |
0,640 |
0,680 |
|
0,04 |
1,244 |
1,341 |
0,538 |
0,963 |
0,640 |
0,680 |
|
0,05 |
1,246 |
1,343 |
0,535 |
0,978 |
0,640 |
0,679 |
|
0,06 |
1,248 |
1,345 |
0,531 |
0,993 |
0,639 |
0,678 |
|
0,07 |
1,250 |
1,347 |
0,528 |
1.008 |
0,639 |
0,676 |
|
0,08 |
1,252 |
1,349 |
0,525 |
1,023 |
0,638 |
0,675 |
|
0,09 |
1,255 |
1,351 |
0,521 |
1,039 |
0,637 |
0,673 |
|
0,10 |
1,257 |
1,353 |
0,518 |
1,055 |
0,636 |
0,671 |
|
0,11 |
1,259 |
1,355 |
0,514 |
0,934 |
0,635 |
0,669 |
|
0,12 |
1,262 |
1,357 |
0,510 |
1,087 |
0,633 |
0,669 |
|
0,13 |
1,264 |
1,359 |
1,975 |
1,104 |
0,631 |
0,664 |
|
0,14 |
1,267 |
1,361 |
0,502 |
1,121 |
0,629 |
0,661 |
|
0,15 |
1,269 |
1,364 |
0,498 |
1,138 |
0,627 |
0,658 |
|
0,16 |
1,272 |
1,366 |
0,494 |
1,155 |
0,624 |
0,654 |
|
0,17 |
1,274 |
1,368 |
0,490 |
1,173 |
0,621 |
0,650 |
|
0,18 |
1,277 |
1,371 |
0,485 |
1.191 |
0,618 |
0,646 |
|
0,19 |
1,279 |
1,373 |
0,481 |
1,210 |
0,614 |
0,641 |
|
0,20 |
1,282 |
1,376 |
0,476 |
1,228 |
0,610 |
0,634 |
|
0,21 |
1,285 |
1,378 |
0,471 |
1,247 |
0,606 |
0,630 |
|
0,22 |
1,288 |
1,381 |
0,466 |
1,267 |
0,601 |
0,624 |
|
0,23 |
1,291 |
1,383 |
0,461 |
1,287 |
0,595 |
0,617 |
Продолжение табл. 2
|
0,24 |
1,293 |
1,386 |
0,455 |
1,307 |
0,589 |
0,609 |
|
0,25 |
1,300 |
1,389 |
0,450 |
0,753 |
0,582 |
0,601 |
|
0,26 |
1,300 |
1,392 |
0,444 |
1,348 |
0,574 |
0,592 |
|
0,27 |
1,303 |
1,394 |
0,438 |
1,370 |
0,565 |
0,581 |
|
0,28 |
1,306 |
1,397 |
0,432 |
1,392 |
0,556 |
0,573 |
Очевидно,
что имея большую жесткость в направлении протяженности и в окружном направлении
поплавка, partialis частоты 
, 
и 
, 
значительно больше
частот 
( практически на два
порядка). Выпуклость (или вогнутость)
оболочечной части поплавка принципиально не влияет на значения частот 
и 
при 
.
Парциальные частоты в окружном направлении.
Составляющие для выпуклой и
вогнутой боковой поверхности 
принципиально не
отличаются. Составляющая для выпуклого поплавка
имеет тенденцию к систематическому незначительному уменьшению с 0,892 до 0,532
при 
. Если 
, то 
; при 
- 
. Для вогнутого поплавка, парциальная частота постепенно
увеличивается, начиная с 0,906 до 1,437.
Парциальные частоты 
и 
, в радиальном направлении, фактически не изменяются при
изменении величины 
до 
и составляет 
, что на два порядка меньше первых двух. Это в равной степени
относится к выпуклому и вогнутому
исполнению боковой поверхности поплавка.
В
случае цилиндрического поплавка, то есть при
, 
.
Литература:
1. Карачун В.В., Каюк Я.Ф., Мельник В.Н. Волновые задачи
поплавкового гироскопа. –К.: «Корнейчук», 2007. – 228с.