УДК 621.873.2

Бондаренко Л.Н., к.т.н., доц.; Яковлев С.А., соискатель;

Евтух А.О. , курсант 329 гр. (Днепропетровский национальный

университет железнодорожного транспорта им. акад. В. Лазаряна)

Зависимость инерционных сил при пуске

от диаметра колёс крана и тележек

Сила инерции при пуске двигателя механизмов передвижения кранов и тележек определяется из выражения(1)

F_u = (Q + m) V / t_p , (1)

где Q, m – вес груза с грузозахватом и крана или тележек;

V – номинальная скорость;

t_p – время разгона.

Время разгона крана или тележки до номинальной скорости определяется из выражения

t_p = 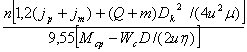, (2)

где n – номинальная частота вращения двигателя;

j_p, j_m – моменты инерции ротора и муфты на валу двигателя;

M_n = 9550N/n – номинальный момент двигателя;

W_c = W_mp + W_y + P_в – статические сопротивления передвижению;

W_mp = (Q + m)(μd + 2k)K_p/D_k – сопротивление от трения в ходовых

частях на прямолинейном участке пути;

μ – коэффициент трения подшипников, приведенный к цапфе колеса диаметром d;

k – коэффициент трения качения колеса по рельсу;

K_p - коэффициент, учитывающий трение реборд.

Отметим, что в справочнике [1] и учебной литературе [2, 3] коэффициент трения качения k для колеса диаметром 400; 500; 560 и 630 мм одинаковый и при плоской головке рельса составляет 0,5 мм. Очевидно, что это не так, поскольку коэффициент трения качения зависит от полуширины пятна контакта, которая не линейно зависит от диаметра колеса [4]. Следовательно, как время пуска (2), так и инерционные силы (1) будут зависеть от диаметра колеса.

Принятие одинаковым коэффициента трения качения для четырёх существенно различных диаметром (максимальная разница 1,6 раза) связано, очевидно с отсутствием аналитической зависимости для его определения.

Было предложено много аналитических зависимостей для определения k, но все они содержат коэффициент, экспериментальное определение которых требует времени и средств больше, чем определение самого коэффициента.

К последним, и на наш взгляд наиболее удачным зависимостям по определению коэффициента трения качения необходимо отнести исследования Д.Табора [5] и Л.Джонсона [6]. Однако, наличие в формуле Табора коэффициента гистерезисных потерь свело „на нет” их практическое применение. Оказалось, что он не совпадает с его величиной, полученной для растяжения и зависящим от большого числа факторов.

Найдём время пуска двигателя крановой тележки без учета ветровых нагрузок, предполагая работу крана в цеху.

Примем для всех указанных выше диаметров колёс, что допускается нормами расчёта, ширину плоского рельса В = 65 мм. Тогда при допускаемых контактных напряжениях σ = 750 МПа (Сталь 65Г по ГОСТ 1050-74 при классификационной группе механизма М5) нагрузка на одно колесо составит Р₄₀₀ = 200; Р₅₀₀ = 250; Р₅₆₀ = 280; Р₆₃₀ = 314 кН, следовательно, вес тележки при условии равномерного распределения давления составит учетверённую величину.

Найдём сопротивление передвижению тележки, воспользовавшись нормативной величиной коєффициента трения качения k = 0,5 мм. При К_р = 2,

d = D_k/6 = 67; 83; 93; 105 мм сопротивления W₄₀₀ = 8,02; W₅₀₀ = 8,98; W₅₆₀ = 9,58; W₆₃₀ = 10,27 кН. Мощность двигателя механизма передвижения при V = 0,6 м/с составит N₄₀₀ = 5,66; N₅₀₀ = 6,34; N₅₆₀ = 6,76; N₆₃₀ = 7,25 кВт.

Теперь воспользуемся более точной величиной коэффициента трения качения. Согласно полученной в [4] зависимости между полушириной пятна контакта b и её коэффициентом трения качения

k = 0,225 be ^-1,2R , (3)

где R – радиус колеса в метрах.

Полуширина пятна контакта при равенстве модулей упругости материалов колёс и рельс, а также равенства коэффициента Пуассона 0,3 [7]

b = 1,526 , (4)

Подставив полученные выше значения Р в формулы (4) и (3), получим значение коэффициентов трения качения k₄₀₀ = 0,515; k₅₀₀ = 0,568; k₅₆₀ = 0,597; k₆₃₀ = 0,613 мм, а мощность двигателей при той же скорости V = 0,6 м/с составит N = 5,75; 6,72; 7,31; 7,88 кВт соответственно.

Сравнительные графики величин, полученных по нормативной методике и предлагаемой для групп классификации М5 показаны на рис. 1а, а на рис. 1б – для группы классификации М1 –М3 (σ = 850 МПа).

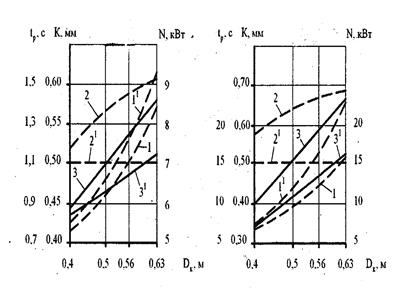
Рис. 1. Зависимость от диаметра колеса: 1.1′ - времени разгона двигателя

тележки соответственно по предлагаемой и нормативной мето-

дикам; 2.2′ - коэффициента трения качения; 3.3′ - расчетной мощ-

-ности двигателя.

Зависимость от диаметров ходовых колёс силы инерции при пуске для группы классификации М5 показана на рис. 2.

Выводы:

- время разгона тележки и инерционные усилия при пуске зависят как от классификационной группы механизма передвижения, так и от диаметров ходовых колёс, для которых нормативная литература рекомендует один и тот же коэффициент трения качения;

- время разгона тележки при группе классификации М5 по предлагаемой методике меньше, чем полученное по нормативной на 1,4% при диаметре колеса D_k = 400 мм и на 7,8% при D_k = 630 мм;

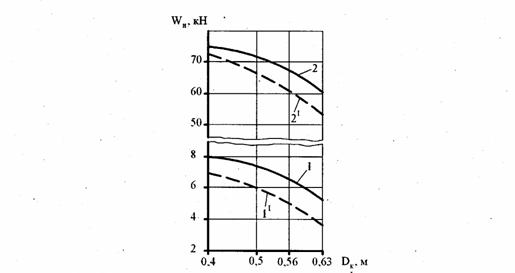
Рис. 2. Зависимость от диаметра ходовых колёс: 1.1′ - инерционных сил

при пуске по предлагаемой и нормативной методикам соответ-

ственно при группе классификации М5; 2.2′ - то же при М1 – М3.

- требуют пересмотра нормативные расчёты времени разгона и инерционных сил при пуске с их увязкой с группой классификации механизмов передвижения.

Литература

1. Справочник по кранам: В 2т.Т 2/Александров М.П., Гохберг М.М., Ко-

вин А.А. и др.- Л.: Машиностроение, 1988.-559 с.

2. Грузоподъёмные машины/Александров М.П., Колобов Л.Н., Лобов Н.А.

и др.-М.: Машиностроение, 1986.-400с.

3. Вайнсон А.А. Подъёмно-транспортные машины. – М.: Машиностроение,

1989.-536 с.

4. Бондаренко Л.М., Довбня М.П., Ловейкин В.С. Деформаційні опори в

машинах.- Дніпропетровськ: Дніпро –VAL, 2002. -200 с.

5. Tabor D. The mechanism of rolling friction: the elastic range. – Proc. Roy.

Soc. Ser. A. Vol. 229. - P.198-211.

6 JonsonK.L. Surfase interfctions between elastically loaded bodies under

tangential forcts. – Proc. Roy. Ser. A. Vol. 203, 1955.-531 p.

7. Справочник по сопротивлению материалов / Писаренко Г.С., Яковлев

А.П., Матвеев В.В. – К.: Наук. думка, 1988. – 736 с.