К.ф.-м.н. Долгарев А.И.

Пензенский государственный университет

решение задачи Ньютона

для движения с тремя степенями свободы

Движение материальной точки с тремя степенями свободы происходит по траектории

= , , (1)

параметр имеет смысл времени. Ускорение движения точки описывается полем

. (2)

Согласно И. Ньютону, поле ускорений движущейся точки определяет закон движения точки – траекторию ее движения. Считается, что линия (1) лежит в евклидовом пространстве , является регулярной класса . Соотношение (2) является уравнением Ньютона, поле задано. В [1] решено уравнение Ньютона для движения с двумя степенями свободы, решение использует методы геометрии Галилея 3-мерного пространства-времени , которая соответствует классической механике Галилея-Ньютона. Ниже решается задача Ньютона для движения с тремя степенями свободы. Применяются идеи 3-мерной геометрии Галилея.

1. Основные понятия теории галилеевых кривых

1.1. Натуральные уравнения кривой.

Пусть действительное линейное пространство аффинного пространства , и векторы из . Галилеевым скалярным произведением векторов и называется

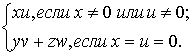= (3)

см. [2, c. 33] Галилеева норма вектора равна

=

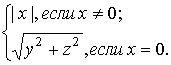
Линейное пространство c галилеевым скалярным произведением векторов (3) называется галилеевым векторным пространством. Компонента вектора называется временной, компоненты называются пространственными, векторы евклидовы. Аффинное пространство с галилевым векторным пространством называется пространством-временем Галилея и обозначается . События , составляющие пространство-время , имеют временную составляющую и пространственные составляющие . Геометрия пространства построена в [2, с. 46 – 101]. Необходимые сведения содержатся и в [1].

Кривая пространства-времени в естественной параметризации описывается векторной функцией

= , . (4)

Считается, что регулярна класса . Кривизна и кручение кривой вычисляются соответственно по формулам

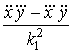, = = . (5)

Решением системы обыкновенных дифференциальных уравнений

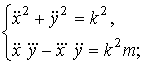(6)

являются функции – пространственные составляющие в (4), функции заданы. Начальные условия

, , (7)

определяют единственную кривую (4), имеющую кривизну и кручение , т.е. , = являются натуральными уравнениями галилеевой кривой.

1.2. Галилеевы кривизны евклидовой кривой

Рассматривается регулярная кривая (1) класса евклидова пространства . Считаем, что . Следствием регулярности кривой (1) является существование функции . Получаем кривую (1) в выделенной параметризации:

, . (8)

Такой же вид имеет галилеева кривая в естественной параметризации, см. (4). В [3] введены галилеева кривизна и галилеево кручение евклидовой кривой (8):

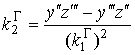, , (9)

см. (5). По этим формулам получаем систему обыкновенных дифференциальных уравнений вида (6):

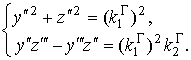(10)

Функции , где , удовлетворяют системе уравнений (10). После двукратного интегрирования указанных функций, находим компоненты задания линии (8). Если =, , то линия плоская, задается векторной функцией , компонента является решением обыкновенного дифференциального уравнения . В этом случае = . Имеем линию постоянной галилеевой кривизны – параболу. При имеется прямая линия. Если =, постоянны, то пространственная линия

=

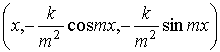
является винтовой (константы интегрирования равны нулю), проекция линии на плоскость есть окружность

=.

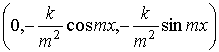Таким образом, всякая евклидова кривая в окрестности обыкновенной точки есть либо отрезок прямой, либо дуга параболы (или окружности), либо дуга винтовой линии. Согласно [4, с. 74 – 75], и парабола и окружность входят в дифференциальную окрестность второго порядка евклидовой линии. Плоская регулярная евклидова кривая в каждой точке обладает соприкасающейся параболой .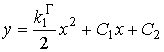

Евклидова кривая однозначно определяется галилеевыми натуральными уравнениями , при этом заданы начальные условия вида (7).

2. Решение уравнения И. Ньютона

для движения с тремя степенями свободы

2.1. Приведение задачи к 2-мерному случаю

Для траектории (8) имеем следующее поле ускорений движения

,

которое соответствует движению с двумя степенями свободы. Величина ускорения движения равна

и совпадает с галилеевой кривизной евклидовой траектории (8): . По второй из формул (9) вычисляется галилеево кручение кривой (8):

= .

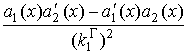Компоненты функции движения (8) отыскиваются как решение системы уравнений (10); единственность функции обеспечивается начальными условиями вида (7). Здесь используются результаты работы [1]. Получена функция движения в выделенной параметризации, нужно еще перейти в этой функции к временному параметру, т.е. должна быть задана функция .

Известно, что ускорение движущейся точки имеет две составляющие – тангенциальную и нормальную: , [5, c. 497], т.е. поле ускорения точки является плоским. С этим фактом согласуется и решение задачи И. Ньютона для движения с тремя степенями свободы, поле ускорений движения по траектории плоское.

В любой параметризации траектория движения точки неизменна, можно изменить ее параметризацию. Предложенная выше схема решения задачи И. Ньютона для движения с тремя степенями свободы позволяет отыскивать траекторию движения точки по полю ускорения.

2.2. Пример отыскания траектории

В [1] рассмотрено движение материальной точки по траектории

,

пример 2 в п. 1.4 и в п. 2.3. Точка движется по конической спирали. Функция обладает обратной . Имеем выделенную параметризацию рассматриваемой линии . По формулам (9) находим:

=, =.

Система (10) такова:

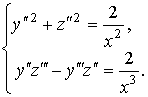
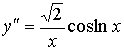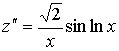Здесь . Положив и , , находим:

Начальные условия: выделяют линию:

= . (11)

Пространственная траектория обладает свойством : , т.е. лежит на круглом конусе и является конической спиралью. Проекция на плоскость конической спирали есть спираль

.

Если время, то точка движется по плоской спирали с мировой линией (11). Если , то траекторией движения является коническая спираль (11), записанная в параметризации

= .

Это другая параметризация линии .

Литература.

1. Долгарев А.И. Натуральные уравнения галилеевой кривой и решение уравнения Ньютона для движения с двумя степенями свободы.// Материали за VII Международна научна практична конференция «Найновите постижения на европейската наука» – 2011. Том 37. Математика. София. «Бял ГРАД-БГ» ООД 2011. – С. 5 – 15.

2. Долгарев А. И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

3. Долгарев А.И., Долгарев И.А. Некоторые приложения галилеевых методов.// Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2009, № 2(9), С. 39 – 59.

4. Фиников, С.П. Курс дифференциальной геометрии. Изд. 2. – М.: КомКнига, 2006. – 344с.

5. Справочник для студентов технических вузов. 2-ое изд, испр. – М.: ООО «Астрель», 2002, 735с.