Педагогические науки/ 5.Современные методы преподавания

Айдос Е.Ж.

Казахский технический университет имени К.И.Сатпаева, г.Алматы

Недифференцируемые функции, представляющие

гладкую кривую

Введение

Основные понятия математического анализа – предел и производная функции в точке, обычно определяются так, что их значениями могут быть только действительные числа. Но иногда, при решении некоторых математических вопросов, мы встречаем применение предела или производной функции с бесконечными «значениями»: (см. напр., ). Вообще, несмотря на невыполнения некоторых арифметических действии над бесконечными числами, их правильное и умелое применение, по нашему, позволит решить более широкий круг теоретических и практических задач математики или могут служить для упрощения сложных математических выкладок. Например, в с помощью производной с бесконечными значениями расширен класс функции, для которых применяются так называемые теоремы о среднем; в теории функции комплексных переменных - сумму конечного числа некоторых интегралов удобно вычислять с помощью одного вычета функции в бесконечной точке (теорема о вычетах) и т.д.

Мы, в этой статье, определяем непрерывность функции в несколько ином виде, чем в обычном, точнее говоря, определяем ее аналогично определению производной в широком смысле, как в и покажем ее роль в решении некоторых вопросов математического анализа. В курсе математического анализа, для изучения вопросов, относящихся к теории гладкой кривой применяются, в основном, непрерывно дифференцируемые функции, представляющие гладкую кривую. Для примера приведем известное определение гладкой кривой.

Определение-1. Кривая заданная параметрическими уравнениями называется гладкой на если - непрерывные функции, имеющие непрерывные производные на отрезке одновременно не равные нулю.

Определение-1 можно применить лишь для кривых, представленных дифференцируемыми на рассматриваемом промежутке функциями, а для кривых, представленных функциями с бесконечными производными, оно непригодно. Но одна и та же кривая может представляться дифференцируемыми, также и недифференцируемыми отображениями. Примерами последней категории гладких кривых могут быть:

дуга окружности кубическая парабола или любая кривая, представленная в виде и т.д.

По определению-1, такие кривые не относятся к гладким, ибо функции, представляющие их, в указанных промежутках не дифференцируемы.

Для установления гладкости этих, вообще для любой кривой можно воспользоваться следующем определеним (см. [2] §6.5, там оно приведено в общем виде).

Определение-2. Кривая называется гладкой на если ее можно задать при помощи уравнении где - непрерывные функции, имеющие непрерывные производные на отрезке одновременно не равные нулю.

Например, если рассмотренную выше дугу окружности параметризовать в виде: то функции удовлетворят условиям определения-2, следовательно по определению-2, дуга окружности – гладкая; а кубическую параболу можно представить в виде где для функции выполняются все условия определения-2, так что кривая также гладкая.

Мы видим, что хотя кривая первоначально задана недифференцируемыми функциями, но если сможем найти ее подходящие параметрические уравнения с составляющими функциями, удовлетворящими условиям определения-2, то она гладкая. Вот этот процесс параметризации кривой с подходящими свойствами функции и является недостатком определения-2. Так как способ параметризации одной и той же кривой, не единственный (например, дуга окружности может быть представлена еще и в виде и т.д.), то такой подход установления гладкости кривой, явно не рациональный.

Ниже мы займемся, в основном, решением отмеченных выше проблем двух определении, укажем характеристику функции по которой можно установить гладкость кривой не переходя к другим параметрическим уравнениям. Такая характеристика позволить также судить о гладкости кривой по гладкости функции .

1. Основные понятия и терминологии

Считаем, что для бесконечностей имеет место соотношения порядка: т.е. бесконечности одного знака равны, а бесконечности разных знаков не равны. Но для бесконечностей без определенных знаков соотношение порядка не распространяется, т.е. выражение или не имеет смысла.

В случае, когда как обычно будем говорить, что «функция в точке имеет предел», а в случае она имеет «конечный предел». Например, функция имеет предел в точке равный а у функции в этой точке предела нет, т.к.

. Аналогично, если имеет место равенство где то «функция в точке имеет производную», а в случае она имеет конечную производную.

Про функцию где будем говорить, что «функция определена в точке в широком смысле». «Функция, определенная в широком смысле в промежутке » в точках этого промежутка может иметь либо конечное значение либо бесконечное: или Например, функция 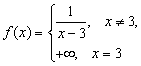определена в интервале в широком смысле, а не определена в точке

Определение (непрерывности в широком смысле). Пусть функция определена в широком смысле в точке и в некоторой ее окрестности. Тогда, если в точке у нее существует предел и выполнено равенство то функция называется непрерывной в широком смысле в этой точке.

Функция 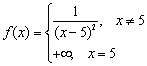непрерывна в точке в широком смысле, ибо

Теперь рассмотрим применение непрерывности функции в широком смысле в решении некоторых вопросов математики.

2. Гладкая кривая и гладкая в широком смысле функция

«Функция, непрерывная в широком смысле в промежутке» - означает, что в точках этого промежутка функция может быть непрерывной или непрерывной в широком смысле.

По нашему, определение гладкой кривой должно формулироваться на языке производной, непрерывной в широком смысле.

Определение–2.1. Кривая заданная параметрическими уравнениями называется гладкой на если - непрерывные функции, имеющие непрерывные в широком смысле производные на отрезке одновременно не равные нулю.

Определение-2.1 применимо для кривых, представленных дифференцируемыми на рассматриваемом промежутке функциями, а также и для кривых, представленных функциями с бесконечными производными.

Аналогическими преимуществами обладает и следующее определение гладкой кривой, заданной явной функцией.

Определение-2.2. Непрерывная кривая называется гладкой, если функция имеет на отрезке непрерывную в широком смысле производную.

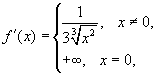Например, по определению-2.2, рассмотренная выше кривая гладкая на любом отрезке, так как производная функции непрерывна в широком смысле в любой точке.

Далее, для функции введем понятие ее угловой функции с помощью равенства

(1)

где непрерывная и монотонная в промежутке функция установливает взаимооднозначное соответствие между расширенным множеством значении производной функций и множеством значении угловой функции так что из существования производной в точке вытекает существование угловой функции в этой точке, и наоборот. Аналогичное утверждение справедливо также для непрерывной в широком смысле производной и непрерывной (в обычном смысле) угловой функции ибо имеет место равенство т.е. Поэтому определение-2.2 будет равносильно следующему определению, сформулированному на языке угловой функции.

Определение-2.3 (на языке угловой функции). Непрерывная кривая называется гладкой, если имеет непрерывную угловую функцию на

Например, рассмотренная выше криваягладкая и по определению-2.3. Действительно, для определена угловая функция, равная 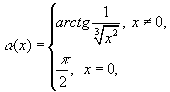и она непрерывна в любой точке. Справедливость последнего утверждения достаточно показать лишь в точке а для остальных точек непрерывность угловой функции следует из известного свойства элементарных функций. Имеем, т.е. функция непрерывна и в точке

Пример-1. Для функции 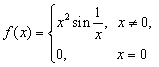определена угловая функция, равная 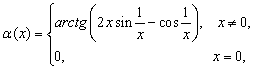но она не является непрерывной в точке (функция в точке не имеет предела), и потому кривая, заданная с помощью функции не гладкая на отрезке, содержащем точку

Так как геометрически, является углом наклона касательной к графику функции в точке с абсциссой x (касательная - направленная прямая), то из существования следует существования касательной в точке с абсциссой x, и обратно. Поэтому используя равенство (1) можно утверждать, что:

если функция имеет в точке производную, то существует касательная к ее графику в точке с угловым коэффициентом и обратно, если существует касательная в точке графика функции f, то функция имеет в точке производную. Другими словами, для функции f между множеством ее производных и множеством касательных к ее графику можно установить взаимооднозначное соответствие.

Аналогичное утверждение для конечной производной – не верно!

Таким образом, для функции f три понятия: «угловая функция», «производная» и «касательная» - равносильны, в смысле их существования, т.е. из существования в точке x одного из них, следует существования двух других.

Пример-2. Для функции на отрезке, содержащем точку не существует угловая функция. Действительно,

Следовательно, у этой функции в точке не существует ни производная, ни касательная.

Пусть для функции f в точке и ее некоторой окрестности определена угловая функция Тогда, касательная в точке графика функции f называется непрерывной в точке если непрерывна угловая функция в этой точке. Касательная графика функции f непрерывна в промежутке если существует непрерывная касательная графика в каждой точке

Определение-2.4 (на языке касательной). Непрерывная кривая называется гладкой, если существует непрерывная на отрезке касательная кривой

Введем понятие гладкой в широком смысле функции.

Определение-2.5. Функция f называется гладкой в широком смысле на отрезке , если она имеет непрерывную в широком смысле производную на этом отрезке.

Определение-2.6. Непрерывная кривая называется гладкой, если функция на отрезке гладкая в широком смысле.

Мы думаем, что понятие непрерывной в широком смысле функции, использованное как инструмент для решения некоторых теоретических проблем математики, может быть также полезным инструментом и в других областях естественных наук по вопросам теоретических и прикладных задач. Поэтому понятия предела, производной, непрерывности функции, определения понятия гладкой кривой и другие вопросы, расмотренные в статье, имели отражения в книге предназначенной для технических вузов.

Литература:

1. Л.Д.Кудрявцев. Курс математического анализа, т.1, «Высшая школа», 1981.

2. С.М.Никольский. Курс математического анализа, т.1, «Наука», 1983.

3. Е.Ж.Айдос. Жоғары математика-2, «Бастау», Алматы 2010.