Несуществование дополнительных первых интегралов в задаче о движении спутника сфероидальной планеты

Физика/1. Теоретическая физика.

К.ф.-м. н. Севрюков П. Ф.

Ставропольский государственные педагогический институт, Россия

Несуществование дополнительных первых интегралов в задаче о движении спутника сфероидальной планеты.

Рассмотрим движение спутника, принимаемого за материальную точку, в поле движения осесимметричной планеты. Если φ и r – планетоцентрическая широта и модуль радиус-вектора, определяющие положение спутника, то в стандартных обозначениях гравитационный потенциал осесимметричной планеты будет иметь вид

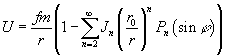, (1)

где f – гравитационная постоянная, т и r₀ – масса и средний экваториальный радиус планеты соответственно, J_n – безразмерные коэффициенты, Р_n – полином Лежандра п-го порядка.

Гравитационный потенциал планеты может быть представлен в виде суммы аппроксимирующего потенциала W и пертурбационной функции R;

U=W+R. (2)

В качестве аппроксимирующего потенциала W выберем потенциал обобщённой задачи двух неподвижных центров [1,2]. Этот потенциал (его ещё называют потенциалом эйлеровой задачи) W включает в себя вторую и третью полностью, а остальные зональные гармоники гравитационного потенциала частично. Члены потенциала (1), не вошедшие в W, составят пертурбационную функцию.

, (3)

где j_n – часть коэффициента J_n, не учтённая аппроксимирующим потенциалом.

Уравнения движения невозмущённой эйлеровой задачи интегрируются в квадратурах [2]. Канонические переменные действие-угол введены в [1] и выражены через эллиптические квадратуры. Дифференциальные уравнения возмущённой эйлеровой задачи принимают наиболее простую форму, если ввести канонические переменные L, G, H, l, g, h, подобные элементам Делоне [1]. Уравнения возмущённого движения в канонических оскулирующих элементах L, G, H, l, g, h будут иметь вид

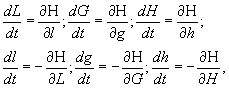(4)

причём

. (5)

Ясно, что в формуле (5) - невозмущённый гамильтониан эйлеровой задачи, R - пертурбационная функция.

Пертурбационная функция может быть записана как кратный ряд Фурье с использованием функций наклона [1] и коэффициентов Ганзена :

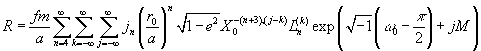, (6)

где a, e, i, ω₀, M – элементы эйлеровой орбиты, являющиеся аналогами большой полуоси, эксцентриситета, наклона, аргумента перицентра и средней аномалии кеплеровской орбиты.

Используя формулы связи элементов эйлеровой орбиты с каноническими оскулирующими элементами L, G, H, l, g, h работы [1], запишем пертурбационную функцию следующим образом:

. (7)

Здесь k и j – любые целые числа.

Выбрав в качестве малого параметра величину μ=r₀c^-¹10^-8, где c – аппликата шаровой точки инерции планеты, представим пертурбационную функцию рядом

, (8)

где каждая функция выражена через переменные L, G, H, l, g и является периодической по угловым переменным , l и g с периодом 2π:

. (9)

Угловая переменная h – циклическая, поэтому уравнения Гамильтона (4) допускают первый интеграл

H=Λ=сonst, (10)

что даёт возможность понизить порядок первоначальной системы уравнений и получить приведённую систему

(11)

с гамильтонианом

(12)

В [3] у Пуанкаре доказана теорема, которая в нашей задаче может быть переформулирована следующим образом.

Пусть движение спутника описывается приведённой системой (11), причём гамильтониан имеет вид (12), тогда если функция H₀ не зависит от угловых переменных l и g, гессиан функции H₀ по переменным L и G не равен тождественно нулю, функции H_i – периодические от , l и g с периодом 2π, то приведённая система не допускает никаких других независимых аналитических первых интегралов, кроме интеграла энергии H=сonst при достаточной малости параметра μ.

Нетрудно проверить, что все условия сформулированной теоремы выполняются. Доказательство основывается на том факте, что если бы в задаче существовал однозначный интеграл, то в разложении пертурбационной функции в кратный ряд Фурье по угловым переменным все коэффициенты должны были бы обращаться в нуль. Изучение разложения R показывает, что это не так. Следовательно, мы должны сделать вывод о том, что приведённая система (11) не может иметь других однозначных аналитических интегралов, не являющихся следствием интеграла энергии. При этом задача о движении спутника сфероидальной планеты не будет иметь дополнительных аналитических первых интегралов, отличных от интеграла энергии и циклического интеграла (10).

Литература.

1. Аксёнов Е.П. Теория движения искусственных спутников Земли. М.: Наука. 1977. 360 с.

2. Дёмин В.Г. Движение искусственного спутника Земли в нецентральном поле тяготения. М.: Наука, 1968. 352 с.

3. Пуанкаре А. Новые методы небесной механики. Т, 1//Пуанкаре А. Избр. Труды Т. 1. М.: Наука, С 8-326.