Технические науки/9. Авиация и космонавтика

м.т.н Романёнок С.Н., Тюпин Р.Л.

Математическая модель низкочастотной вибрации двигателя вертолёта

С учётом свойств объекта исследования и особенностей распространения вибрации в низкочастотном диапазоне, представим ротор газотурбинного двигателя в виде горизонтально расположенного жёсткого ротора, обладающего осевой симметрией и вращающегося с угловой скоростью ω_rt в упругих опорах О₁ и О₂ с коэффициентами жёсткости с₁ и с₂ соответственно. Главный осевой момент инерции обозначим J_x, экваториальные J_y и J_z. Общая масса ротора – m_rt. В опорах учитываются силы вязкого трения с коэффициентами n₁ и n₂. С учётом конструктивных особенностей будем полагать, что перемещения оси вращения вдоль оси ОХ на одной из опор отсутствует.

Для нахождения уравнений вынужденных колебаний воспользуемся уравнением Лагранжа.

(1)

Общая кинетическая энергия системы является суммой кинетической энергии вращения и кинетической энергии перемещения:

(2)

Общая потенциальная энергия работы сил упругости:

(3)

Общая диссипативная энергия работы сил трения:

(4)

Вынуждающие силы статического и динамического дисбаланса описываются следующей системой:

(5)

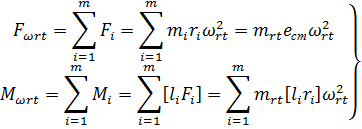
где F_i – вектор центробежной силы действующий на i-й элемент ротора;

m_i – масса i-го элемента ротора;

r_i – расстояние от центра масс элемента до оси вращения ротора;

M_i – вектор момента центробежных сил i-го элемента относительно главной оси инерции ротора, перпендикулярного оси вращения;

e_ст – эксцентриситет ротора;

l – расстояние массы до опор ротора;

ω_rt – круговая частота вращения ротора.

Присвоим значения обобщённым координатам и запишем уравнения вынужденных колебаний:

q₁=x q₂=y q₃=z q₄=φ q₅=ϒ q₆=ψ

Тогда для q₁=x:

a) = =

b) = =

c) = =

Запишем первое уравнение системы в виде:

+= (6)

Для q₂=y:

a) = =

b) = =

c) = =

Запишем второе уравнение системы в виде:

+= (7)

Для q₃=z:

a) = =

b) - = =

c) = =

Запишем третье уравнение системы в виде:

+= (8)

Для q₄=φ:

a) = =

b) - = =

c) = =

Запишем четвёртое уравнение системы в виде:

(9)

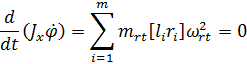
Для q₅=ϒ:

a) = =

b) - = =

c) = =

Запишем пятое уравнение системы в виде:

(10)

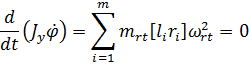
Для q₆=ψ:

a) = =

b) - = =

c) = =

Запишем шестое уравнение системы в виде:

(11)

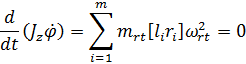
Таким образом, для всей системы в целом:

(12)

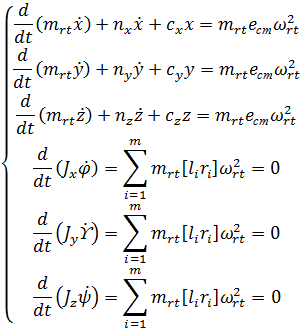
С учётом принятых допущений и особенностей имеющегося оборудования упростим и приведём систему к виду:

(13)

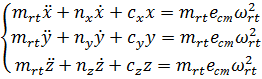
Для сложных систем, которые имеют несколько источников низкочастотной вибрации и конечное число степеней свободы n, подвергающихся воздействию внешних гармонических возбуждающих сил, справедлива общая форма представления в матричной форме [1, 2, 3, 29]:

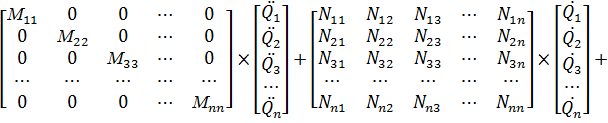
(14)

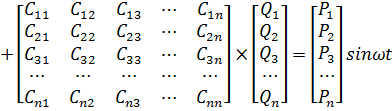
Введём обозначения:

М – диагональная инерциальная матрица:

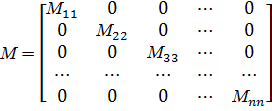
N – матрица коэффициентов демпфирования:

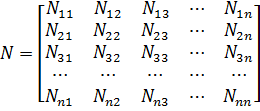
C – матрица коэффициентов жёсткости:

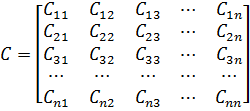
– вектор-столбцы перемещений i-той формы и первой и второй производных соответственно:

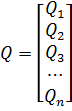
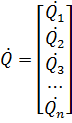
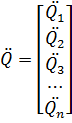
P – вектор-столбец обобщённых возмущений:

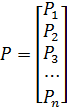
Используя введённые обозначения, приведём выражение (14) к виду:

(15)

С учётом 2.14 и 2.15 запишем:

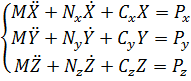(16)

Особенности элементов диагностируемой системы, их взаимодействий описываются элементами матриц М, N, С. Характеристики возбуждающих сил задаются вектором Р.

Матрица N учитывает диссипативные силы действующие в системе. Для данного случая демпфирование принимается линейнозависимым. Коэффициенты демпфирования N_ij зависят как от демпфирования в опорах, так и от демпфирования газовоздушного потока, рассчитываются и уточняются исходя из характера взаимного влияния источников вибрации и с учётом особенностей конструкции.

Элементы матрицы С представляют собой усилия соответствующие перемещению типа i обусловленным равным единице перемещением типа j. Для линейно упругих систем с малыми перемещениями матрица жёсткости является симметричной.

Для реализации динамических моделей пригодны методы численного интегрирования дифференциальных уравнений (метод Эйлера, метод Рунге-Кутта, метод Адамса и др.)

Отклик модели без дефектов на возбуждающее воздействие представлен на рисунке.

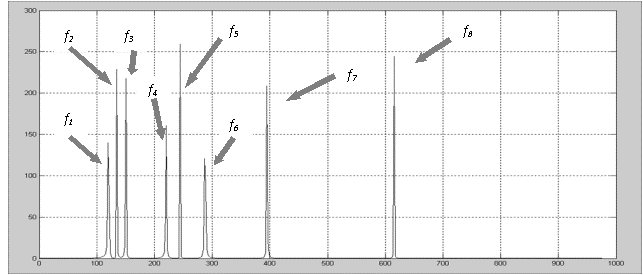
f₁ – привод гибкого валика; f₂ – СТГ-3; f₃ – свободная турбина ТВ3-117; f₄ – вторая ступень редуктора АИ-9В; f₅ – турбокомпрессор ТВ3-117; f₆ – главный привод ТВ3-117; f₇ – первая ступень редуктора АИ-9В; f₈ – ротор АИ-9В.

Литература

1. Ден Гартог Дж. Механические колебания. - М.: Физматгиз 1964г. - 420 стр.

2. Берестнев О.В., Гоман А.М., Ишин Н.Н. Аналитические методы механики в динамике приводов. – Минск.: Наука и техника, 1992. – 238 с.

3. Тимошенко С.П. и др. Колебания в инженерном деле // Перевод с англ. Л.Г. Корнейчука; Под редакцией Э.И. Григолюка. – М.: Машиностроение, 1985. – 472 с.

4. Колесник И.В. Устранение вибрации машин. – М.: Машгиз 1960г. – 650 стр.

5. Генкин М.Д., Соколова А.Г. Виброакустическая диагностика машин и механизмов.- М.: Машиностроение, 1987.-283с.