Современные информационные технологии/1. Компьютерная инженерия

cand. tech. sci. Semakhin A.M.

Kurgan State University, Russia

THE OPTIMUM DECISION OF INTEGER MODEL OF INFORMATION SYSTEM BY THE BRANCH AND BOUND METHOD

The branch and bound method (BB method) is applied to the decision in full or in part integer problems of linear programming. A. Land and A. G. Doig have offered BB-method in to 1960 /1/.

In the beginning of iteration of the BB method it is necessary to have:

1. The problem list of linear programming, each of which should be solved in the subsequent iterations.

2. The bottom bound of optimum value of the linear form of a problem .

On the first iteration as value of criterion function in any integer point undertakes . If a point to specify it is impossible, accept .

Let as a result iterations of a method have received the list from problems: and also exists . The algorithm of a BB method contains stages:

1 Stage. The problem for the decision gets out of the problem list of linear programming, . The problem is solved.

2 Stage. If problem has the decision we pass to a stage 3. Otherwise - we exclude problem from the list =. Transition to a stage 1. At we do a conclusion, that the initial problem has no decision and process of the decision comes to an end.

3 Stage. If we pass to a stage 4. Otherwise problem is excluded from the list. Transition to a stage 1.

4 Stage. If components of vector satisfy all to a integrity condition we pass to a stage 5. Otherwise problem R is excluded from the list. Plan is remembered. Transition to a stage 1. At vector is the decision of an initial problem and process of the decision comes to an end.

5 Stage. The problem is excluded from the list. The list joins two new problems of linear programming - the problem and the problem , =. Transition to a stage 1. Process of splitting of problem on two new problems of linear programming is carried out as follows.

Let - fractional a component in received optimum plan and the whole part. Then problem looks like:

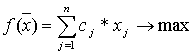
subject to

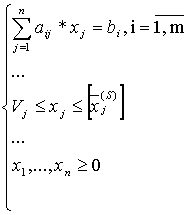(1)

Then problem looks like:

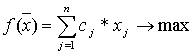
subject to

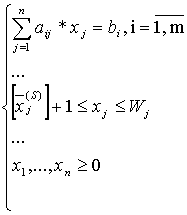(2)

Process of the decision proceeds will not be solved yet all of a problem of linear programming from the list. The decision of a problem will be on last iteration /2/.

Let's develop integer mathematical model of information system and we shall define the optimum decision by BB method.

The mathematical model is formulated as follows: from among the firms, rendering services satellite Internet in territory of the Russian Federation, it is required to choose the provider satellite Internet with the maximal size of the pure resulted effect (NPV) and satisfying to financial restrictions /3/.

Let - share of financing of the project NTV-plus, - share of financing of project Europe On Line, - share of financing of project Astra Network, - share of financing of project Satpro, - share of financing of project Network Service. - binary variables.

The integer mathematical model looks like.

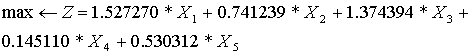
subject to (3)

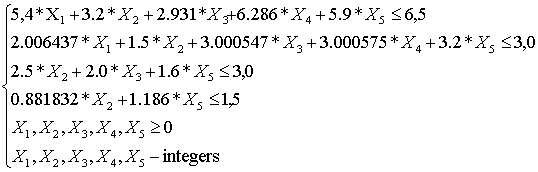
Let's solve a continuous problem. We shall lead to the standard form and we shall make the initial Jordan’s table (table 1).

Table 1

The initial Jordan’s table

БП	1	-	-	-	-	-
=	6.5	5.4	3.2	2.931	6.286	5.9
=	3.0	2.006437	1.5	3.000547	3.000575	3.2
=	3.0	0.0	2.5	2.0	0.0	1.6
=	1.5	0.0	0.881832	0.0	0.0	1.186
Z=	0	-1.52727	-0.741239	-1.374394	-0.14511	-0.530312

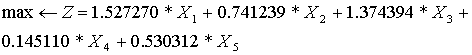
subject to (4)

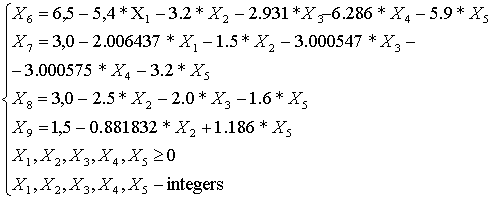
Iteration 1. Preliminary conditions: 1. The problem 1. 2. The bottom bound

.

Stage 1. We choose the task 1 and it is solved it. We receive the optimum plan (1,037635, 0, 0.305961, 0, 0), =2,00526.

Stage 2. The task 1 has the decision. Transition to 3 stage.

Stage 3. =2,00526>. Transition to 4 stage.

Stage 4. Variables have fractional values. Transition to 5 stage.

Stage 5. The task 1 is excluded from the list. The list joins two new problems: 2 and 3.

The admissible decision is resulted in table 2.

Table 2

The admissible decision

БП	1	-	-	-	-	-
=
=	0,58484	-0,371563	0,311	1,911498	0,664934	1,007782
=	3,0	0	2,5	2,0	0	1,6
=	1,5	0	0,881832	0	0	1,186
Z=	1,83838	0,282827	0,16381	-0,545426	1,632745	1,138371

The optimum decision of the continuous problem is resulted in table 3.

Table 3

The optimum decision of the continuous problem.

БП	1	-	-	-	-	-
=	1,037635	0,290692	0,504283	-0,283954	0,975263	0,806429
=	0,305961	-0,194383	0,1627	0,52315	0,34786	0,527221
=	2,388078	0,388766	2,174601	-1,0463	-0,69572	0,545558
=	1,5	0	0,881832	0	0	1,186
Z=	2,00526	0,176807	0,252551	0,28534	1,822477	1,425931

The problem 2.

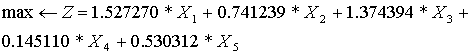
subject to (5)

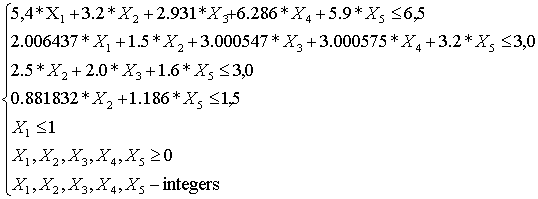
The problem 3.

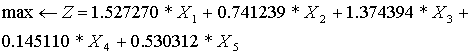
subject to (6)

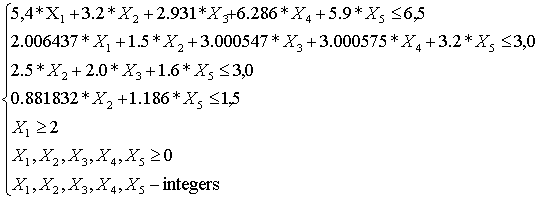
Optimum decision (1, 0, 0, 0, 0), =1,527270.

Results of the lead researches have allowed to draw following conclusions.

1. The integer mathematical model of optimization of the information system is developed, allowing to reduce expenses and terms of designing of information systems and to raise validity of accepted decisions.

2. The optimum decision of an integer problem of optimization of information system is found by the branch and bound method.

References:

1. Hamdy A Taha Operations Research: An Introduction. Seven Edition - М.: Publishing house "Williams", 2005 - 912 p.

2. Mastyaeva I.N., Gorbovtsov G.Y., Semenikhin O.N. Operations Research in economy: the Manual / the Moscow state university of economy, statistics and computer science. - М.: МSUESC, 2003. - 119 p.

3. Semakhin A.M. The analysis of mathematical model of information system. In the collection of materials X of the All-Russia scientifically-practical conference with the international participation (on November, 25-26th, 2011). - Tomsk: Publishing house of Tomsk university . Part 2 - 206 p.