Байджанов А.Р. , О.Г.Максимова
Череповецкий государственный университет
Компьютерное моделирование поведения проводимости сегнетоэлектрика.
Введение. Технический прогресс в области
вычислительной техники стимулировал развитие множества численных алгоритмов для
различных задач с использованием компьютеров. В итоге компьютерное
моделирование, наряду с традиционными теоретическими (аналитическими)
подходами, а также экспериментальными методами, превратилось в мощное средство изучения
свойств различных молекулярных систем и объектов. Сегнетоэлектрики, жидкие
кристаллы, полимерные вещества становятся все более важными для применения в
современной промышленности. При учете молекулярного строения таких систем можно
ожидать, что явления, происходящих в них, описываются весьма похожими методами,
поэтому становится очень актуальным вопрос о более глубоком изучении строения и
свойств этих веществ на уровне наноструктур (10-9 м).
Цель и задачи. Ключ для выяснения природы большинства
макроскопических природных явлений лежит именно в знании закономерностей
процессов, происходящих на атомно-молекулярном уровне. Целью данной работы
является создание компьютерной программы
для симуляции полной картины
поляризации сегнетоэлектрической системы и движения в ней заряженных
частиц с учетом всех особенностей протекания этих явлений. Были поставлены
следующие задачи:
1) Рассчитать конфигурацию положения диполей в
сегнетоэлектрике в зависимости от температуры, внутреннего строения (констант
потенциала межмолекулярного взаимодействия), внешнего электромагнитного поля.
2) Изучить движение заряженных частиц внутри
рассчитанной молекулярной системы.
3) Получить зависимости проводимости от внешних и внутренних характеристик.
Метод
решения. В качестве модели
сегнетоэлектрика принималась трехмерная решеточная модель, в каждой узле
которой находится анизотропная удлиненная частица (молекула) - диполь, обладающий
только вращательными степенями свободы [3]. Расчеты проводились в трехмерной
системе, вращение диполя вокруг его собственной
оси вращения не рассматривалось,
поэтому положение диполя характеризуется двумя сферическими углами – нутации ![]() и прецессии
и прецессии ![]() . В разработанной компьютерной программе конфигурация
системы описывалась двумя трухмерными массивами.
. В разработанной компьютерной программе конфигурация
системы описывалась двумя трухмерными массивами.
Конфигурация системы вычислялась с помощью
динамического метода Монте-Карло (алгоритм Метрополиса). На каждом шаге Монте -
Карло случайным образом выбирался диполь. Просчитывалась энергия его взаимодействия
с шестью ближайшими соседями и внешним электрическим полем. Далее диполь вращался случайным образом, и
снова вычислялась энергия взаимодействия. По значениям начальной и конечной
энергии определялось, применить ли последнюю конфигурацию. Новая конфигурация
принималась в том случае, если ее энергия меньше первоначальной или вероятность
перехода в новое состояние меньше случайного числа, выбранного в промежутке (0;
1). Вероятность перехода определяется с помощью формулы:
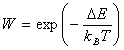
где W – вероятность перехода
диполя в новое состояние, ![]() - разность
значений энергии, Т – температура, kB – постоянная Больцмана.
Зависимость шагов Монте-Карло обратно пропорционатьно скорости нагревания или
охлаждения системы.
- разность
значений энергии, Т – температура, kB – постоянная Больцмана.
Зависимость шагов Монте-Карло обратно пропорционатьно скорости нагревания или
охлаждения системы.
|
|
|
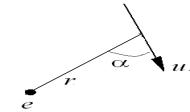
Рис.1. Потенциальная энергия взаимодействия электрона и
диполя |
Далее рассматривается
движение электронов, которое также рассчитывается методом Монте-Карло.
Потенциал взаимодействия между электроном и диполем определяется по формуле [1]:
![]()
где e - заряд электрона, u -
модуль дипольного момента, величины r и ![]() изображены
на рис. 1.
изображены
на рис. 1.
При моделировании
предполагалось, что электрон располагается в центре ячейки. Учитывались энергии
взаимодействия электрона с внешним электрическим полем и ближайшими восемью
диполями сегнетоэлектрика, а также взаимодействия диполей между собой. Координаты
электронов задавались так же случайным образом. Движение электрона основывалось
на проверке выгодности его положения в каждом из шести соседних мест: в
программе просчитывается энергия нахождения электрона во всех соседних ячейках
при варьировании его положения. Затем из массива полученных значений энергии
выбирается наивыгоднейшее положение и запускается процедура определения
вероятности перехода. Начальная и
конечная энергия сравниваются, и на основе этого выясняется, происходит или нет
переход электрона в соседнюю ячейку.
|
|
|
Рис. 2. Графическая визуализация движения электронов в
сегнетоэлектрической системе |
Следующий этап –
проверка, достиг электрон границы или
нет. Если ответ положительный, то
массив достигших границу увеличивается на единицу, а координаты электрона снова выбираются случайным образом.
Проводимость вычислялась как величина, пропорциональная количеству
заряженных частиц, прошедших через
заданную систему диполей за
определенное время.
На рис.2. изображена графическая визуализация конфигурации сегнетоэлектрика и движения электронов при температуре ниже точки
с фазового перехода (ориентация диполей имеет преимущественную ориентацию).
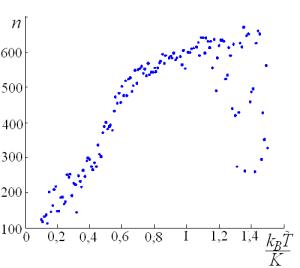
Результаты расчета. На рис.3 приведены
зависимости количество электронов, достигших левую границу сегнетоэлектрической
системы от величины ![]() , где K
– энергетическая константа взаимодействия между диполями. Так как число электронов, пересекающих
рассматриваемую ячейку, пропорционально проводимости, то по рис. 3 можно судить
о поведении восприимчивости сегнетоэлектрика при изменении температуры.
, где K
– энергетическая константа взаимодействия между диполями. Так как число электронов, пересекающих
рассматриваемую ячейку, пропорционально проводимости, то по рис. 3 можно судить
о поведении восприимчивости сегнетоэлектрика при изменении температуры.
|
|
|
Рис.3. Зависимости числа
электронов, достигших левую границу сегнетоэлектрической системы от величины |
Из рис.3а видно, что с увеличением температуры проводимость
возрастает вплоть до точки фазового перехода, которая была определена в работе
[2]. Такое поведение подтверждается также в экспериментальных работах В.В.
Кочервинского и С.Н.Дрождина.
Внешнее
электрическое поле нейтрализуется внутренним полем сегнетоэлектрической
системы, поэтому при низких температурах электрического тока не наблюдается. С
увеличением температуры поляризация системы уменьшается, поэтому количество
электронов, достигших левую границу, увелиличивается.
Литература:
1. М.Клеман, О.Д.Лаврентович. Основы физики частично упорядоченных сред. Москва :
Физматлит, 2007.
2. Настулявичус А.А.,
Баруздина О.С.,Павлова С.И. Изучение структуры молекулярного строения
сегнетоэлектриков методами компьютерного моделирования // Материали за VIII
международна научна практична конференция «Настоящи изследвания и развитие
-2012». 17-25 януари 2012. Т.10. с.85-88
3. Т.О.Петрова,
О.Г.Максимова, Р.А.Герасимов, А.В.Максимов. Применение аналитических и
компьютерных методов моделирования
систем с ориентационными взаимодействиями // ФТТ. 2012. Т.54. №5.с. 883-884.