Korzh R.A.

Krivoy Rog national university, Ukraine

HARMONIC, TIME-AMPLITUDE, FUNCTIONAL AND NOISED SOUND UNIT SUBMODEL DEVELOPMENT

Introduction

In audio signal processing techniques in terms of the theory of musical analysis and synthesis each sound unit is represented as an finite number of periods (stages) which determine its behavior at the specified moment of time [1].

Sub model development

Including the period structure with the main sound unit characteristics it is possible to extract the following sub models:

1. harmonic (timbre-associated);

2. time-amplitude;

3. functional;

4. noised.

Harmonic sub model represents the quality side of the sound unit object and shows the fundamental and partial tone distribution in the time-infinite oscillation process. The sub model uses the following parameters:

- fundamental frequency (f₀) (amplitude a₀ is assumed to be 1);

- frequency (f_i), amplitude (a_i) and phase () of the partials of the base tone.

So, the harmonic sub model is described as:

, (1)

which is clone of the sound unit timbre function [2].

Time-amplitude sub model shows the relative position and the mutual relationship of time (attack, hold, decay, sustain and release) to amplitude intervals. In other words, it determines the time-amplitude frames in which there are sound waves. The sub model uses the following parameters:

- time period moments (t_н, t_d, t_s, t_r);

- the base amplitude (a₀);

- advanced amplitude values (a_h, a_d, a_r) of the base amplitude.

So, the time-amplitude sub model is described as:

(2)

Functional sub model shows the time-amplitude form of the sound unit, limited by envelope functions on each time interval. The functions which set the advanced form of sound waves must be continuous within their ranges. The sub model uses the following parameters:

- time period moments (t_н, t_h, t_d, t_s, t_r, t_к);

- amplitude value for each period of time (a_max, a_dec, a₀, a_min);

- functional expression for each period of time (g_a(t), g_h(t), g_d(t), g_s(t), g_r(t)).

So, the functional sub model is describes as:

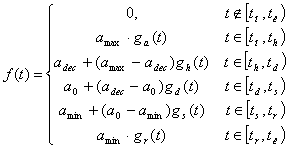(3)

Noised sub model shows the deviation and noise degree of the source sound wave form form the one which generates after the external noise component effect. The sub model uses the following parameters:

- sound unit equation u(t) [3];

- noise level (k);

- noise scheme S (additive/multiplicative).

So, the noised sub model is describes as:

(4)

All the previous information should be synthesized to get a compact functional expression which describes the separate sound unit [2]. Hence, we have the following formula:

(5)

Having (2.32), we can find the equation which describes the whole musical piece:

(6)

Plot analysis

Now let’s analyze plot dependencies on different parameters. Firstly, consider the effect of the amplitude on the total sound wave and its periods. Parameter a₀ shows value magnitude of the elastic body, which vibrates. The greater the scope, the stronger and louder the sound, and vice versa. Parameter a_max determines the maximum range within the parameter a₀:

(7)

Let f₀ = const = 1 Hz, = const = 1 s, and parameter a₀ make a variable, then we obtain the dependence of the hold period length on the sound vibration strength:

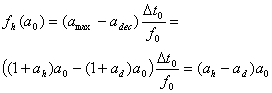(8)

Let value of a₀ in the range [0, 10], build a plot f_d(a) for different a_h and a_d (Fig. 1).

4

3

2

1

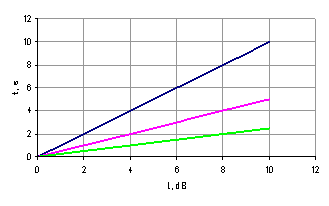
Figure 1 – Plot dependency of hold period from sound vibration strength

(1 – a_h = 1, a_d = 0; 2 – a_h = 1, a_d = 0,5; 3 – a_h = 0,6, a_d = 0,5; 4 – a_h = 0,5, a_d = 0,5)

Figure 1 shows that the maximal length of the holding period is reached when , and the minimal length when . Similarly, consider the dependence of the decay period length on the amplitude of the oscillations.

Let f₀ = const = 1 Hz, = const = 1 s, and parameter a₀ will be variable. As a result the following formula,

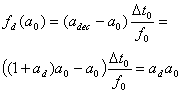(9)

4

3

2

1

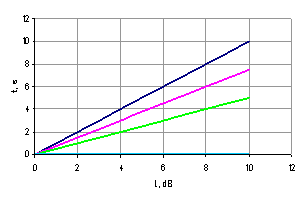
Figure 2 - Plot dependency of decay period from sound vibration strength

(1 – a_d = 1; 2 – a_d = 0,75; 3 – a_d = 0,5; 4 – a_d = 0)

is similar to the previous (8), we can see it from the plot f_d(a₀) of the decay period length on the amplitude a₀ for different a_d (Fig. 2).

Figure 2 shows that the maximal decay period length is reached when , and the minimal length when . Similarly, consider the dependence of the release period length on the amplitude of the oscillations.

Let f₀ = const = 1 Hz, = const = 1 s, and parameter a₀ will be variable. As a result the following formula:

(10)

4

3

2

1

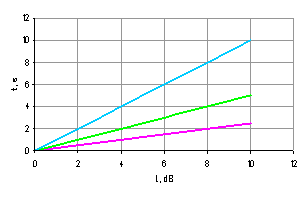
Figure 3 – Plot dependency of release period from sound vibration strength

(1 – a_r = 0; 2 – a_r = 0,5; 3 – a_r = 0,75; 4 – a_r = 1)

Let the values of a₀ in the range [0, 10], build a plot f_r(a₀) for different a_r (Fig. 3).

Figure 3 shows that the maximal release period length is reached when , and the minimal length when . And, finally, consider the dependence of the total time duration on the amplitude of the oscillations.

Let f₀ = const = 1 Hz, = const = 1 s, and parameter a₀ will be variable. As a result the following formula:

(11)

Let the values of a₀ in the range [0, 10], build the plot of f_total(a₀) for different a_h and a_r (рис. 4).

3

2

1

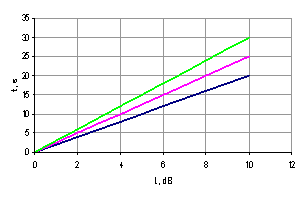
Figure 4 – Plot dependency of total time duration from sound vibration strength

(1 – a_h = 1, a_r = 0; 2 – a_h = 1, a_r = 0,5; 3 – a_h = 1, a_r = 1)

Figure 4 shows that the maximal duration is reached when , and the minimal duration when .

Conclusions

The plots describes above helped to determine the importance of the different quality characteristics of the sound wave unit structure. The future research is based on them and requires more complicated operations.

References:

1. Лэмб, Г. Динамическая теория звука. — Государственное издательство физико-математической литературы. — М. — 1995.

2. Голд, Б. Цифровая обработка сигналов (под ред. Трахтмана А. М.) / Б. Голд, Ч. Рэйдер. — М.: Советское радио. — 1973.

3. Корж Р. А. К проблеме автоматической идентификации музыкальных произведений / Р. А. Корж // Инженерия программного обеспечения. — №1 (9). — Киев. — 2012.

4. Яковлев А. Н. Введение в вейвлет-преобразования: учебное пособие / А. Н. Яковлев. — НГТУ, 2003. — 104 c.