Математика/1. Дифференциальные и интегральные уравнения

Супрунчук Т. А.

Брестский государственный университет имени А. С. Пушкина, Беларусь

Методика решения дифференциального уравнения методом

неопределенных коэффициентов

При использование метода неопределенных коэффициентов искомое решение подбирается в виде ряда .

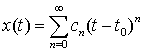Находятся производные ; все функции, входящие в дифференциальное уравнение раскладываются, в предположении, что они могут быть разложены, в степенные ряды по степеням . Полученные ряды подставляют в уравнение и находят неопределенные коэффициенты путем приравнивания выражений при одинаковых степенях в левой и правой частях уравнения. Кроме того, используются еще соотношения, учитывающие заданные начальные условия.

Алгоритм решения дифференциального уравнения методом

неопределенных коэффициентов

1. Записать искомое решение в виде степенного ряда

с неопределенными коэффициентами , Найти производные, входящие в дифференциальное уравнение, – получить выражения для производных в виде рядов, коэффициенты которых выразятся через ,

2. Разложить функции в степенные ряды по степеням .

3. Подставить полученные в пунктах 1, 2 выражения в заданное уравнение и прировнять коэффициенты при одинаковых степенях .

4. Используя начальные условия, решить полученную в пункте 3 систему относительно коэффициентов , , и выписать решение дифференциального уравнения.

Пример. Решить задачу Коши: , .

◄ 1. Будем искать решение в виде ряда 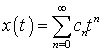, так как здесь начальное условие задано при . Тогда

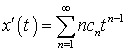или .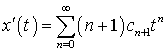

2. Функция представлена по степеням : .

3. Подставляя выражения для и в заданное уравнение, получаем равенство .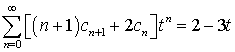

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях последнего равенства, получаем систему:

4. Из начального условия получаем , поэтому первые два уравнения системы дают , .

Для определения коэффициентов , , используя последнее уравнение системы, запишем . Заменив на , получим , Далее, заменив на , получим , и так далее. Таким образом,

.

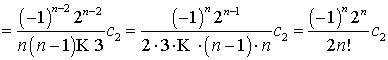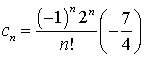Учитывая, что , окончательно получаем , . Таким образом, решение заданного уравнения можно записать в виде

.

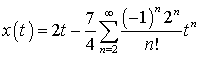Учитывая равенство 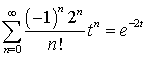, получаем окончательный ответ:

.

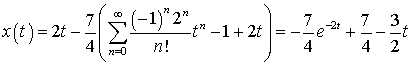Заметим, что заданное уравнение является простейшим линейным уравнением первого порядка. ►

Литература:

1. Наймарк, М. А. Линейные дифференциальные операторы/ М. А. Наймарк. – М.: Наука, 1969. – 528 с.