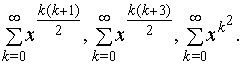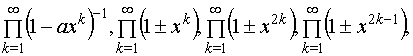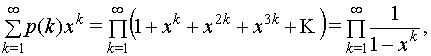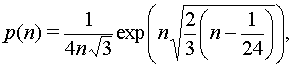К.ф.-м.н. Дикарева Е.В., к.ф.-м.н. Ситник С.М.

Воронежский институт МВД, Россия

Исторические сведения и некоторые приложения

тета-функций Якоби

 

Тета--функции являются одним из многочисленных примеров тех специальных функций, которые были по существу введены в математику великим Леонардом Эйлером, столетие которого было отмечено математическим сообществом в 2007 году. Список таких функций достаточно велик: гамма и бета--функции Эйлера, функции Бесселя, функция Ламберта, эллиптические интегралы, дзета--функция Римана, гипергеометрическая функция Гаусса, дилогарифмы Эйлера и полилогарифмы, функции разбиений, теоретико--числовая функция для количества взаимно--простых чисел с данным, многочлены Эйлера, и, наконец, тета--функции.

Тета--функции возникли в работах Эйлера в виде бесконечных произведений в связи с задачей о разбиении натурального числа на части. В этих работах Эйлер создал новые разделы математики: теорию производящих функций и --анализ на примере --гипергеометрических функций, к которым относятся ряды для тета--функций. По сути в этих работах в Анализ были впервые полноправно введены и функциональные бесконечные произведения, которые вместе с рядами и цепными дробями составляют три основные конструкции для представления функций в виде бесконечных выражений. Поэтому, не пытаясь принизить вклад в теорию тета--функций последующих математиков, среди которых были Аппель, Ватсон, Вейерштрасс, Гаусс, Гейне (или Хейне), Клейн, Коши, Кронекер, Лерх, Лиувилль, Пуассон, Рамануджан, Сельберг, Фурье, Цагир, Цвегерс, Эндрюс, Эрмит, Якоби, отмечаем, что возникновение этой теории относится к работам Леонарда Эйлера. Разумеется, наиболее полный анализ свойств тета--функций был проделан в работах немецкого математика Карла Густава Якоба  Якоби, в честь которого эти функции и были справедливо названы.

Первое упоминание о возможности рассматривать ряды, в которых степени идут не подряд, как в геометрической прогрессии, а по более сложным правилам с пропусками, встречается в работе Якоба Бернулли ещё в конце 17--го века, подобные ряды мы называем теперь лакунарными. Речь идёт о рядах вида 

                                                                    (1)

 Якоб Бернулли был замечательным учёным, некоторые его работы опередили своё время. Например, он первым построил решение для частного случая дифференциального уравнения, которое мы теперь называем уравнением Риккати . При этом искомая функция  записывалась им как частное двух рядов, по существу представляющих функции Бесселя с индексом одна треть, это и было первым упоминанием об этих функциях (а также и предвосхищением функций Эйри) [4-6]. Но в то время подобное бесконечное выражение, по--видимому, не считалось настоящим решением, в том числе и самим автором, и современники не обратили внимания на этот результат. Отметим, что и в дальнейшем теория функций Бесселя долго развивалась именно в связи с решением уравнения Риккати [2].

Эйлер в связи с задачами о разбиении натурального числа на части ввёл и изучил произведения вида 

                                 (2)

 разложения которых в ряды как раз и приводят к выражениям вида (1). Эйлер также ввёл и изучил производящую функцию для числа разбиений  натурального числа  в сумму натуральных слагаемых 

                              (3)

 а также различные варианты этой функции разбиений. Первые значения невелики , но с ростом  функция разбиений растёт довольно быстро и нерегулярно, например,  .

Тем удивительнее, что в двадцатом веке были найдены точные формулы для функции разбиений. Харди и Рамануджан нашли асимптотику этой функции 

                                                            (4)

 а затем и точную формулу в виде ряда с указанным первым членом, несколько начальных слагаемых которого уже позволяют вычислить точное значение . Первоначально в этой формуле под знаком корня в экспоненте стояло просто . Мистическое озарение, позволившее Рамануджану угадать добавку в минус 1/24, до сих пор вызывает чувство священного трепета. Ведь он располагал для анализа лишь совсем скудными числовыми данными. Удивительным является и применение дискретного преобразования Фурье с корнями 24 степени в этом ряде. Похоже, что с числом 24 у Рамануджана была особая связь (см. ниже про тау--функцию, введённую им для изучения представления натуральных чисел суммой 24 квадратов). Сама формула появилась в результате переоткрытия Рамануджаном в 1913 г. набора равенств, полученных ранее Роджерсом в 1894 г. и благополучно тогда всеми забытых, а теперь известных как тождества Роджерса--Рамануджана. Кстати, доказанные в 1934 г. знаменитым математиком Атле Сельбергом обобщения этих тождеств, также содержались в указанной статье Роджерса в эквивалентной форме.

Работы Эйлера по разбиениям были выполнены в основном в 1748 году и опубликованы в первой части его знаменитой трилогии по Анализу. На современном языке они содержали формулы для суммирования через тета--функции трёх базисных гипергеометрических рядов и были частными случаями так называемой

--биноминальной теоремы

                                      

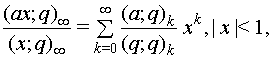
где использованы общепринятые сейчас обозначения

                  

Точнее, результаты Эйлера выражают ряды через бесконечные произведения и наоборот, подобные формулы были новыми в обе стороны. Отметим, что первые два примера Эйлера сразу следуют из --биноминальной теоремы, открытой намного позже Коши (1843 г.) и Гейне (1847 г.), при  значении , а для вывода третьего примера из этой теоремы потребовалось уже в точности ровно столетие (Коши, 1848 г.) и использование техники вычетов из теории функций комплексного переменного.

Тета--функции Якоби были первоначально определены и изучены им в работе "Fundamenta Nova Theoriae Functionum Ellipticarum", опубликованной в 1829 году в Кёнисберге. Этот город многим связан с историей математики, даже своими мостами (опять Эйлер!). Здесь Якоби в то время работал вместе с Бесселем, так как жизнь в столичном Берлине была очень дорогой (хотя отец Карла Якоби был обеспеченным человеком, семья потеряла средства во времена европейского финансового кризиса тех лет). Этот трактат содержал новый собственный подход Якоби, при котором теория всех эллиптических функций излагалась на основе введённых им тета--функций. Далее тета--функции были подробнейшим образом изучены им в ряде последующих работ, особенно в 1835--1838 годах. Широкую известность результаты Якоби получили в том числе в результате обработки и дополнений, выполненных его учеником Карлом Борхардом для издания лекций Якоби и собрания его сочинений. Следует отметить, что Якоби практически в одиночку построил основания теории тета--функций, что встречалось в истории математики  нечасто; так нами подсчитано, что из более чем сотни формул в соответствующей главе книги Уиттекера и Ватсона [5] только семь принадлежат другим математикам, а все остальные самому Якоби.

Тета--функции определяются при помощи быстро сходящихся тригонометрических рядов так [5-6]:

   

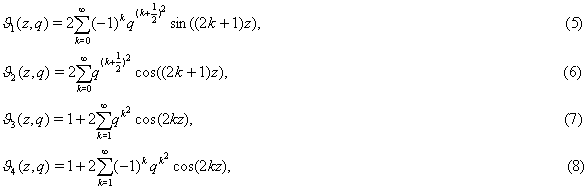
 где  (кстати, математический алфавит LaTeX'a, при помощи которого в этой фразе набирались бы символы числовых множеств,  называется Эйлеровым шрифтом). Данные обозначения, сохранившиеся неизменными и сейчас, также были введены Якоби, только  обозначалась им просто как , а вместо аргумента  выбиралось .  Эта система обозначений была выработана Якоби не сразу, в "Fundamenta Nova" применялись менее удобные обозначения, от которых он впоследствии отказался, хотя в некоторых современных книгах эти устаревшие обозначения продолжают приписывать ему как единственные.

В исследованиях Якоби по данному предмету важную роль сыграла его переписка с Адриеном--Мари Лежандром, общепризнанное главенство которого как основного эксперта того времени по теории специальных функций вообще и эллиптических функций в частности было неоспоримым. Следует отметить, что во времена Лежандра эллиптическими функциями назывались те из них, которые мы сейчас называем эллиптическими интегралами Лежандра трёх родов. Свои результаты в этой области, над которыми Лежандр работал около сорока лет, он изложил в итоговой знаменитой книге "Traite des Fonctions Elliptiques"], вышедшей в трёх томах с 1825 по 1830 годы. А современное определение эллиптической функции как мероморфной двоякопериодической начинается с работ Абеля. Между Якоби и Абелем, которые принадлежали к следующему за Лежандром поколению, развернулось неформальное соперничество за первенство в этой области, прерванное ранней смертью Абеля в 1829 году в возрасте 26 лет от нищеты, голода и туберкулёза. Лежандр не раз высказывал своё восхищение работами и Якоби, и Абеля: "...я узнал с таким же изумлением, как и удовлетворением, что двум молодым геометрам, Якоби в Кёнигсберге и Абелю в Христиании, удалось независимо друг от друга внести значительные усовершенствования в теорию эллиптических функций, причём в сложнейших её вопросах". Лежандр также проинформировал Якоби о письме Гаусса, в котором тот сообщал, что получил некоторые (многие?) из результатов Якоби и Абеля ещё в 1809 г., что подтвердилось после издания полного собрания трудов Гаусса в конце 19 века. А портрет Лежандра дополним таким штрихом: будучи небедным человеком, Лежандр предпочёл умереть в нищете, лишённый государством пенсии и других доходов. Причиной стал его отказ голосовать на выборах директора Национального Института за выдвинутого кандидатом чиновника--дебила из правительства (читатель может попробовать представить себе современного российского академика, отказавшегося голосовать на выборах в Академию за..., ну скажем, кандидатуру члена правительства, нам самим это представить как--то не получается). Таким был этот человек, "необыкновенно милый, но твёрдый как старые камни" (из письма Абеля).

Следует отметить роль Якоби и для развития теории эллиптических функций в России. Так его контакты с академиком Михаилом Васильевичем Остроградским и профессором математики Харьковского университета Матвеем Александровичем Тихомандрицким привели к написанию последним монографий, которые являются по--видимому одними из первых книг на русском языке (первыми?) по эллиптическим функциям. Отметим, что отечественные математики внесли весомый вклад в теорию эллиптических функций, в особенности в плане их применений для решения задач интегрирования функций.

Эрмит определил функции, зависящие от нескольких параметров, которые вводятся по формуле

 

                                              (5)

 При различных четырёх комбинациях параметров  получаются четыре функции Якоби. Кроме того, что функции Эрмита являются прямых многопараметрическим обобщением тета--функций Якоби, в их терминах единообразно, кратко и удобно записываются многие свойства самих тета--функций. Отметим, что  рассмотрены ещё более общие чем (9) функции вида 

                                             (6)

Свой оригинальный вариант обобщений тета—функций рассматривал и Рамануджан.

Приложения тета--функций многочисленны и разнообразны. Кратко обсудим некоторые из них.

Начнём с того интересного факта, что первое научное исследование Якоби состояло в попытках решить уравнение пятой степени в радикалах, так как результаты Галуа и Абеля в то время ещё не стали широко известными. Так вот, невозможное в радикалах в принципе решение алгебраических уравнений пятой и высших степеней оказывается возможным в терминах именно тета--функций! Однако разобраться в данном методе решения уравнения пятой степени, первоначально придуманном Шарлем Эрмитом ( отметим также в этом направлении работы Бринга, Кронекера, Клейна, Бриоски, Жубера, Вебера ), мягко говоря непросто, а решить им конкретное уравнение до конца по нашему мнению невозможно. Поэтому ни в одной из многочисленных книг и нет ни одного до конца решённого этим методом нетривиального уравнения, для которого были бы явно выписаны корни через тета--функции. Таким образом, данное направление по нашему мнению следует рассматривать как установившее принципиальную возможность разрешимости уравнений высших степеней в терминах специальных функций, а не как разумный практический способ такого решения. Например, во многих книгах приводится как образец знаменитое уравнение 

                                                                                       (7)

 для которого Абель, использовав предшествующие работы Руффини и Галуа, впервые доказал неразрешимость в радикалах, положив конец поискам общей формулы (это уравнение не стоит путать с похожим ). Но дальше этих сведений в книгах дело не идёт, даже для этого уравнения формулы для корней нигде не приводятся, только излагается общая методика решения. Отметим, что разрешимость в радикалах подобных трёхчленных уравнений, имеющих так называемую форму Бринга, была впоследствии полностью изучена Артуром Кэли и Дмитрием Александровичем Граве. Левые части подобных (11) уравнений иногда с издёвкой, но довольно метко называют малочленами].

Однако издавна существует альтернативная теория решения уравнений высших степеней в терминах гипергеометрических функций, которая широкому кругу специалистов практически неизвестна. В России этот подход разрабатывался в конце 19 века Леонидом Кузьмичём Лахтиным, ректором МГУ в 1904--1905 годах. Отметим в этом направлении недавнюю замечательную работу, в которой по существу предлагается явный доведённый до компьютерной программы алгоритм для решения уравнений пятой степени в терминах гипергеометрической функции . В том числе методами этих работ явно выписываются через гипергеометрические функции и решения уравнения (11), и более общего . Первым, насколько нам известно, начал применять гипергеометрические функции к решению уравнений пятой степени Феликс Клейн.

Далее, для алгебраического уравнения произвольной степени в 1980--ых годах японским математиком Хироси Умемурой была получена общая формула для корней. При этом корни оказываются выраженными через многомерные обобщения тета--функций на случай нескольких переменных: тета--константы, тета--функции Зигеля, гиперэллиптические интегралы (всегда обобщай!---Карл Якоби). Упомянутая работа не случайно была впервые опубликована как приложение к книге Д. Мамфорда "Лекции о тета--функциях".

Кроме быстро сходящихся тригонометрических рядов, существуют и другие методы вычисления тета--функций с фантастической скоростью сходимости. К ним относится метод арифметико--геометрического среднего Лежандра--Гаусса (AGM = arithmetic--geometric mean) или преобразование Ландена, на которых основаны современные рекорды по вычислению огромного количества знаков в различных системах счисления для числа . Отметим, что и в данном вопросе существенную роль играют классические и базисные гипергеометрические функции. Следует сказать, что заметную роль в пропаганде метода AGM и его развитии в конце 19 века сыграл уже упомянутый выше Карл Борхард--- один из учеников Якоби. Вот почему эффективные методы вычисления эллиптических функций основаны на их сведении к тета--функциям. Например, связь с полным эллиптическим интегралом Лежандра первого рода с параметром  выражается формулами 

                                                                                (8)

 Существует известный метод Вейерштрасса, позволяющий эффективно организовать вычисления по этим формулам с помощью быстро сходящихся рядов. Его суть состоит в удачном способе разрешить трансцендентное уравнение, составляющее второе из соотношений (12), то есть по данному  вычислить соответствующую величину , при этом не подсчитывая значения самих эллиптических интегралов. Через сами эллиптические интегралы от сопряжённых аргументов величина  выражается по формуле 

                                                                              (9)

 Более того, современные методы наиболее быстрого вычисления простейших элементарных функций, таких как экспонента, квадратный корень или синус с косинусом, также основаны на методе AGM, и, следовательно, используют всю мощь вычислительных алгоритмов для тета—функций . Это несколько напоминает ситуацию с современными оптимизированными алгоритмами для обычного умножения чисел, неожиданно основанными на быстром преобразовании Фурье (БПФ).

Тета--функции и другие эллиптические функции устанавливают связи q--анализа с квантовой физикой и теорией поля, например, посредством так называемых квантовых групп. Так стали называть после выступления В. Дринфельда в 1984 г. на семинаре И. М. Гельфанда те алгебры Хопфа, которые помогают решать уравнения Янга--Бакстера в квантовой теории поля. Заметный вклад в эту теорию внесла отечественная школа академика Л. Д. Фаддеева. Отметим, что Владимиру Дринфельду сделать доклад на международном конгрессе в Беркли в 1986 г. запретили, он стал Филдсовским медалистом на следующем конгрессе в Киото в 1990 г., а начал математические исследования ещё школьником, доказав одну из задач, относящихся к знаменитому неравенству Шапиро.

Рассмотрения в этой области начинаются с введённого, по--видимому, Херманом Вейлем обобщения понятия коммутативности: , где параметр ---некоторое число (или даже элемент поля). Например, подобному соотношению удовлетворяют простейшие операторы q--анализа: q--сдвиг и q--производная (на самом деле конечно--разностное отношение)

                          

Обычно рассматривается случай , но и случай  имеет приложения в физике, и им не стоит пренебрегать. Поэтому значения  будут нас особенно интересовать. Следует отметить, что некоторые конструкции q--анализа возникали ещё в работах Эйлера и Гаусса, но как самостоятельный раздел математики он оформился в основном в работах Хейнриха Эдуарда Хейне (или Гейне)---также ученика Якоби и участника его семинара для молодых математиков в Кёнигсберге. В дальнейшем развитие --анализа и теории базисных гипергеометрических функций было продолжено Роджерсом, Джексоном, Бейли, Ватсоном, Сирзом, Карлицем, Ханом, Слейтер, Агарвалом, Эндрюсом, Аски, Коорнвиндером, Вильсоном, Милном, Гаспером, Борвейном, Рахманом, Гельфандом, Граевым, Ретах, Зудилиным, Спиридоновым и многими другими. Моментом наивысшего торжества --анализа стало использование неотрицательности одного из вариантов базисных гипергеометрических функций---полиномов Аски--Вильсона---для завершающего шага в доказательстве знаменитой гипотезы Бибербаха в 1984 г. Луи де Бранжем .

Последнее время нам иногда кажется, что базисные гипергеометрические функции всё больше и больше вытесняют обычные классические как из теории, так и из приложений.

В теории дискретного преобразования Фурье (ДПФ) и его быстрых модификаций (БПФ) тета--функции нашли неожиданное применение при изучении спектральных и иных свойств этих преобразований. Самая первая задача спектрального анализа ДПФ, заключающаяся в описании спектра соответствующих матриц, была решена в начале 20--го века замечательным математиком Исайей Шуром, установившим волшебную связь размерностей собственных подпространств с величинами экспоненциальных квадратичных сумм, Кроме того, одна из дискретных конечномерных реализаций уравнения Шрёдингера записывается с помощью так называемой матрицы Харпера--Хофштадтера]. Решения системы уравнений с этой матрицей---функции Ахиезера--Бейкера, которые являются аналогами классических решений, ---также строятся с помощью тета--функций и их обобщений.

В настоящее время активно развивается такой раздел теории приближения функций, как аппроксимации с помощью целочисленных сдвигов Гауссовых экспоненциальных функций. Многие результаты этого направления отражены в недавней монографии Владимира Гилелевича Мазьи и Гюнтера Шмидта. Так вот, в этой теории алгоритмы разложения функций и анализа погрешностей основаны во многом на использовании тета--функций, на чём мы кратко остановимся в конце статьи. В качестве приложения данной разновидности интерполяции с использованием тета--функций строятся фильтры, характеристики которых близки к идеальным.

Стоит отметить, что на применении формулы Пуассона для тета--функции Риман основывал вывод функционального уравнения для дзета--функции Эйлера—Римана в своем знаменитом мемуаре 1859 года, положившем начало применению комплексного анализа для решения задач арифметики.

Совсем недавно произошёл долгожданный прорыв в развитии теории функций комплексного переменного для многосвязных областей; были получены результаты, основанные не на общей теории функций на многообразиях Римана, которые несмотря на их общность и красоту малоприменимы на практике, а на более—менее явных формулах для основных конформных отображений. Тета—функции играют заметную роль и в этой новой теории. В частности, через них выражается так называемая The Schottky-Klein prime function (главная функция Шоттки--Клейна), отвечающая за конформное отображение двусвязного кольца. В качестве приложений этой теории рассматриваются, например, гидродинамические задачи о течениях вдоль группы небольших островов, которые и играют роль внутренних компонент связности. Отличный обзор этой тематики представлен в недавней презентации  и имеющихся там ссылках.

Кроме того, в Анализе тета--функции используются при вычислении различных интегралов и их обращении как функций одного из пределов интегрирования. Многие задачи механики явно интегрируются в тета--функциях.

Рассмотрим задачи о представлении натуральных чисел в виде сумм нескольких квадратов чуть подробнее. Для двух квадратов имеется формула, которая эквивалентна тождеству для тета--функции Якоби в нуле, то есть в максимуме. Это тождество имеет вид

                          

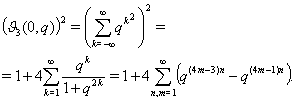
 Как следствие, справедлив следующий критерий. Пусть  - наивысшая степень простого числа р, на которую делится n. Для того чтобы n можно было представить в виде суммы двух квадратов, необходимо и достаточно, чтобы  было четным при .

Известная формула для числа представлений в виде суммы 4 квадратов эквивалентна знаменитому тождеству Якоби для тета--функции 

                                                      

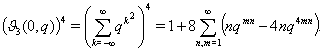
Это тождество можно сформулировать следующим образом: число представлений n в виде суммы четырех квадратов в восемь раз больше суммы всех делителей n, которые не делятся на четыре. Для всех нечетных n оно в восемь раз больше (а для четных n в 24 раза больше) суммы четных делителей n. Отсюда вытекает теорема Лагранжа: каждое целое n > 0 может быть представлено в виде суммы четырех квадратов.

Аналогичные по духу более сложные выражения для числа представлений суммой чётного числа квадратов получены до 24, во всех из них участвуют тета--функции. Разложения в сумму 24 квадратов описываются уже иначе устроенной функцией Рамануджана, которая определяется производящим соотношением

                                  

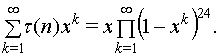
Что же касается представления суммой нечётного числа квадратов, то эта задача считается более трудной, некоторые результаты есть для 3 и 5 квадратов. Добавим, что Харди и Рамануджан нашли точные асимптотические формулы для числа представлений в виде k квадратов при .

Переходя к физическому примеру,  напомним, что осцилляции Блоха---это явление в физике твёрдого тела[1]. Это явление описывает осцилляции частицы (например, электрона) под действием электрического поля. При этом частица ускоряется и движется через периодический потенциал решётки кристалла. На стенках потенциальной ямы, наклон движения меняет свой знак. Поскольку наклон связан с групповой скоростью частицы, то направление её движения переходит в противоположное. Это и есть осцилляции частицы в потенциальной яме кристаллической решётки под действием внешней силы. Так вот оказывается, что волновые функции Блоха в случае потенциала, задаваемого по нормальному закону, выражаются по явной формуле через функцию .

Таким образом, нельзя не согласится с Полом Тураном, который предложил называть специальные функции другим термином---полезные функции!

Отметим, что различные неравенства для специальных функций родственных тета-функциям рассматриваются в работах [7-14]. дополнительные приложения тета-функций Якоби в различных задачах рассмотрены в работах [15-25].

 

Литература:

1.  Крылов А.Н. Леонард Эйлер. 1933.

2.  Юшкевич А.П. Леонард Эйлер. М., Знание, 1982.

3. Ситник С.М. Леонард Эйлер и теория специальных функций// Материалы Международной научной конференции "Леонард Эйлер и современная наука" (Санкт-Петербург, 15 - 18 мая 2007). Под ред. академика Ж.И. Алфёрова, ред.--состав. Л.И. Брылевская. Санкт-Петербург, 2007, С. 192--200.

4. Уиттекер Э.Т., Ватсон Дж.Н. Курс современного Анализа. Часть вторая. Трансцендентные функции. М., ГИФМЛ, 1963.

5.  Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т.3. М., Наука, 1967.

6.  Andrews G.E., Askey R., Roy R. Special functions. Cambridge University Press, 1999.

7.  Karp D., Sitnik S.M. Inequalities and monotonicity of ratios for

generalized hypergeometric function// Journal of Approximation Theory,

2009 , Volume 161, P. 337–-352.

8.  Karp D., Savenkova A., Sitnik S. M. Series expansions for the third incomplete elliptic integral via partial fraction decompositions //Journal of Computational and Applied Mathematics. 2007.---Vol. 207.---No. 2.---P. 331--337.

9. Karp D., Sitnik S. M. Asymptotic approximations for the first incomplete elliptic integral near logarithmic singularity // Journal of Computational and Applied Mathematics.---2007.---Vol. 205.---P. 186--206.

10. Karp D., Sitnik S. M. Inequalities and monotonicity of ratios for generalized hypergeometric function // Arxiv: math. CA/0703084.---2007.---14 P.

11.  Karp D., Sitnik S. M. Two-sided inequalities for generalized hypergeometric function // RGMIA Research Report Collection.---2007.--- 10(2).---Article 7.---14 P.

12.  Karp D., Sitnik S. M. Asymptotic approximations for the first incomplete elliptic integral near logarithmic singularity // 2006.---Arxiv: math. CA/0604026.---20 P.

13.  Karp D., Savenkova A., Sitnik S. M. Series expansions and asymptotics for incomplete elliptic integrals via partial fraction decompositions // Proceedings of the fifth annual conference of the Society for special functions and their applications (SSFA).---2004.---Lucknow (India).---P. 4--30.

14. Ситник С. М. Неравенства для полных эллиптических интегралов Лежандра //  Препринт ИАПУ ДВО РАН.---Владивосток, 1994.---17 С.

15.  Lanzara F., Maz’ya V. and Schmidt G. Approximate Approximations from Scattered Data / F. Lanzara, V. Maz’ya, G. Schmidt / J. Approx. Th., 2007, 145, p. 141-170.

 16. Maz’ya V., Schmidt G. On approximate approximations using Gaussian kernels/ V. Maz’ya, G. Schmidt / IMA J. Num. Anal., 1996, 16, p. 13-29.

 17. Maz’ya V., Schmidt G. Approximate approximations/  V. Maz’ya,  G. Schmidt – University of Linköping, Sweden, 2007 – 350 p.

18. M. V. Zhuravlev, E. A. Kiselev, L. A. Minin and S. M. Sitnik. Jacobi theta-functions and systems of integral shifts of Gaussian functions/ Zhuravlev  M. V.,  Kiselev E. A., Minin  L. A., Sitnik  S. M. / Journal of Mathematical Sciences, Springer, 2011, Volume 173, Number 2, p. 231-241.

19. Журавлёв М.В., Киселёв Е.А., Минин Л.А., Ситник С.М. Тета--функции Якоби и системы целочисленных сдвигов функций Гаусса/ М.В. Журавлёв, Е.А. Киселёв, Л.А. Минин, С.М. Ситник /Современная математика и её приложения. Т. 67. Уравнения в частных производных.  2010,  c. 107-116.

20. Минин Л.А., Ситник С.М., Журавлев М.В. О вычислительных особенностях интерполяции с помощью целочисленных сдвигов гауссовых функций. / М.В. Журавлёв, Л.А. Минин, С.М. Ситник / Научные ведомости Белгородского государственного университета. 2009, № 13 (68), Выпуск 17/2, с. 89-99.

21. Минин Л.А., Ситник С.М. О неравенствах для тета-функций Якоби/ Л.А. Минин, С.М. Ситник / Чернозёмный альманах научных исследований. Серия "Фундаментальная математика". 2009, №1 (8), c. 234-311.

22. Минин Л.А. Ситник С.М. Неравенства для третьей тета-функции Якоби/ Л.А. Минин, С.М. Ситник / Материалы Всероссийской заочной научно--практической конференции "Современная математика и проблемы математического образования". Орёл, Орловский государственный университет, 2009, c. 61-68.

23. Минин Л.А., Ситник С.М. Неравенства для третьей тета-функции Якоби/ Л.А. Минин, С.М. Ситник / Аналитические методы анализа и дифференциальных уравнений (АМАДЕ). Тезисы докладов международной конференции. 2009, Минск, Беларусь. с. 111.

24. Минин Л.А., Ситник С.М. О неравенствах для тета-функций Якоби/ Л.А. Минин, С.М. Ситник / Труды участников международной школы –семинара по геометрии и анализу памяти Н.В. Ефимова. Абрау-Дюрсо, 2008, Ростов-на-Дону, Южный Федеральный университет, 2008. с. 124-126.

25. Ситник С.М., Тимашов А.С. Применение экспоненциальной интерполяции в задачах сжатия и хранения информации/ Ситник С.М., Тимашов А.С. / Сборник материалов 2 всероссийской научно-технической конференции с международным участием «Информтех-2012» Курск Юго-западный государственный университет, 2012 с. 50-59.

 

 


[1] Феликс Блох---немецкий физик, нобелевский лауреат 1959 года "за развитие новых методов для точных ядерных магнитных измерений и связанные с этим открытия", один из создателей метода ЯМР--томографии, широко применяемого в современной медицине.