Копжасарова А.А.
Докторант
Phd, ЮКГУ им. М.Ауезова
О базисности Рисса собственных функций в случае ![]() ,
, ![]() .
.
Рассмотрим
обобщенную спектральную задачу [1]
![]() (1)
(1)
![]() (2)
(2)
в
случае ![]() ,
, ![]() обладают «хорошими
спектральными свойствами».
обладают «хорошими
спектральными свойствами».
Теорема 1. Система собственных
функций краевой задачи (1), (2) в случае ![]() ,
, ![]() образует базис Рисса в пространстве
образует базис Рисса в пространстве ![]() .
.
Доказательство. Так как по условию регулярности ![]() то не уменьшая общности можно
положить
то не уменьшая общности можно
положить ![]() . Тогда краевые условия (2) примут вид
. Тогда краевые условия (2) примут вид
![]() (3)
(3)
Найдем собственные значения и собственные
функции этой задачи. Линейно независимыми решениями уравнения (1)
являются функции
![]() .
.
Поэтому общее решение
уравнения (1) имеет вид
![]() . (4)
. (4)
Удовлетворяя функцию (4) краевому условию (3),
для нахождения неизвестных коэффициентов ![]() и
и ![]() получаем систему
получаем систему
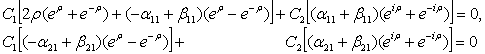 (5)
(5)
Так
как мы ищем собственную функцию задачи (1), (3), то ![]() . [2] Поэтому хотя бы один из коэффициентов
. [2] Поэтому хотя бы один из коэффициентов ![]() или
или ![]() должен быть отличным
от нуля. Следовательно, система (5), рассматриваемая как линейная
алгебраическая система относительно неизвестных
должен быть отличным
от нуля. Следовательно, система (5), рассматриваемая как линейная
алгебраическая система относительно неизвестных ![]() и
и ![]() , должна иметь ненулевое решение. Это эквивалентно равенству
нулю определителя системы (5):
, должна иметь ненулевое решение. Это эквивалентно равенству
нулю определителя системы (5):
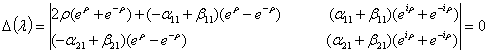 .
.
Выделяя из
второго столбца определителя общий множитель, получаем
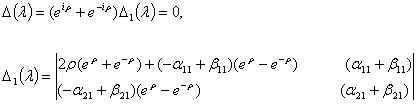 (6)
(6)
Равенство
нулю определителя ![]() означает, что либо
означает, что либо ![]() , либо
, либо
![]() . Рассмотрим
сначала первое равенство.
. Рассмотрим
сначала первое равенство.
Если ![]() то корни этого
уравнения могут быть вычислены точно и равны
то корни этого
уравнения могут быть вычислены точно и равны ![]()
Поэтому
первая серия собственных значений задачи (1), (3) имеет вид
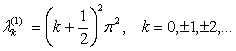 (7)
(7)
Рассмотрим
теперь второй случай. Пусть ![]() .
Тогда после элементарных преобразований получаем
.
Тогда после элементарных преобразований получаем
![]() .
.
Здесь

Далее, это уравнение
эквивалентно следующему:
![]() (8)
(8)
С применением теоремы
Руше, находим
![]() (9)
(9)
Поэтому
вторая серия собственных значений задачи (1), (3) имеет вид
![]() (10)
(10)
Найдем
теперь собственные функции задачи (1), (3), соответствующие
собственным значениям ![]() и
и ![]() .
.
Для собственных значений ![]() и
и ![]() соответствующие
собственные функции имеет такого вида
соответствующие
собственные функции имеет такого вида
![]()
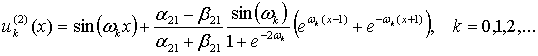 (11)
(11)
При этом
![]() ;
;  (12)
(12)
Построим
теперь систему функций, биортогонально сопряженную системе ![]() . Для этого рассмотрим задачу, сопряженную краевой задаче (1), (3). Стандартными вычислениями находим, что задачей сопряженной к задаче (1), (3) является следующая краевая задача:
. Для этого рассмотрим задачу, сопряженную краевой задаче (1), (3). Стандартными вычислениями находим, что задачей сопряженной к задаче (1), (3) является следующая краевая задача:
![]() (13)
(13)
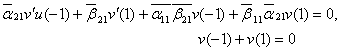 (14)
(14)
В силу сопряженности задач, собственными значениями
сопряженной задачи будут ![]() и
и ![]() . [3] Соответствующие им собственные функции сопряженной
задачи имеет вид
. [3] Соответствующие им собственные функции сопряженной
задачи имеет вид
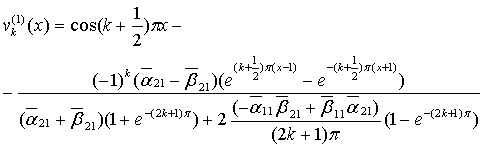 (15)
(15) 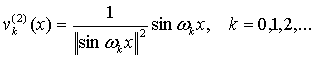 . (16)
. (16)
Тем самым
нами полностью вычислены собственные значения двух сопряженных задач (1), (3)
и (15), (16) и соответствующие им собственные функции. Для
доказательства базисности Рисса в L2(-1,1) полученных систем функций ![]() и
и ![]() воспользуемся
критерием базисности Рисса
воспользуемся
критерием базисности Рисса
![]() ,
, ![]() (17)
(17)
![]() (18)
(18)
систем
собственных функций оператора, порожденного выражением (1) и регулярными (но не
усиленно регулярными) краевыми условиями .
Для этого
оценим нормы найденных нами собственных функций.
Из представления (12)
находим, что
![]()
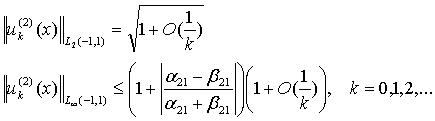 (19)
(19)
Для норм
собственных функций сопряженной задачи (13), (14) проводим
аналогичные вычисления. Из
представления (15) находим, что
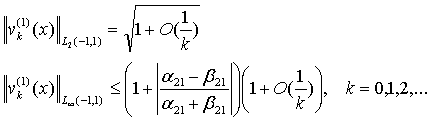 (20)
(20)
Для второй серии
собственных функций имеем из (16):
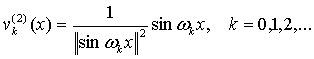 .
.
С учетом асимптотики ![]() нетрудно убедиться в
том, что
нетрудно убедиться в
том, что
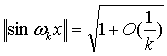 .
.
Поэтому
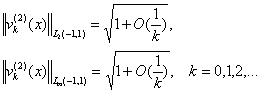 (21)
(21)
Теперь из
полученных неравенств (19)-(21) легко убеждаемся в выполнении неравенств (17),(18).
Тем самым найденные системы собственных функций ![]() и
и ![]() удовлетворяют всем
требованиям базисности Рисса. Следовательно системы
собственных функций
удовлетворяют всем
требованиям базисности Рисса. Следовательно системы
собственных функций ![]() и
и ![]() образуют базисы Рисса
в пространстве
образуют базисы Рисса
в пространстве ![]() .
.
Литература
1. Като Т.
Теория возмущений линейных операторов М.,1972.
2. Наймарк М.А. Линейные
дифференциальные операторы. М., 1969.
3.Тенгаева А.А. Об условиях базисности систем собственных
функций обобщенных спектральных задач для обыкновенных дифференциальных
уравнений: дис. … канд. физ.-мат.наук.- Алматы,
2010. - С.52-63.