Абдрахманов
Р.Б.
Худайберганов С.
Абдурахманов
С.
Международный казахско-турецкий
университет имени Х.А.Ясави, г.Туркестан
Tашкентский
государственный технический университет имени А.Р.Беруни, г. Ташкент
ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЕ ТИПА ФРЕДГОЬМА
Многие задачи физики и
прикладной математики приводиться к решению интегральному уравнению следующего
типа.
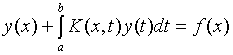 (1)
(1)
здесь ![]() и
и ![]() -известные функции. Предположим для этого интегрального уравнение выполнены все условии
существование решений. Разбиваем
отрезок [а,b] на n частей точками
-известные функции. Предположим для этого интегрального уравнение выполнены все условии
существование решений. Разбиваем
отрезок [а,b] на n частей точками ![]() и назовём решением интегральной
уравнение (1) значении неизвестной функции в этих точках т.е
и назовём решением интегральной
уравнение (1) значении неизвестной функции в этих точках т.е ![]() . Введем обозначения:
. Введем обозначения: ![]() ,
, ![]() , далее заменяя в уравнение (1) интеграл интегральной
суммой получим систему алгебраических уравнений относительно неизвестных
, далее заменяя в уравнение (1) интеграл интегральной
суммой получим систему алгебраических уравнений относительно неизвестных ![]() .
.
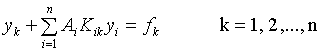 (2)
(2)
где ![]() - известные коэффициенты, зависящий от выбора метода замены интеграла на интегральную
сумму.
- известные коэффициенты, зависящий от выбора метода замены интеграла на интегральную
сумму.
Решая систему линейных алгебраических уравнений (2)
известными методами получим решение уравнений (1). Для решения этой системы
составлена программа на алгоритмическом языке Паскал. Ниже приводится тестовый
пример.
Пример. Очевидно точным решением интегрального уравнение
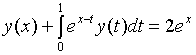
является
функция ![]() . В таблице приведена точная и приближенная решения
уравнение.
. В таблице приведена точная и приближенная решения
уравнение.
|
|
|
|
|
0.0 |
0,999999999 |
1,0000000 |
|
0.1 |
1,105170918 |
1,105170918 |
|
0.2 |
1,221402758 |
1,221402758 |
|
0.3 |
1,349858808 |
1,349858808 |
|
0.4 |
1,491824698 |
1,491824698 |
|
0.5 |
1,648721271 |
1,648721271 |
|
0.6 |
1,822118801 |
1,8221188 |
|
0.7 |
2,013752707 |
2,013752707 |
|
0.8 |
2,225540928 |
2,225540928 |
|
0.9 |
2,459603111 |
2,459603111 |
|
1.0 |
2,718281828 |
2,718281828 |
Литература
1.
Вольмир А.
С. "оболочки в потоке жидкости и газа: задачи аэроупругости " М.
Наука, 1976 г. 416с.
2.
Гроссман Е. П. "Курс вибраций частей самолета" М.
оборонгиз,1940 310с.
3.
Бадалов Ф. Б. "Методы решения интегральных и
интегродифференциальных уравнений наследственной теории вязко упругости".
Ташкент. "Мехнат" 1987. 269 с.
4.
Денисов Г. Г., Новиков В. В. О влиянии внутреннего трения на
устойчивость одномерных упругих систем. Сб. "Динамика систем". изд
Горьковского ун-та. 1975.