Листопадова В.В.

Национальный технический университет Украины «КПИ»

КРУГЛАЯ ПЛАСТИНА В АКУСТИЧЕСКОЙ СРЕДЕ. СТАЦИОНАРНАЯ ЗАДАЧА

Механическую модель прохождения звука через круглую пластину представим следующим образом.

Пусть с левой (лицевой) стороны пластины падает плоская монохроматическая волна давления в направлении нормали к фронту. Падающую, дифракционную и прошедшую волны обозначим соответственно цифрами 1, 2 и 3. Толщину пластины примем равной , а радиус – .

Систему координат свяжем со срединной плоскостью, а точку совместим с геометрическим центром пластины.

Очевидно, что она наиболее подвержена влиянию акустического излучения в направлении нормали к поверхности, так как именно здесь ее импеданс минимальный по сравнению с двумя другими измерениями.

Проанализируем возмущенное изгибное движение торцевой пластины поплавка под действием плоской звуковой волны.

Дифференциальное уравнение вынужденных колебаний в форме Софи Жермен имеет вид –

, (1)

где – итерированный лапласиан (бигармонический оператор); , , и – цилиндрическая жесткость, плотность материала пластины, толщина и коэффициент Пуассона соответственно.

Пластина колеблется относительно плоскости . Уравнение (1) справедливо в плоской области , которая расположена в системе . Решения ищем для .

Это уравнение дает удовлетворительные результаты, если отношение толщины пластины к наименьшей длине генерируемой волны не превышает 0,1. В противном случае следует учитывать сдвиг и инерцию вращения, либо решать трехмерную задачу.

Стационарная задача.

Исключим из рассмотрения время и установим закономерность распространения акустической вибрации. В этом случае уравнение (1) преобразуется к виду –

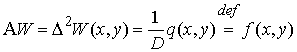, (2)

где - проекция плотности возмущающей силы на нормаль к лицевой поверхности.

На боковой поверхности пластины

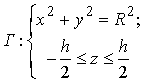(3)

выполняются граничные условия первого рода

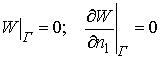, (4)

что соответствует жесткому закреплению. Символом обозначена внешняя нормаль к боковой поверхности.

Построим систему линейно независимых функций

(5)

принадлежащих области определения бигармонического оператора и удовлетворяющих условиям (3). Назовем их координатными. Их линейную оболочку обозначим через . Таким образом, координатные функции образуют базис

в своей линейной оболочке .

Найдем приближенное решение задачи (2) … (4) в виде линейной комбинации координатных функций

(6)

со столбцом

(7)

неизвестных коэффициентов , подлежащих определению. Тогда выражение (6) приводит к следующему приближенному равенству –

. (8)

Укажем наилучший выбор столбца .

Обозначим

(9)

и назовем эти функции образами координатных функций . Линейную оболочку образов обозначим через и отметим, что

. (10)

Вначале докажем, что образы координатных функций также линейно независимы и, следовательно, образуют базис в .

С этой целью построим нулевую линейную комбинацию образов координатных функций –

.

Известно, что оператор положительно определен на классе функций, которые удовлетворяют граничным условиям (4), что означает

,

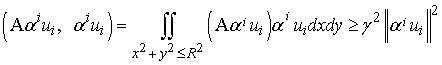где – постоянная, не зависящая от . Отсюда

.

Но координатные функции линейно независимы, поэтому

,

что означает линейную независимость функций , значит они образуют базис

,

в своей линейной оболочке .

Из соотношений (8), (9) следуют приближенные равенства –

(11)

Наилучшим считается такой столбец , при котором

(12)

Это условие представляет собой один из вариантов классической идеи, восходящей к ld. Rayleigh, В. Ритцу, И.Г. Бубнову, С.П. Тимошенко, Б.Г. Галеркину.

Выберем в качестве координатных функций следующие:

(13)

Они безразмерны, принадлежат области определения бигармонического оператора , а также удовлетворяют граничным условиям.

Образы этих функций определяются соотношениями:

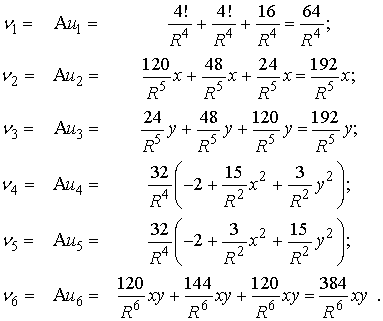(14)

Остается вычислить элементы матрицы Грама образов координатных функций –

.

В окончательном виде матрица Грама будет представлена в виде –

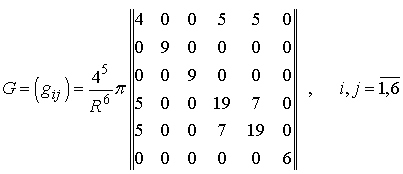. (15)