Ковалець О.Я.
Национальный
технический университет Украины «КПИ»
ПЛАСТИНИ ОБМЕЖЕНОЇ
ПРОТЯЖНОСТІ
Проходження
акустичних хвиль крізь плоскі перешкоди у вигляді нескінченних пластин
описується суттєво спрощеним математичним апаратом і значно знижує трудоємність
аналізу. Для вивчення окремих питань цього цілком достатньо і часто-густо
такими моделями обмежується вивчення динаміки пружної взаємодії плоских
перешкод із акустичною хвилею.
Разом з
тим, імітаційне (наближене) моделювання процесу призвело, як з’ясувалося, до
спрощень, за яких результати теоретичних і експериментальних досліджень стали
призводити до не погоджених між собою висновків. В першу чергу це стосується
прояву локальних особливостей.
Вихід
із ситуації полягає в максимальному наближенні імітаційних механічних і
математичних моделей до реальних. Стосовно вивчаємих задач – це вимагає
переходу від нескінченних пластин до пластин обмежених розмірів.
Аналіз
згинних коливань плоских тіл обмежених розмірів ефективно проводиться шляхом
представлення збурення та прогину пластини подвійним рядом в прямокутній
області. Цей метод має найбільш просту математичну інтерпретацію, але дозволяє,
разом з цим, досить глибоко вивчати динаміку тіл обмежених розмірв.
Скористуємося
ним для подальшого.
Розглянемо
двовимірну задачу. Припустимо, що довжина пластини дорівнює ![]() , ширина –
, ширина – ![]() , товщина –
, товщина – ![]() і стала на всій
площині. Вважаємо також, що товщина набагато менша інших розмірів, тобто
і стала на всій
площині. Вважаємо також, що товщина набагато менша інших розмірів, тобто
![]() ;
; ![]() .
.
Матеріал
пластини приймаємо абсолютно пружним, однорідним та ізотропним на всій площині.
Довжину згинної хвилі вважаємо більше ніж у шість раз перевищуючою товщину, що
дає можливість використовувати рівняння тонкої пластини.
Акустичне
поле приймається дифузним.
За
введених обмежень, можна стверджувати, що бічні грані виділеного елементу
площини довжини ![]() і ширини
і ширини ![]() за весь час руху
залишаються паралельними площинам
за весь час руху
залишаються паралельними площинам ![]() та
та ![]() і перпендикулярними
до серединної площини (рис. 1).
і перпендикулярними
до серединної площини (рис. 1).
Якою б
функцією координат ![]() ,
, ![]() не був прогин
не був прогин ![]() пластини, його завжди
можна навести в прямокутній області подвійним рядом за нормальними функціями,
тобто
пластини, його завжди
можна навести в прямокутній області подвійним рядом за нормальними функціями,
тобто
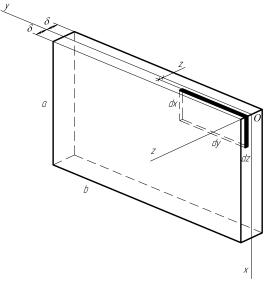
Рис. 1. Схема просторового навантаження пластини
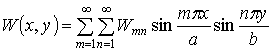 , (1)
, (1)
де ![]() ,
, ![]() – числа напівхвиль
згину відповідно вздовж осей
– числа напівхвиль
згину відповідно вздовж осей ![]() та
та ![]() ;
; ![]() – зміщення точки
поверхні пластини з координатами
– зміщення точки
поверхні пластини з координатами ![]() ,
, ![]() в напрямку
в напрямку ![]() ;
; ![]() (рис. 7).
(рис. 7).
Легко
бачити, що кожен член ряду (1) задовольняє граничним умовам виду
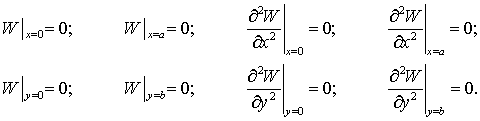 (2)
(2)
З
огляду на вираз (31), можна обчислити максимальну потенційну енергію ![]() , що накопичується при згинній деформації.
, що накопичується при згинній деформації.
З цією метою, достатньо означити
максимальне значення потенціальної енергії ![]() елементарної ділянки
(рис. 1), а потім одержаний вираз зінтегрувати у двох
напрямках:
елементарної ділянки
(рис. 1), а потім одержаний вираз зінтегрувати у двох
напрямках:
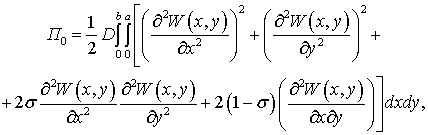 (3)
(3)
де ![]() – циліндрична
жорсткість поверхні пластини;
– циліндрична
жорсткість поверхні пластини; ![]() – модуль пружності;
– модуль пружності; ![]() – коефіцієнт Пуасона.
– коефіцієнт Пуасона.
Величина максимальної кінетичної енергії ![]() поперечних коливань
пластини обчислюється за формулою
поперечних коливань
пластини обчислюється за формулою
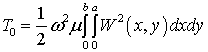 , (4)
, (4)
де ![]() – питома маса;
– питома маса; ![]() – колова частота.
– колова частота.
Застосуємо загальне рівняння динаміки для побудови
диференціального рівняння пластини в головних координатах. Одержуємо:
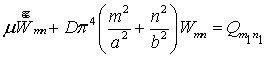 ,
(5)
,
(5)
де 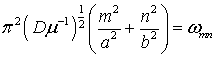 – власна частота
коливань;
– власна частота
коливань; ![]() – узагальнена
– узагальнена
Рис. 2. Розподіл прогинів пластини: m, n –
числа на півхвиль
сила, яка містить той фізичний зміст, щоб добуток ![]() являв собою
віртуальну роботу, а чисельно сила
визначається як коефіцієнт при варіації узагальненої координати
являв собою
віртуальну роботу, а чисельно сила
визначається як коефіцієнт при варіації узагальненої координати ![]() .
.
Отже, якщо падаючу звукову хвилю ![]() навести у вигляді
навести у вигляді
![]() ,
(6)
,
(6)
де ![]() – амплітуда тиску
відповідної форми і
– амплітуда тиску
відповідної форми і ![]() ,
, ![]() – числа напівхвиль
звукового тиску, які приходяться на довжину і ширину, тоді її віртуальна робота
обчислюється з формулою
– числа напівхвиль
звукового тиску, які приходяться на довжину і ширину, тоді її віртуальна робота
обчислюється з формулою
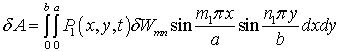 .
(7)
.
(7)
Приймаємо для конкретності
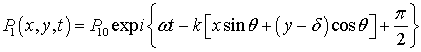 , (8)
, (8)
де ![]() – амплітуда тиску;
– амплітуда тиску; ![]() – хвильове число.
Тоді, з виразу (7) походить, що
– хвильове число.
Тоді, з виразу (7) походить, що

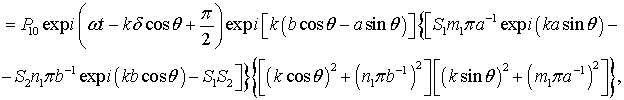 (9)
(9)
де ![]() ;
; ![]() .
.
У тому випадку, коли ![]() ,
, ![]() , що відповідає рівномірно розподіленому навантаженню на всю
площину, формула (9) перетворюється на таку:
, що відповідає рівномірно розподіленому навантаженню на всю
площину, формула (9) перетворюється на таку:
![]() (10)
(10)
Поза сумніву, що для парних значень величин ![]() та
та ![]() узагальнена сила
дорівнює нулю, тобто:
узагальнена сила
дорівнює нулю, тобто:
![]() . (11)
. (11)
Навпаки, для непарних значень –
![]() . (12)
. (12)
Обчисливши тепер максимальну
роботу ![]() , яку виконує падаюча хвиля звукового тиску, за формулою
, яку виконує падаюча хвиля звукового тиску, за формулою
 , (13)
, (13)
можна встановити закон згинних коливань пластини
виходячи з умови екстремальних її властивостей при згині:
 . (14)
. (14)
За необхідності врахування
дисипації енергії, обумовленої
внутрішнім тертям, досить у виразі (14)
прийняти до уваги роботу цих сил –
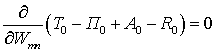 , (15)
, (15)
де
 ; (16)
; (16)
![]() – коефіцієнт
внутрішнього тертя;
– коефіцієнт
внутрішнього тертя; ![]() – коефіцієнт втрат.
– коефіцієнт втрат.