Педагогічні науки / 5. Сучасні методи викладання

К.п.н. Ачкан В.В.

Бердянський державний педагогічний університет

Посилення прикладної спрямованості навчання у процесі вивчення похідної та інтрегралу у класах економічного профілю

В умовах реформування освіти України, впровадження компетентнісного підходу у навчання, профілізації старшої школи орієнтованість навчання на дитину, на світ, який її оточує, на її повсякденне життя є найважливішим завданням освіти. Тому теза “математику треба вчити так, щоб вміти її застосовувати”, яку висловлювали відомі математики і педагоги, зокрема,
В.І. Арнольд [1] є актуальною для вітчизняної школи. Про це свідчать і результати міжнародних порівняльних досліджень, які проводяться в останні десятиріччя. Вони показали, що українські школярі краще, ніж учні багатьох країн світу, виконують завдання репродуктивного характеру, які відображають оволодіння предметними знаннями та вміннями. Але їхні результати нижчі при виконанні завдань на застосування знань у практичних, життєвих ситуаціях, зміст яких подано в незвичній, нестандартній формі; в яких потрібно провести аналіз даних або їх інтерпретацію, сформулювати висновки. Тому посилення прикладної спрямованості навчання математики, особливо у старшій школі в контексті її профілізації є актуальною та важливою проблемою.

Одними з основних розділів шкільного курсу алгебри і початків аналізу є розділи “Похідна та її застосування” та “Інтеграл та його застосування”. Ці розділи є складовою частиною змістової лінії функція і мають розгалужену систему внутрішньо-предметних (з іншими лініями курсу) та міжпредметних зв’язків. До того ж ці розділи отримують своє логічне продовження у курсі математики у ВНЗ. Як засвідчують аналітичні звіти Українського центру оцінювання якості освіти, результати виконання цих завдань в останні роки суттєво погіршилися, що вимагає пошуку шляхів удосконалення методики вивчення змістової лінії функція у шкільному курсі алгебри та початків аналізу шляхом посилення прикладної спрямованості навчання.

Значну роль прикладних задач у навчанні математики, зокрема в навчанні алгебри та початків аналізу, розкрито в працях Л.О. Соколенко [2],
В.О. Швеця [2], О.В. Сухорукової [3], М.А. Терешина [4] та ін.

У процесі розв’язування прикладних задач здійснюється навчання учнів елементам математичного моделювання, адже найбільш відповідальним і складним етапом розв’язування прикладної задачі є побудова її математичної моделі. Дидактичні цілі, що досягаються в процесі розв’язку прикладних задач під час вивчення похідної та інтегралу у курсі алгебри та початків аналізу – це: 1) підготовка до вивчення учнями похідної та інтегралу, зокрема, шляхом сприяння концентрації уваги учнів на новому понятті; забезпечення мотивації навчання; створення проблемної ситуації; 2) закріплення тільки що набутих теоретичних знань та формування в учнів відповідних математичних компетентностей; 3) аналіз набуття учнями математичних компетентностей зі знаходження похідної та інтегралу та їх застосування.

Окрім того, прикладні задачі повинні давати можливість учням поряд із набуттям математичних компетентностей засвоювати факти суміжних предметів, тобто бути засобом здійснення міжпредметних зв’язків, формування ключових компетентностей.

В залежності від дидактичних цілей, що ставляться вчителем, прикладні задачі можна використовувати на різних етапах уроку, наприклад, при введенні нових понять, а також в самостійній роботі учнів.

Нами створена система прикладних задач, що може бути використана в класах економічного профілю для усвідомлення учнями ролі похідної та інтегралу у економічній науці.

Наприклад, при вивченні застосування похідної до розв’язування задач в класах економічного профілю доцільно запропонувати розв’язати наступну задачу. Прибуток від реалізації товару за ціною p складає: (грошових од.), де . Чи вигідне подальше підвищення ціни?

Розв’язання. Знайдемо похідну і простежимо за поведінкою функції. Похідна цієї функції: додатна, якщо і від’ємна, якщо Це означає, що із зростанням ціни виручка спочатку збільшується (не дивлячись на падіння попиту) і при досягає максимального значення 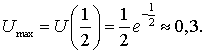Тобто, подальше збільшення ціни не має сенсу, оскільки воно веде до скорочення виручки.

При вивченні застосування інтегралу до розв’язування задач в класах економічного профілю доцільно запропонувати розв’язати наступну задачу. Під будівництво гідроелектростанції заданий безперервний грошовий потік зі швидкістю (млрд грн./рік) протягом років з річною процентною ставкою . Знайти дисконтну вартість цього потоку.

Розв’язання. Учням доцільно нагадати формулу знаходження дисконтної вартості 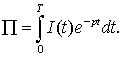Маємо . Щоб обчислити цей інтеграл, виконаємо спочатку заміну змінної: . При цьому нові межі інтегрування отримуємо підстановкою старих меж у формулу заміни: . Маємо 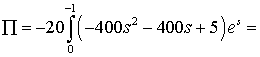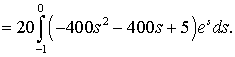До останнього інтеграла застосуємо формулу інтегрування за частинами, приймаючи що Звідси 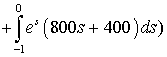. У першому доданку встановимо межі інтегрування, а в другому доданку, застосуємо формулу інтегрування за частинами, приймаючи . Маємо, .

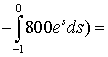
Остаточно одержуємо (млрд. грн.).

Результати навчання за розробленою методикою показали, що викорис-тання прикладних задач на різних етапах уроку сприяє підвищенню мотивації учнів при вивченні похідної та інтегралу, активізації їх роботи у процесі закріплення щойно набутих знань, формування в учнів вміння застосовувати отримані знання в практичній, наближеній до життєвої ситуації, будувати та досліджувати математичні моделі задач, професійній орієнтації учнів.

Література:

1. Арнольд В.И. Математика и математическое образование в современном мире / В.И. Арнольд // Математическое образование. – 1997. – № 2. – С. 7 – 12.

2. Соколенко Л.О. Прикладні задачі природничого характеру в курсі алгебри та початків аналізу: практикум. Навчальний посібник / Л.О. Соколенко,
Л.Г. Філон, В.О. Швець. – К.: НПУ імені М.П. Драгоманова, 2010. – 128 с.

3. Сухорукова Е.В. Прикладные задачи как средство формирования математического мышления учащихся : дис. … кан. пед. наук: 13.00.02 / Сухорукова Елена Владимировна. – МПГУ. – М., 1997. – 192 с.

4. Терешин Н.А. Прикладная направленность школьного курса математики / Н.А. Терешин. – М.: Просвещение, 1990. – 96 с.