О.С. Баруздина, А.А. Настулявичус

Череповецкий Государственный Университет, Россия

Исследование покрытий металла методом компьютерного моделирования

Методы молекулярного моделирования в настоящее время являются общепризнанными инструментами изучения свойств веществ на уровне наноструктур. Для уменьшения коррозии металла используют защитные покрытия, которые позволяют увеличить стойкость и долговечность изделий. Самыми распространенными способами защиты металлов от коррозии являются цинковые и полимерные покрытия. Поэтому представляет актуальный интерес исследование структуры поверхностей тонколистового горячеоцинкованного проката, а также проката с полимерными покрытиями, для выявления и классификации дефектов продукции, причин их появления и разработки методов для их устранения[1,2].

Нашей задачей было создание алгоритма для моделирования процесса нанесения этих двух покрытий на металлический лист. Моделирование в обоих случаях проводилось с помощью метода молекулярной динамики [3], которое заключается в рассмотрении ансамбля частиц, имитирующих атомы или молекулы.

I. Моделирование цинкового покрытия

Существует несколько методов оцинкования, таких как: горячее, электролитическое, термодиффузионное, холодное. Нас интересовал процесс горячего оцинкования. Горячая оцинковка осуществляется в несколько этапов: сначала поверхность стали обезжиривают, протравливают и промывают, затем происходит непосредственное цинкование. Заключительным этапом является охлаждение оцинкованного листа или рулона. Горячее цинкование заключается в погружении стальных структур, после надлежащей предварительной обработки, в ванну с расплавленным цинком при температуре приблизительно 450°С. С физической точки зрения этот процесс определяется процессом диффузии: молекулы цинка проникают в железо, а молекулы железа - в раствор цинка. На прочность сцепления покрытия со стальной основой оказывала влияние толщина диффузионного слоя покрытия, которая зависит от температуры металлической полосы и расплава цинка.

Рассматривался алгоритм, входным параметрами которого являлись как физические константы, так и величины, определяющие точность расчета. На начальном этапе брали две системы взаимодействующих частиц (железо и цинк). Частицы располагались на плоскости, вычислялось расстояние между ними. Начальные скорости теплового движения частиц задавались в соответствии с распределением Максвелла. К скорости теплового движения молекул железа также добавлялась скорость движения металлического листа в цинковой ванне.

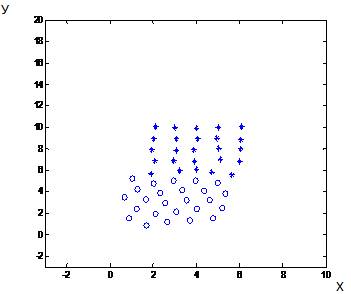
На рис.1. в качестве иллюстрации приведена визуализация компьютерного моделирования процесса цинкования для малого количества частиц.

а) б)

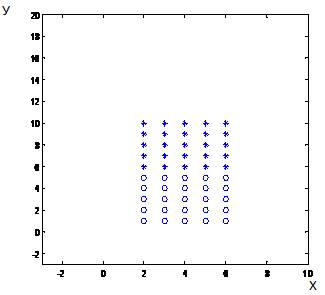
Рис.1.а)Расположение частиц в начальный момент времени б)Положение взаимодействующих частиц через промежуток времени t=0.05.

Целью данной работы являлось определение толщины диффузионного слоя покрытия, которая вычисляется следующим образом:

Так как молекулы железа на рис.1 располагаются сверху, вычисляется величина y₁, которая равна координате y самой нижней молекулы железа. Также вычисляется величина y₂, которая равна координате y самой верхней молекулы цинка. Величина толщины слоя d определялась по формуле :

На рис. 2 представлена зависимость величины толщины от времени, полученные методом молекулярной динамики. Расчеты произведены во внесистемных единицах.

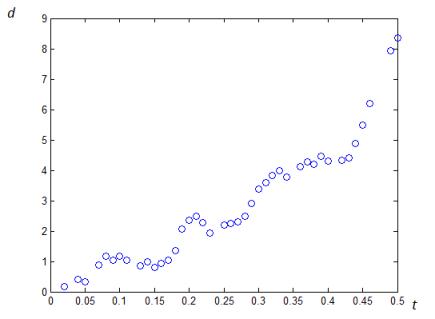
Рис.2. Процесс диффузии (зависимость толщины слоя от времени).

II. Полимерное покрытие

Нанесение полимерных покрытий на оцинкованную сталь - сложнейший процесс, так как стальной лист с полимерным покрытием имеет многослойную структуру: стальной лист, слой цинка, пассивирующий слой, слой грунта, с лицевой стороны - слой цветного полимера, а с  нижней стороны листа «многослойный пирог» завершает защитная краска.

На первом этапе была выполнена программа движения полимерной цепочки, которая рассматривалаль в виде модели Рауза [4]. То есть полимерная цепь представлялась в виде набора частиц (бусинок), соединенных пружинками. Далее программа усложнялась введением растворителя, который испаряется в печи в процессе сушки. Поэтому концентрация растворителя зависит от времени и температурного режима печи. Молекулы растворителя диффундируют изнутри через плотный поверхностный слой, образовавшийся вследствие испарения растворителя с поверхности пленки. Частицы (“бусинки”) сталкиваются с молекулами растворителя и изменяют при этом скорость. Частота столкновений (вероятность столкновения) пропорциональна концентрации, а изменение скорости пропорционально квадратному корню от абсолютной температуры.

Затем рассмотрели процесс прилипания. Если частица в результате теплового движения сталкивается с поверхностью, она может либо зеркально отразиться от нее, либо оказаться крепко связанной с поверхностью, то есть стать адсорбированной. Возможно также обратное явление десорбции, когда адсорбированная частица, имеющая достаточную кинетическую энергию, покинет поверхность. Прилипание возникает только в том случае, если кинетическая энергия частицы будет больше высоты потенциального барьера.

Количество прилипших частиц зависит от времени. Если времени недостаточно, то прилипания не возникнет.

Как видим, полимерные молекулы значительно лучше прилипают к поверхности металла, чем низкомолекулярные вещества.

Имитационное моделирование процессов адгезии полимерных покрытий на поверхности металлического листа является актуальной задачей как для физики конденсированного состояния, так и создания автоматических систем управления в технологических линиях производства.

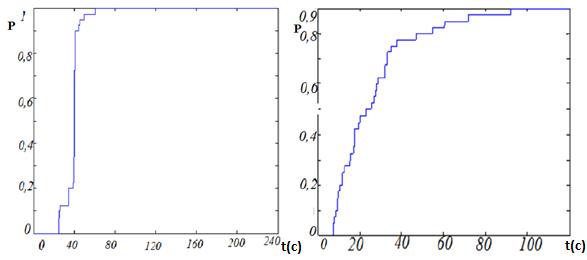
а) б)

Рис.4. Зависимость коэффициента прилипания от времени. а)Высокомолекулярные вещества б)низкомолекулярные вещества.

Заключение:

Результаты предварительного моделирования, подтверждают, что разработанные алгоритм и программа правильно интерпретируют процесс нанесения цинкового и полимерного покрытия на поверхность металлического листа.

Литература:

1.Тихомиров Г.Н., Кельчевский С.М. Справочник по окрашиванию рулонного металла валковым методом. – Москва, 2007

2.Буклет Beckers. Производство окрашенного листа. – Beckers, 2004

3.А.В. Комолкин, М.Г. Шеляпина.Метод молекулярной динамики (учебно – методическое пособие). Санкт-Петербург, 2007 год.

4.А.Ю.Гросберг, А.Р.Хохлов. Статистическая физика макромолекул. М. : Наука, 1989.