Технические науки/4. Транспорт
Моисеев К.
К.
Московский
авиационный институт (Национальный исследовательский университет)
Математические модели двухзвенного гусеничного тягача, движущегося по
грунту с регулярными неровностями
В последнее время перед конструкторами
поставлена задача по увеличению скорости движения «двухзвенника» до 70-80
км/час с целью повышения мобильности агрегатов, а также их боевых и
эксплуатационных качеств. Однако при испытаниях инженеры столкнулись с
необходимостью управления динамическими характеристиками при движении тягача по
волнистому макропрофилю местности. В некотором диапазоне скоростей возникали
околорезонансные и резонансные режимы, которые приводили к существенному усложнению
управления агрегатом и к поломкам поворотно-сцепного устройства. Одним из путей
решения задачи по устранению негативных последствий резонансных режимов
конструкторы видят в возможности изменения параметров демпфирующих свойств поворотно-сцепного устройства. Для того
чтобы решить эту задачу, необходимо разработать расчётную схему и математическую
модель двухзвенного тягача, описывающую его динамическое поведение при движении
по волнистому микропрофилю рельефа местности. Прежде чем перейти к разработке
расчётной схемы рассмотрим физическую модель двухзвенного гусеничного тягача
ДТ-30П, которая представлена на рис. 1 [1]. Согласно физической модели двухзвенного тягача крутящийся момент от двигателя
через гидромеханическую трансмиссию передаётся на оба звена
одновременно, поэтому изменением скорости звеньев в направлении движения можно
пренебречь.
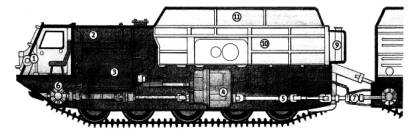
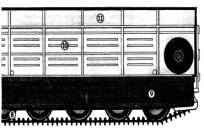
Рис. 1. – Физическая модель двухзвенного плавающего транспортера ДТ «Витязь»:
1 – четырехместная кабина; 2
– моторный отсек; 3
– двигатель; 4 – гидромеханическая
коробка передач; 5 – карданный
вал; 6 – бортовой редуктор; 7 – поворотно-сцепное устройство; 8
– опорный каток; 9
– топливный бак; 10 – грузовая платформа; 11 –
тент.
Последнее обстоятельство важно потому, что
силами реакций упругих связей шарнирного сочленения звеньев можно также
пренебречь. Поворотно-сцепное устройство с четырьмя гидроцилиндрами
обеспечивает в основном демпфирующую связь при колебании центров масс звеньев в
направлении перпендикулярном движению тягача и при угловых перемещениях звеньев
относительно центра шарнирного соединения. Влиянием гусениц на первом этапе исследований
можно пренебречь и считать, что абсолютно твёрдые колёса огибают профиль
местности, не отрываясь от него. Учитывая, что рассматриваются низкочастотные
колебания двухзвенного тягача, возникающие в процессе его прямолинейного
движения по волнообразному рельефу местности, длина волны которого соизмерима с
длиной отдельного звена тягача и то, что мощная рама тягача обладает большой
жёсткостью и, следовательно, довольно значительной величиной собственных частот
колебаний, то в рассматриваемом диапазоне низких частот её динамическое
поведение можно описать как движение абсолютно твёрдого тела. То же самое можно
сказать и о других составных частях звеньев, упругие перемещения которых в
низкочастотной области внешнего воздействия будут неизмеримо малыми по
сравнению с перемещениями всего корпуса гусеничного тягача. Поэтому раму тягача
и все прикреплённые к ней составные части (двигатель, трансмиссию и т. д.) в
целом можно представить в виде абсолютно твёрдого тела, геометрические размеры
и массовые характеристики которого совпадают с физической моделью звена. Каждое
звено соприкасается с грунтом через невесомые упруго-вязкие соединения (связи)
и жёсткие колёса.
Изучение резонансных режимов колебаний
СПУ как динамической системы наиболее целесообразно осуществлять, используя
просто гармоническое возбуждение, например, используя следующее описание
макропрофиля [2] (рис. 3):
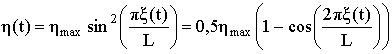 , (1)
, (1)
где ![]() продольная
координата, зависящая от скорости движения транспортного средства
продольная
координата, зависящая от скорости движения транспортного средства ![]() и от времени
и от времени ![]() ;
;![]() длина волны микропрофиля,
длина волны микропрофиля, ![]() максимальное значение
амплитуда волны микропрофиля.
максимальное значение
амплитуда волны микропрофиля.
С учётом вышесказанного при составлении
расчётной схемы принимаем следующие допущения:
1.
Каждая
из гусениц тягача в каждый момент времени проходит микропрофиль с одинаковыми
параметрами.
2.
Тягач
и прицеп представляются в виде абсолютно твёрдых тел, размеры которых совпадают
с соответствующими размерами этих элементов.
3.
Влияние
гусениц на динамику транспортного средства не учитывается.
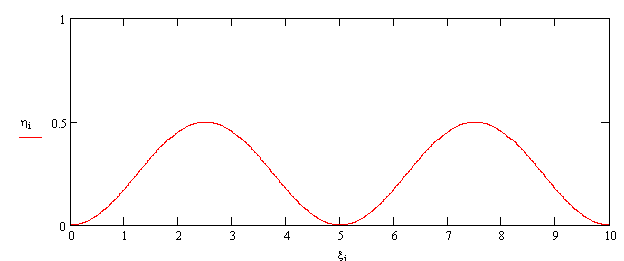
Рис.
3. – Выбранный рельеф микропрофиля для исследования резонансных режимов
«двухзвенника».
4.
Деформацией
грунта и колёс пренебрегаем.
Первое допущение позволяет свести
решение пространственной задачи к её решению на плоскости, когда все точки
исследуемой системы совершают движение в одной плоскости.
Второе допущение определяет частотные
пределы исследований, исключая из них высокочастотные составляющие,
свойственные балочным и оболочечным колебаниям.
Третье допущение позволяет учесть
влияние параметров макропрофиля на каждое колесо тягача и грузового прицепа.
Четвёртое допущение позволяет упростить
математическую модель двухзвенного тягача, исключая из неё описание движения
колёс, так как масса каждого колеса мала по сравнению с суммарной массой рамы,
двигателя, трансмиссии, баков с горючим и кабины. Кроме того, колёса сделаны из
достаточно прочного материала и их деформацией можно пренебречь. Что касается
грунта, то, как уже говорилось ранее, гусеницы сглаживают мелкие неровности и являются
достаточно твёрдой прокладкой между грунтом и колёсами тягача, поэтому
упругость грунтовой поверхности также можно не учитывать. Кроме того, можно
считать, что все упруго-вязкие параметры подвесок колёс имеют одинаковые
величины.
Исходя из принятых допущений,
схематично гусеничный «двухзвенник» можно представить так, как она показано на
рис. 4.
Математическая модель, описывающая
колебательные процессы «двухзвенника», включает в себя уравнения
поступательного движения центров масс твёрдых тел и уравнения,
определяющие вращательное движение тел
относительно центров масс [2,4].
Движение центра масс каждой части
двухзвенного тягача определяется каждой упруго-вязкой связью колёс, на которые
опираются абсолютно упругие тела звеньев, и вязко-упругой связью гидросистемы,
соединяющей между собою звенья тягача.
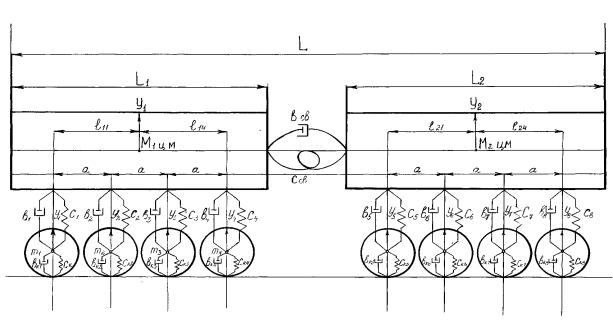
Рис.
4. – Расчётная схема двухзвенного гусеничного тягача
В свою очередь, усилия от упруго-вязких
связей колёс зависят от перемещения центра масс каждого звена ![]()
![]() и от деформации упруго-вязких связей,
определяемых угловыми перемещениями тела относительно центра его масс
и от деформации упруго-вязких связей,
определяемых угловыми перемещениями тела относительно центра его масс ![]() ,
где
,
где![]() порядковый номер колеса. Считая, что перемещения звена
удовлетворяют допущениям, принятым в линейной теории колебаний, можно записать
порядковый номер колеса. Считая, что перемещения звена
удовлетворяют допущениям, принятым в линейной теории колебаний, можно записать 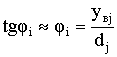 , где
, где ![]() расстояние от
расстояние от![]() го колеса до центра масс
го колеса до центра масс ![]() го звена. Если учесть, что исследуется влияние вязко-упругих
параметров гидросистемы на колебательные процессы «двухзвенника», то в качестве
перемещений, пропорциональных угловым поворотам звена, можно принять
перемещения его конечных точек
го звена. Если учесть, что исследуется влияние вязко-упругих
параметров гидросистемы на колебательные процессы «двухзвенника», то в качестве
перемещений, пропорциональных угловым поворотам звена, можно принять
перемещения его конечных точек ![]() . Тогда каждое перемещение
. Тогда каждое перемещение ![]() можно выразить через
перемещение
можно выразить через
перемещение ![]() :
:
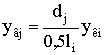 . (2)
. (2)
Уравнения движения центров масс первого
и второго тела с учётом обозначений на рис. 4 и согласно принципу Даламбера
можно записать таким образом [2,4]:
![]()
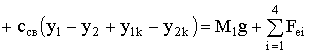 ;
;
![]()
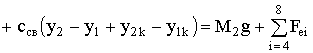 ; (3)
; (3)
Вращательное
движение тел (уравнение моментов) можно описать такими дифференциальными
уравнениями:
![]()
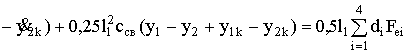 ;
;
![]()
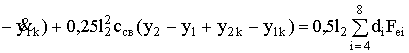
где
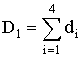 ;
;
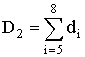 ;
;
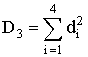 ;
;
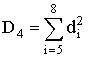 ;
;
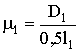 ;
;
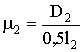 ;
;
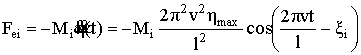 ;
; ![]() фазовый сдвиг, зависящий от расстояния
фазовый сдвиг, зависящий от расстояния ![]() от первого колеса до
от первого колеса до ![]() го;
го; ![]() расстояние от центра масс до
расстояние от центра масс до ![]() го колеса.
го колеса.
Таким образом, уравнения (3, 4)
представляют собой математическую модель динамического поведения двухзвенного
гусеничного тягача, движущегося с постоянной скоростью по волновому рельефу
местности с постоянной длиной волны и определённым значением амплитуды.
В плане
дальнейших научных исследований предусматривается сведение системы из
четырёх линейных дифференциальных уравнений второго порядка к дифференциальному
уравнению восьмого порядка, решение которого может быть осуществлено
численно-аналитическим методом на ЭВМ [3] для различных дорожных воздействий,
соответствующих не только тестовому гармоническому воздействию, но и реальным
условиям эксплуатации. Анализ полученных результатов позволит принять
правильные технические решения по повышению плавности хода двухзвенного тягача,
т. е. по совершенствованию элементов
подвески тягача; конструкции поворотно-сцепного устройства и его
конструктивно-компоновочной схемы.
В
заключении необходимо отметить, что уникальные особенности ТТХ российских
двухзвенных гусеничных тягачей, позволяют сделать вывод о возможности их
широкого применения в качестве универсального транспортного средства в составе перспективных мобильных ракетных комплексов (РК). Тягачи рассматриваемого
класса способны обеспечивать в составе РК: разведку местности и инженерное
обеспечение районов патрулирования; решать задачи охраны и обороны;
транспортировку различных грузов; перевозку личного состава, вооружения и
аварийно-спасательные работы в любых условиях эксплуатации и боевого применения
существующих и перспективных мобильных РК.
Литература
1.
Осколков К.В. Первые отечественные сочленённые гусеничные машины – двухзвенные
транспортёры «Витязь». – Уфа: Издательство «Слово», 2005. – 280 с.
2. Белов
Г.П., Сергеев С.А. Динамика СПУ при транспортировке. г. Серпухов, СВВКУ,1987 г.
с. 152
3.
Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. MATLAB 7. – СПб.: БХВ-Петербург, 2005. – 1104с.: ил.
4. Степанченко Э. П., Фалалеев П. П.
Технологическое оборудование. Основы конструкции и расчёта базовых машин. – М.:
Москва, 1986. – 364 с.