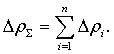Д.т.н. В.В. Мартынов, к.т.н. Е.П. Зинина, В.О. Стариннова

Саратовский государственный технический университет

имени Гагарина Ю.А., Россия

РЕГРЕССИОННЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ ПРОЦЕССА ПЛАЗМЕННОЙ МОДИФИКАЦИИ МЕТАЛЛОРЕЖУЩЕГО

ИНСТРУМЕНТА

Результаты экспериментальных исследований воздействия низкотемпературной плазмы на рабочую часть металлорежущего инструмента, выполненных методом планирования дробного факторного эксперимента [1], позволили установить, что повышение ее микротвердости происходит в различной степени (рис.1) и связано с объективно существующей неоднородностью структуры поверхностного слоя рабочей части. В этой ситуации микротвердость может быть

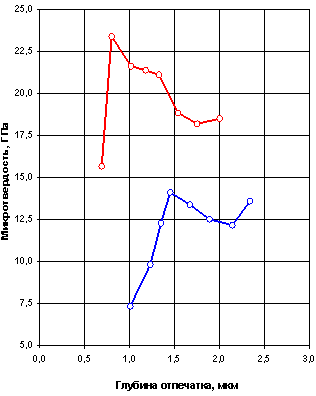
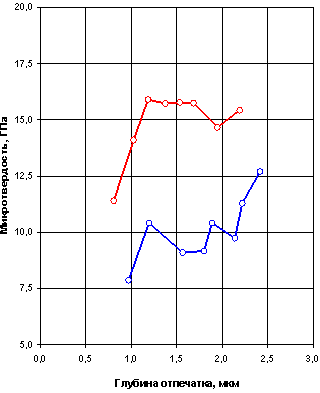
Рис.1. Зависимости микротвердости вершин сменных твердосплавных пластин

от глубины отпечатка до и после плазменной обработки

лишь частным показателем эффективности процесса модификации, поскольку характеризует изменение свойств материала только в определенной области поверхностного слоя. Для того чтобы найти интегральный показатель процесса модификации воспользуемся результатами измерений микротвердости (рис.1) и выполним следующие процедуры:

– определим плотности материала в поверхностном слое рабочей части инструмента до (r_м) и после (r_и) его модификации как отношение микротвердости (HV, г/мм²) к глубине отпечатка (h, мм), полученного в результате действия приложенной к поверхности рабочей части нагрузки грузами различной массы (20…200 г):

(1)

– найдем разности между значениями плотностей, определенных при одинаковы нагрузках, т.е. приращение плотности (Dr_i):

(2)

– вычислим суммарное приращение плотности

(3)

Данный показатель количественно оценивает уменьшение объема материала в поверхностном слое за счет уплотнения его структуры, поэтому в содержательном плане может трактоваться как интегральной показатель эффективности процесса модификации.

Полученный результат позволяет провести анализ влияния параметров процесса плазменной модификации (потенциала смещения – x₁, подводимой СВЧ-мощности – x₂ и координаты положения инструмента в рабочей камере установки – x₃) на приращение плотности (зависимая переменная y). Полагая, что между переменными y и x₁, x₂, x₃ существует линейная зависимость, представим ее уравнение в виде выражения, которое называется регрессионным уравнением и имеет вид [2]:

yi = a1xi1 + a2xi2 + a3xi3 + ei ,

(4)

где a₁, a₂,…, a₃ – оценки неизвестных параметров a₁, a₂, a₃, e_i – случайная переменная, имеющая нулевое математическое ожидание, постоянную дисперсию и характеризующая отклонение переменной y_i от теоретической линии регрессии.

Для определения вектора a оценок параметров a_j, j = 1, 2, …, m используется система нормальных уравнений, которая в матричной форме записывается как

X′Y = X′Xa ,

(5)

откуда

a = (X′X)^-1 X′Y ,

(6)

где (X′X)^-1 – матрица, обратная X′X; Y = (y_i), i = 1, 2, …, n – вектор зависимой переменной Y = (y_i), i = 1, 2, …, n; X = (x_ij) – матрица независимых переменных, размер которой определяется их числом (m), а также числом наблюдений (n); X′ – транспонированная матрица X [2].

Применение системы (6) к результатам модификации вершин двух сменных твердосплавных пластин (рис.1) позволило получить следующие уравнения:

– 1 вершина: Dr = 466,86 + 0,33x₁ – 0,33x₂ – 2,3x₃;

– 2 вершина: Dr = 220,74 + 0,48 x₁ – 0,67x₂ – 1,17x₃,

которые показывают как параметры x₁, x₂, x₃ влияют на приращение плотности и могут быть использованы для оптимизации процесса модификации по критерию получения максимально возможного значения микротвердости.

Литература

1. Бржозовский Б.М. Исходные предпосылки для экспериментального исследования процесса плазменной модификации рабочей части режущего инструмента / Б.М. Бржозовский, В.В. Мартынов, Е.П. Зинина, В.О. Стариннова // Вестник Саратовского государственного технического университета. – 2011. – №3(58). Выпуск 2. – С.20-24.

2. Четыркин Е.М. Статистические методы прогнозирования / Е.М. Четыркин. – М.: Статистика, 1975. – 184 с.