Экология/6. Экологический мониторинг

К.т.н. Щепетова В.А.

Пензенский государственный университет архитектуры и строительства, Россия

Возможности использования математического моделирования в экологическом мониторинге

 

Под экологическим мониторингом, в основном, подразумевается комплексная система наблюдений, оценка и прогноз изменения состояния окружающей среды под воздействием различных факторов.

На современном этапе развития экологического мониторинга в качестве «инструмента» используют, в основном, различные виды нормирования, их анализ и изучение динамики изменения нормативных показателей. Ограниченность концепции нормирования загрязняющих веществ в природных объектов, которая основана на системе предельно допустимых концентраций уже осознана учеными. Система критериев оценки качества окружающей среды на основе ПДК имеет много недостатков, например она не учитывает взаимодействие различных загрязняющих веществ между собой, аккумуляцию в организмах, метеорологические условия и т.д. Несмотря на то, что ускорены темпы нормирования загрязняющих веществ в окружающей среде, на сегодняшний день нормативы все еще не могут в полной мере отвечать требованиям.

Трудности нормирования заключаются в том, что для большинства загрязняющих веществ, ПДК которых установлены, нет надежных аналитических методов контроля; часто нормируются одни формы веществ, а присутствуют другие. Например, токсичность загрязняющих веществ водных объектов зависит от конкретных гидрохимических, гидробиологических ситуаций, на фоне которых она проявляется; процессы трансформации загрязняющих веществ в водных экосистемах включают в себя целый ряд стадий, причем часто промежуточные продукты оказываются более токсичными, чем исходные загрязняющие вещества и т.д.

В результате того, что ежегодно возрастает опасность нежелательных последствий изменения природной среды, методы исследования системы «человек – природная среда» должны совершенствоваться. Для получения более достоверных данных, отражающих состояние природной системы после воздействия различных факторов, по нашему мнению, следует активно применять в экологическом мониторинге метод математического моделирования.

Математическое моделирование предполагает последовательное выполнение следующих этапов: построение математической модели исследуемого процесса, разработка алгоритма вычисления и программы реализации его на компьютере.

В качестве исследуемого объекта мы выбрали Пензенское водохранилище, оценили его значимость, гидрологические и гидрохимические показатели, геологическое строение и свойства грунтов, состояние ихтиофауны. Нами были изучены возможные источники загрязнения поверхностных вод.

В качестве исследуемых веществ были выбраны тяжелые металлы: никель, кадмий, цинк, ртуть, – в связи с тем, что в последние годы наметился рост их концентрации в водной среде. Для постановки задачи были проанализированы возможные пути их попадания в исследуемый водный объект, начальные концентрации тяжелых металлов. В результате проведенных исследований Пензенское водохранилище мы отнесли к плоскому водоему, поэтому рассматривали задачу распространения тяжелых металлов в плоском пространстве, решая двухмерную задачу диффузии.

Мы представили, что попадание тяжелых металлов в водоем происходит на некотором участке границы водоема. Этот случай достаточно распространен, например, при сбросах загрязняющих веществ в обширный, неглубокий водный массив. Размеры той части границы, через которую происходит загрязнение, малы в сравнении с размерами всей границы водоема. Кроме того, мы считали, что распределение тяжелых металлов по глубине водоема происходило равномерно, и основной процесс диффузии происходил по длине и ширине водоема.

Эти предположения дали возможность рассматривать двухмерное уравнение диффузии, заданное в некоторой области Ω, которое имеет вид:

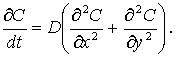                              (5)

Для случая, когда на участке границы от –a до +a находился постоянно действующий источник загрязнения с плотностью p(x, t), а начальная концентрация загрязняющих веществ в пространстве была равна нулю, в качестве граничных условий выбрались следующие:

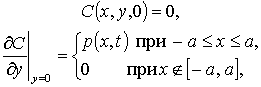                                         (6)

где  – плотность потока примеси; x, y  – соответствующие координаты по длине и ширине водоема.

, , , .

Аналогичную задачу можно рассмотреть для трехмерного характера распространения загрязняющих веществ – сферическую диффузию. Такая экологическая ситуация характерна для случая, когда источник загрязнения находится в неограниченном пространстве, например, на некоторой глубине водоема, а в окружающей среде начальная концентрация равна нулю, то есть  при . Распространение примеси в однородной среде происходит симметрично во всех направлениях: x, y, z. Следовательно, уравнение пространственной диффузии имеет вид

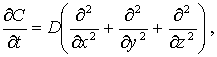                                             (7)

где D – коэффициент диффузии; C – концентрация ЗВ в точке с координатами (x, y, z) в момент времени t.

В сферической системе координат уравнение (7) можно представить в виде:

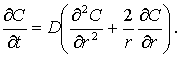                                                (8)

Здесь  – радиус-вектор точки с координатами (x, y, z).

Задачи, учитывающие движение воды, имеют более сложную математическую постановку.

На основании данных математических выражений нами были проведены расчеты, которые позволяют определить концентрацию загрязняющего вещества при попадании некоторого его количества в водоем за определенный промежуток времени.

Расчеты проводились с использованием интегрированной системы MathCAD. Для проверки адекватности математических моделей проводилась численная имитация натурного эксперимента, и полученные расчетные значения концентрации загрязняющих веществ в зависимости от координаты x сопоставлялись с результатами реального натурного эксперимента.

Проведенное сравнение позволило сделать вывод, что полученные в результате численного эксперимента значения хорошо согласуются с опытными данными.

Таким образом, наряду с традиционными методами, применяемыми в экологическом мониторинге при оценке состояния экосистем, возможно использование метода математического моделирования. Данный метод позволяет определять качественный и количественный состав исследуемого объекта при антропогенном воздействии, дает возможность прогноза протекания различных химических и физико-химических процессов, происходящих в экосистеме с учетом различных параметров. Конечно, при составлении подобных моделей следует ограничиваться небольшим количеством факторов, учитывающих распределение загрязняющих веществ, но математическое моделирование способно прогнозировать поведение поллютантов во временном порядке.

Литература:

1. Щепетова В.А., Кузина В.В., Математическое моделирование как метод прогнозирования изменения состояния водных экосистем на примере Пензенского водохранилища // Фундаментальные исследования» № 8 (часть 6) 2013, стр. 1373-1377.

2. Кузина В.В., Кошев А.Н., Математическое моделирование процессов пере­носа примесей в водных экосистемах региона // Математические методы в технике и технологиях: Сб. трудов XXIII Междунар. науч. конф. В 12-и т. Т. 4. Секция 4 / Под общ. ред. В.С. Балакирева. – Саратов: Изд-во Саратовского гос. тех. университета. – 2010. С. 88–91.

3. Кузина В.В., Кошев А.Н., Сухов И.Ф., Математические модели мониторинга техногенных загрязнений водной среды региона // Наука и технологии. Том 2. Труды XXVIII Российской школы. – М.: РАН, 2008. С. 251–258.

4. Роева Н.Н., Баранов А.Н., Щепетова В.А., Гребенкин Н.Н., Моделирование в экологии: Монография. – Рязань: «РИД», 2011. – 188 с.; илл.

5. Щепетова В.А., Толстова Т.В., Анализ экологического состояния Пензенского водохранилища // Фундаментальные исследования. 2011. № 8, часть №1. С. 188 – 189.