Продвинутые
критерии риска «разорения»
Васильев Е.В.
Васильев В.Д.
Тюменский государственный архитектурно-строительный
университет,
г. Тюмень
«Ежегодный доход 20
фунтов, ежегодный расход 20 фунтов, 6 пенсов, и в итоге – нищета. Цветы
увядают, листья опадают, дневное божество озаряет печальную картину»
(Ч.
Диккенс. «Давид Копперфильд»)
Многочисленные прикладные задачи, связанные,
например, с выбором эффективных инвестиционно-инновационных проектов,
формированием оптимальных портфелей финансовых активов, структурированием
кредитных, депозитных и страховых стратегий, оценкой вариантов функционирования
и развития фирм и корпораций, основываются на методологии денежных потоков и
концепциях нормативной (рациональной) теории принятия решений в условиях риска
и неопределенности [1-4].
В самом обобщенном виде любая аналогичная задача
выбора может быть представлена в стандартном матричном формате, для элегантной
формализации которого введем следующее обозначения:
-
Х==
) – варианты решений (проектов, стратегий, действий etc)
представляющих собой компромиссное 
(эффективное) множество по В. Паретто [1,4];
-
– варианты сценариев, ситуаций развития
событий в перспективе (состояний Природы) в смысле различных комбинаций (как
декартово произведение) значений тех изменяющихся рассматриваемых переменных
(факторов), которые являются известными, но не управляемыми и представляющими
собой элементы риска и неопределенности (доходность активов, процентные ставки,
финансовые инструменты, налоги, цены, объем рынка, ставка рефинансирования,
схемы финансирования, валютные курсы, действия регулятора etc);
-
– матрица оценки
абсолютных (или нормализованных) результатов (исходов), получаемых при выборе 
Х и реализации . В общем случае матрицу А можно
рассматривать c двух крайних позиций: 
– матрица выгод (
); 
– матрица потерь (
-
– критерии
оптимальности (решающие правила) выбора наилучших решений в чистых стратегиях;
отражают
разнообразие концептуальных и содержательных критериальных смыслов инвесторов,
игроков, трейдеров, стейкхолдеров, ЛПР.
В итоге, на основе матрицы результатов
(исходов) А мы получаем многокритериальную оптимизационную задачу вида:
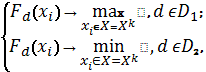
где 
– подмножества
номеров критериев оптимальности, которые соответственно максимизируются и
минимизируются (
).
Не вдаваясь в детальные аналитические
хитросплетения и концептуальную проблематику компромиссной оптимизации [1,2],
здесь отметим только одно важное обстоятельство. Оно заключается в том, что при
формировании схем (сверток) компромиссных критериев нами предполагается
использовать принцип «разумной достаточности», который сводится к тому, что для
Х вводятся два непересекающихся подмножества вариантов сценариев:
«хороших» –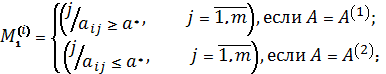 
«плохих» –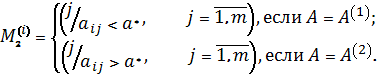 
Здесь значение оценки (а*)
рассматривается как достаточный, желательный, приемлемый, пороговый,
комфортный, разумный результат.
Ситуация принятия решений в условиях
классического риска [2-4] определяется вектором вероятностей потенциальных
возможностей реализации сценариев:
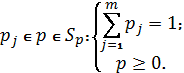
В дополнение к подмножествам 
и 
, формируемых сравнением значений с желаемой (комфортной) оценкой а*, ЛПР также может распределить вектор оценок на подмножества 
, которые отражают желательность, полезность, «удачливость»
конкретных значений . Например, к l=1
относятся неприемлемые (неудачные) оценки-результаты; l=2 – приемлемые; l=3 – нейтральные; l=4 – средние; l=5 – хорошие
(удачливые); l=6 – отличные; l=7 – превосходные. Можно
проще: l=1 – неудачные; l=2 – нейтральные; l=3 – усиленные.
При этом в любом случае совершенно естественным
выглядит обязательное выполнение условия: 
.
Значимость, весомость, доминантность состояний
Природы (сценариев), определяющих получение оценок 
для 
Х, ЛПР непринужденно задает гибкой схемой приоритетов
классического вида:
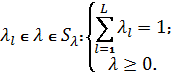
Дефиниция «разорение» применительно к ЛПР нами
рассматривается в самом широком метафизическом, сакральном, семантическом
смысле. Конечно, могут быть использованы и стандартные, образные клише: пустить
по миру, обобрать до нитки, остаться в одной рубашке, ходить с сумой, впасть в
нищету, вылететь в трубу etc.
Более общие, абстрактные символьные ситуации
могут определяться как: финансовые и другие потери; судебные приставы описывают
скудные остатки активов; жалкие, сомнительные результаты и достижения; «потеря
лица» или репутации из-за неудач, провалов, неурядиц; недостижение поставленных
целей, результатов, показателей, характеристик, индикаторов. Именно в этом
последнем понимании «разорения» и были ранее введены два непересекающихся
подмножества: 
Х.
Наиболее распространенные критерии риска
«разорения» можно представить в следующем виде.
Схема 0
Это классические (традиционные) риски, которые
логичны, непротиворечивы, но весьма лапидарны и мало информативны. В связи с
этим приведем ряд других, более элегантных и стильных моделей расчета риска
«разорения», основанных на теории многокритериальной оптимизации [1] и методах
риск-менеджмента [2-4].
Схема 1
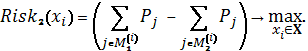
Схема 2
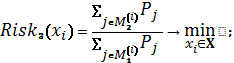
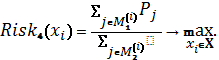
Схема 3
Схема 4
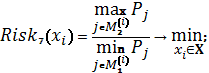
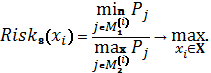
Схема 5
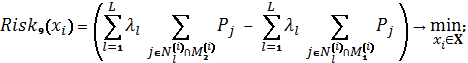
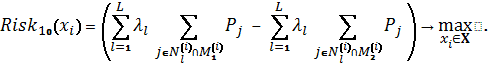
Схема 6
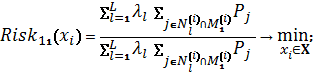
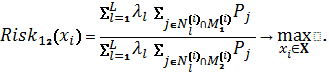
Схема 7
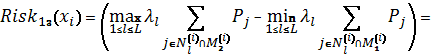
Схема 8
Схема 9
Схема 10
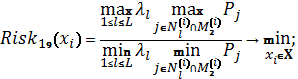
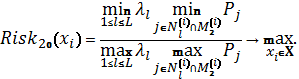
Схема 11
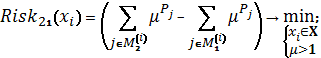
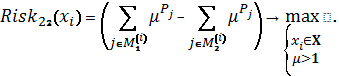
Схема 12
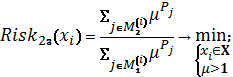
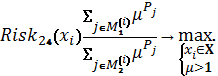
Схема 13
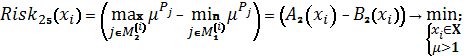
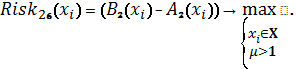
Схема 14
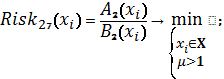
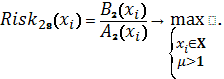
Схема 15
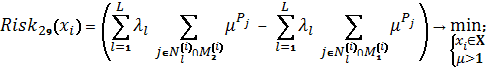
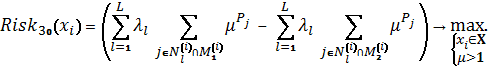
Схема 16
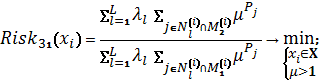
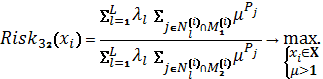
Схема 17
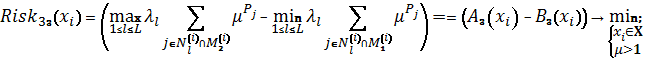
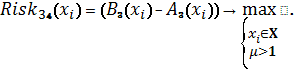
Схема 18
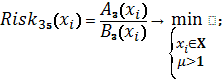
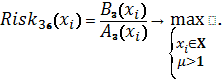
Схема 19
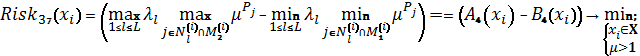
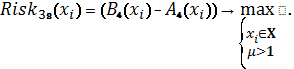
Схема 20
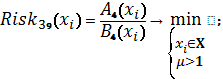
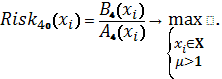
Схема 21
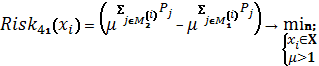
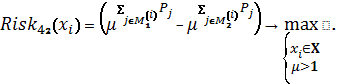
Схема 22
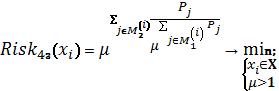
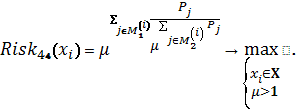
Схема 23
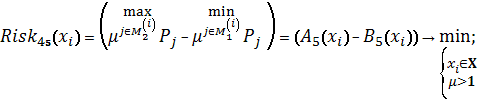
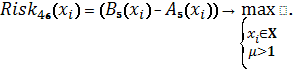
Схема 24
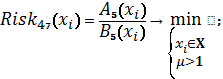
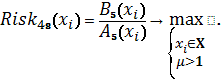
Схема 25
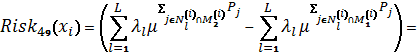
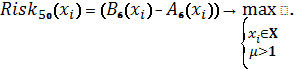
Схема 26
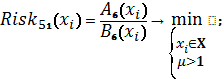
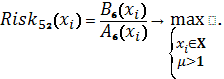
Схема 27
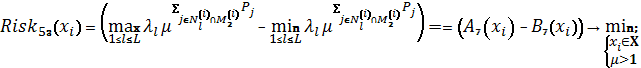
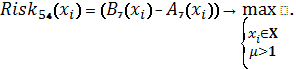
Схема 28
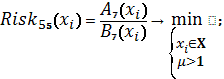
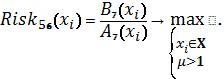
Схема 29
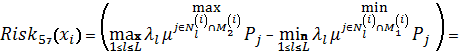
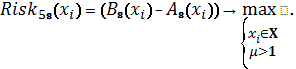
Схема 30
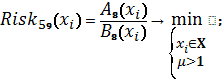
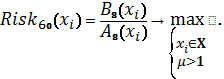
Схема 31
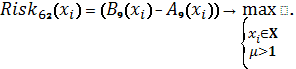
Схема 32
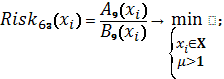
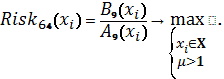
Схема 33
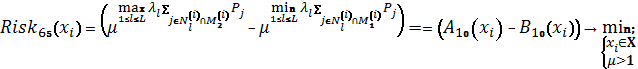
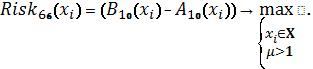
Схема 34
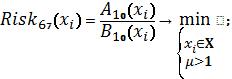
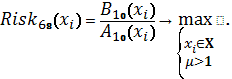
Схема 35
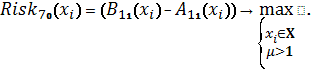
Схема 36
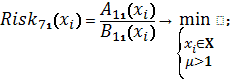
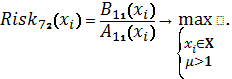
Схема 37
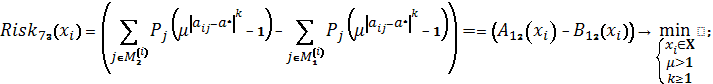
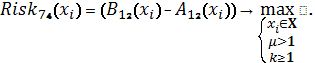
Схема 38
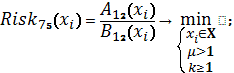
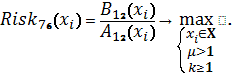
Схема 39
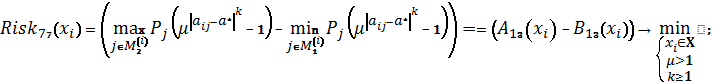
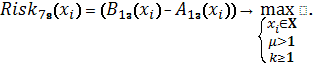
Схема 40
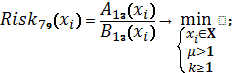
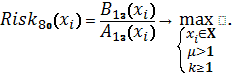
Схема 41
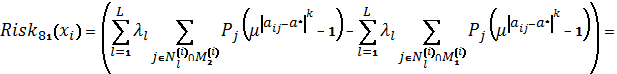
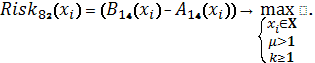
Схема 42
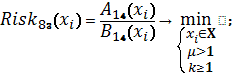
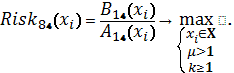
Схема 43
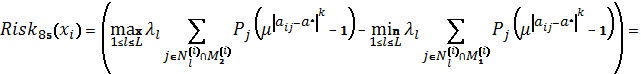
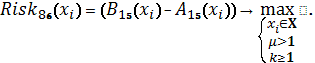
Схема 44
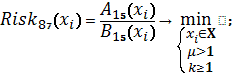
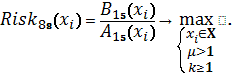
Схема 45
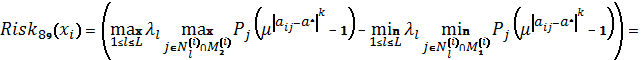
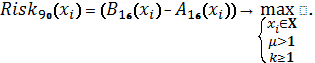
Схема 46
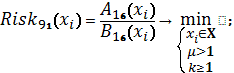
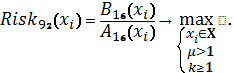
Показанное дефиле этих многообразных и
одновременно своеобразных от изящно-манерных до брутальных критериев выбора
наилучших решений в ситуации риска, конечно, не является полным и
исчерпывающим. Видимо, мир этих удивительных конструктов достаточно велик, что
вселяет некоторые надежды на меланхоличное продолжение начатых исследований и
явление адептам и неофитам других ярких перформансов критериальных оценок.
Настоящим и будущим ЛПР остается или только запастись терпением, или поторопить
авторов существенно ускориться в создании новых весьма любопытных класса luxury
апокрифов.
Список
литературы
1) ВАСИЛЬЕВ В.Д. Оптимизационный подход к выбору
инвестиционных стратегий и проектов в строительстве объектов региона. – СПб.:
Изд-во СПбГУЭФ, 2004. – 287 с.
2) ТРУХАЕВ Р.И. Модели принятия решений в
условиях неопределенности. – М.: Наука, 1981. – 258 с.
3) Малыхин В.И. Математика в экономике. –
М.:ИНФА – М, 1999. – 356 с.
4) Шапкин А.С. Экономические и финансовые риски.
Оценка, управление, портфель инвестиций. – М.: Дашков и Ко, 2006. –
544 с.