Математика/1. Дифференциальные и интегральные уравнения
К.ф.-м.н. Битимхан С.
Карагандинский
экономический университет Казпотребсоюза, Казахстан
Об условиях интегрируемости
тригонометрических рядов с коэффициентами из класса RBSVS
В работе рассматривается класс числовых
последовательностей RBSVS и доказывается аналог
теоремы Харди-Литтльвуда для косинус рядов Фурье функции ![]() , коэффициенты Фурье которые принадлежат к классу RBSVS.
Также получена оценка сверху наилучшего приближения функции
, коэффициенты Фурье которые принадлежат к классу RBSVS.
Также получена оценка сверху наилучшего приближения функции ![]() , при условии, что коэффициенты Фурье
, при условии, что коэффициенты Фурье ![]() .
.
Пусть ![]() неотрицательная,
неотрицательная, ![]() - периодическая функция, заданная на
- периодическая функция, заданная на ![]() . Через
. Через ![]() обозначим
пространство всех измеримых по Лебегу
обозначим
пространство всех измеримых по Лебегу ![]() - периодических функций
- периодических функций ![]() для которых [1]:
для которых [1]:
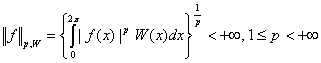 .
.
Будем говорить, что функция ![]() удовлетворяет
удовлетворяет ![]() - условию, если [1]
- условию, если [1]
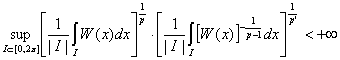 ,
,
где
![]() - длина интервала
- длина интервала ![]() и
и ![]() .
.
Известно, что при ![]() почти всюду на
почти всюду на ![]() пространство
пространство ![]() есть пространство
есть пространство ![]() [1].
[1].
Через ![]() обозначим наилучшее
приближение функции
обозначим наилучшее
приближение функции ![]() тригонометрическими
полиномами порядка не выше
тригонометрическими
полиномами порядка не выше ![]() [2].
[2].
Для двух положительных величин ![]() запись
запись ![]() означает, что
существуют числа
означает, что
существуют числа ![]() такие, что
такие, что ![]() . В дальнейшем через
. В дальнейшем через ![]() будем обозначать
положительные постоянные, вообще говоря, различные в разных формулах.
будем обозначать
положительные постоянные, вообще говоря, различные в разных формулах.
В работе [3] B.Szal
определил
класс числовых последовательностей RBSVS (rest
bounded second variation sequence).
Определение. Нулевая
последовательность неотрицательных чисел ![]() , если
, если ![]() :
:
![]()
для
любых натуральных ![]() .
.
В работе [3] показано, что класс RBSVS
шире чем класс монотонных последовательностей. Поэтому актуальность вопроса
рассмотренного в этой статье не вызывает сомнения.
Теперь приводим доказанные нами утверждения.
Теорема 1. Пусть функция ![]() имеет ряд Фурье
имеет ряд Фурье
![]() ,
,
где
![]() . Если функция
. Если функция ![]() и удовлетворяет
дополнительно условию
и удовлетворяет
дополнительно условию ![]() , то
, то ![]() тогда и только тогда,
когда
тогда и только тогда,
когда
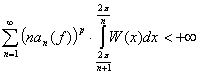 .
.
При этом имеет место соотношения:
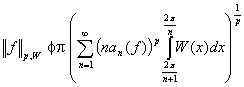 .
.
Замечание. При ![]() из этой теоремы
следует лемма 6 работы [3].
из этой теоремы
следует лемма 6 работы [3].
Теорема 2. Пусть функция ![]() имеет ряд Фурье
имеет ряд Фурье
![]() ,
,
где
![]() . Если функция
. Если функция ![]() , удовлетворяет дополнительно условию
, удовлетворяет дополнительно условию ![]() и
и
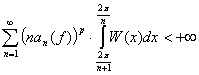
тогда
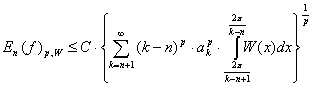 .
.
Доказательство. Пусть ![]() частичная сумма ряда
Фурье функции
частичная сумма ряда
Фурье функции ![]() . Рассмотрим разность
. Рассмотрим разность ![]() . Получим
. Получим
![]() . (1)
. (1)
Известно, что [2]
![]() . (2)
. (2)
С помощью теоремы об ограниченности оператора
сопряжения [2] в пространстве ![]() , из (1) и (2) получим:
, из (1) и (2) получим:
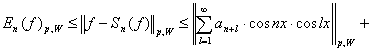
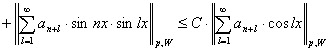 .
.
В работе [4] доказано, что если ![]() , то при фиксированном натуральном
, то при фиксированном натуральном ![]() последовательность
последовательность ![]() . Поэтому пользуясь теоремой 1, из последнего неравенства
получим:
. Поэтому пользуясь теоремой 1, из последнего неравенства
получим:
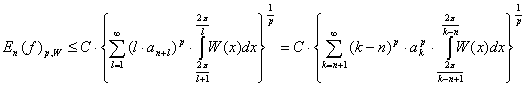 .
.
Теорема 2 доказана.
Литература:
1. Muckenhoupt B.
Weighted norm inequalities for the Hardy maximal function // Trans. American
Math. Soc., 1972, v. 162, P. 207-226.
2. Hunt R., Muckenhoupt
B., Wheeden R. Weighted norm inequalities for the conjugate function and
Hilbert transform // Trans. American Math. Soc., 1973, v. 176, P. 227-251.
3. Szal B. Generalization
of a theorem on Besov-Nikol’skii classes // Acta Math. Hungar., 125(1-2), 2009,
P. 161-181.
4. Асетов А.А., Акишев Г.А. Наилучшее
приближение функции и класс RBSVS // Вестник
Карагандинского университета, серия: математика, 2013(2), С. 22-27.