Математические науки/ 1. Дифференциальные и интегральные уравнения

Д.ф.-м.н. Т.Т. Каракеев, Д.К. Рустамова, Ж.Т. Бугубаева

Кыргызский национальный университет имени Ж. Баласагына, Кыргызстан

Приближенные методы решения линейных интегральных уравнений Вольтерра третьего рода

Вопросы регуляризируемости линейных интегральных уравнений Вольтерра третьего рода рассмотрены в исследованиях [1, 3]. В работе [1] коэффициентная функция вне интеграла является непрерывной и невозрастающей, и обращается в нуль в конце отрезка интегрирования, в работе [3] рассматривается случай неубывающей функции, вырождающейся в начале отрезка интегрирования. При этом методы регуляризации сохраняют свойства вольтерровости уравнения.

В данной работе для линейного интегрального уравнения Вольтерра третьего рода, на основе эквивалентных преобразований и метода регуляризации доказаны единственность и устойчивость решения уравнения, построено численное решение и показана сходимость решения дискретизированной системы уравнений к решению исходного уравнения.

Пусть заданные функции , , входящие в линейное интегральное уравнение Вольтерра третьего рода

решение, которого принадлежит пространству подчиняются условиям:

)

) , ,

) ,

Рассматриваются два случая:

1) Пусть и невозрастающая функция. Действуя оператором , где - единичный оператор, и T– операторы Вольтерра вида

из (1) получим уравнение, эквивалентное к уравнению (1) в смысле разрешимости

Вводится регуляризирующая система уравнений с малым параметром из интервала (0,1)

Посредством резольвенты ядра уравнение (3) преобразуем к следующему виду

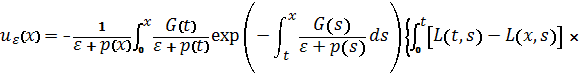
Пусть

где

;

Доказана следующая

Теорема. Пусть выполняются условия а) – в), и уравнение (1) имеет решение Тогда решение уравнения (3) равномерно сходится к решению уравнения (1). При этом справедлива оценка

где

Следствие. При выполнении условий теоремы решение уравнения (1) единственно в .

2) Пусть теперь и неубывающая функция. Пусть также при условие а) сохраняет силу.

Тогда при из (2) и (3) получим уравнения

где

Теорема. Пусть выполняются условия а) - в) и уравнение (1) имеет решение Тогда, при , решение уравнения (5) равномерно сходится к решению уравнения (1) и имеет место оценка

где

Следствие. При выполнении условия теоремы решение уравнения (1) единственно в пространстве

Введем на отрезке равномерную сетку

, n- натуральное число.

Пусть - пространство сеточных функций с нормой

С помощью квадратурной формулы правых прямоугольников из уравнения (5) приходим к следующей системе линейных алгебраических уравнений

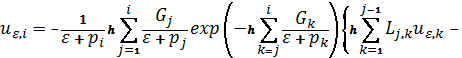
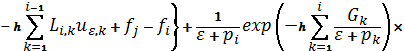
Здесь

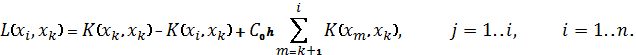
Величину выбираем в виде для которой из условий а) - в) следуют оценки

Теорема. При выполнении условий а) – в) и для всех 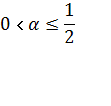, решение системы уравнений (6) при равномерно сходится к - точному решению уравнения, причем имеет место оценка

Литература:

1. Каракеев Т.Т. Регуляризация нелокальной граничной задачи для псевдопараболических уравнений. // Исслед. по интегро-дифференц. уравнениям. - Бишкек: Илим, 2003 –Вып. 32. -С. 179-183.

2. Каракеев Т.Т., Бугубаева Ж.Т. Регуляризация линейных интегральных уравнений Вольтерра III рода // Вестник КНУ им. Ж. Баласагына. - Бишкек 2012. – Вып. 5. - С. 29-33.

3. Каракеев Т. Т., Рустамова Д. К. Регуляризация и метод квадратур для линейных интегральных уравнений Вольтерра третьего рода // Исслед. по интегро-дифференц. уравнениям. – Бишкек 2009. – Вып.40. - С. 127-132.