Математика/5. Математическое моделирование

Baimankulov A.

Kostanay State University named after A.Baitursynov, Kazakhstan.

Apriori estimates of the differential conjugate task

The differential conjugate task, that given in [4] is offered,

, (1)

, (2)

. (3)

Estimates solutions are required to prove the mathematical properties of the problem.

Multiply the system (1) on and sum over all internal nodes of the grid

,

then

.

Apply the formula for summation by parts in the variable

and using the initial-boundary conditions (2)-(3) we have the inequality

.

Using the Cauchy's inequality and assuming, that and using a lemma 5 of [4], deduce that

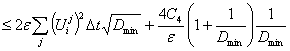. (4)

Taking into account identity

and the assumption that , we obtain

.

Substitute in (4), then at the inequality takes place

.

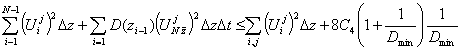Applying the difference analogue of the Gronwall lemma, deduce that

.

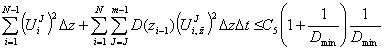References

1.Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1996, 724 с.

2.Рысбайулы Б. Идентификация коэффициента теплопроводности распространения тепла в неоднородной среде // Вестник КБТУ, 2008, №1, ст. 62-65

3.Байманкулов А.Т. Определение коэффициента диффузии почвенной воды в однородной среде.// Известия НАН РК, 2008, № 3, с.45-47.

4.Байманкулов, А.Т. Априорные оценки разностной задачи // Материали за 9-а международна научна практична конференция, «Новината за напреднали наука», - 2013. Том 53. Математика. София. «Бял ГРАД-БГ» ООД. - С. 85-87