Математика/5. Математическое моделирование

Baimankulov A.

Kostanay State University named after A.Baitursynov, Kazakhstan.

Settlement formula for the interfaced task

The differential interfaced task is considered, given in [3]

, (1)

, (2)

. (3)

Let’s show, that the coefficient of capillary diffusion is defined from a functionality minimum

.

Enter designations

_,

_{let’s make a difference of functionalities}

=

Use (1) and parity and copy a difference of functionalities in a look

.

If

then

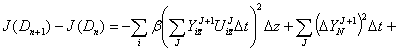
. (4)

We know, that that’s why the recurrence relation turns out

. (5)

For the proof of limitation and monotony of sizes и we need aprioristic estimates of the solution of a straight line and interfaced tasks.

References

1.Юзефович Г.И., Янгарбер В.А. Исследование нелинейного уравнения влагопереноса. // Л.: Колос. Сб. трудов по агрофизике, вып. № 14, 1967.

2.Байманкулов А.Т. Определение коэффициента капиллярной диффузии.// Материали за VIII международна научна практична конференция «Бъдещето въпроси от света на науката -2012», т.36, 17-25 декември, 2012, София.

3.Байманкулов, А.Т. Конечно-разностная аппроксимация прямой и сопряженной задач [Текст] / Байманкулов А.Т., Махамбетова Г.И. // Materialy IX miedzynarodowej naukowi-praktycznej konferencji «Europejska nauka XXI powieka-2013» Volume 27. Matematyka. Fizyka. Budownictwo i architektura.: Przemysl. Nauka i studia - C.22-23.