МАТЕМАТИКА /4.Прикладная математика.

Д.т.н. Коханенко В.Н., к.т.н Лемешко М.А., Цоколова В.В., Глазунова К.В

Донской государственный аграрный университет, Россия

Решение задачи движения охлажденного воздуха при открывании дверей торгового холодильника.

Объектом исследований является процесс движения потока охлажденного воздуха, истекающий из камеры холодильника после открывания его двери. Реальный поток воздуха, истекающий из холодильной камеры, является трехмерным, то есть он характеризуется в каждой точке потока значениями продольной, поперечной и вертикальной проекциями вектора скорости, значениями давления, температуры, вязкости, удельной теплоемкости, теплопроводности. Каждый из вышеперечисленных параметров газа является в общем случае функцией четырех переменных: т.е. каждый параметр зависит от трех пространственных координат и времени.

В работах, которые посвящены изучению динамики газовых потоков, уравнения движения потока воздуха выводятся из уравнений Навье – Стокса, дополненных слагаемыми, учитывающими силы сопротивления потоку. При этом следует отметить, что силы сопротивления могут быть вызваны как вязкостью внешней среды, в которой движется поток (вязкость первого рода), так объемной вязкостью, т.е. силами трения элементарных струй потока между собой (вязкость второго рода).

Система динамических уравнений для трехмерных неустановившихся потоков с учетом динамической вязкости первого рода в прямоугольных декартовых координатах в векторной форме имеет следующий вид [1]:

, (1)

где: вектор скорости потока в каждой точке пространства;

плотность газового потока; давление, действующее на газ в каждой точке; вектор внешних объемных сил, действующих на газ в каждой точке пространства; коэффициент динамической вязкости;

тензор скоростей деформаций; дивергенция вектора скорости; проекции вектора скорости на координатные оси ОХ, ОУ, ОZ.

Уравнение неразрывности потока в векторной форме имеет вид:

(2)

В совокупности система трех уравнений движения и неразрывности потока образуют систему четырех уравнений относительно девяти неизвестных функций: проекции вектора скорости;

функции плотности, давления и температуры;

удельная теплоемкость, коэффициент динамической вязкости и коэффициент теплопроводности.

Переходя к плоскости двух координат и делая допущения по ряду параметров можно решить полученные уравнения и получить модель истечения охлажденного воздуха из камер холодильника при открывании дверей камеры

При сформулированных выше допущениях система уравнений, описывающая истечение воздуха из холодильной камеры, содержит семь неизвестных функций: . В таком случае для замыкания системы дифференциальных уравнений в частных производных необходимо иметь семь уравнений.

В вышеописанной постановке задачи таких уравнений предложено шесть, в качестве седьмого уравнения для замыкания системы может быть предложено уравнение диффузии, либо уравнение теплового баланса. При этом делаем допущения, определяющие граничные условия задачи:

1). Равенство нулю скорости на неподвижной твердой границе между внутренней поверхностью корпуса шкафа и движущимся воздухом.

2). Начальные скорости истечения холодного воздуха из шкафа равны нулю в каждой точке прямоугольного сечения на выходе из шкафа.

После ряда допущений исходную систему преобразуем к более простому виду:

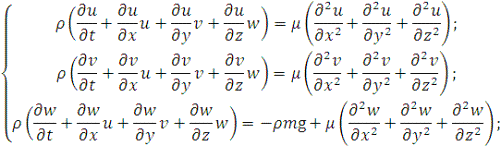(3)

Система (3) является системой трех нелинейных уравнений в частных производных относительно трех неизвестных функций, то есть система (3) является замкнутой.

Систему (3) можно еще более упростить, полагая, что ординаты траекторий движения воздушных струй исследуемого потока постоянны и изменение геометрии потока происходит только в плоскости XOZ (рис.1)

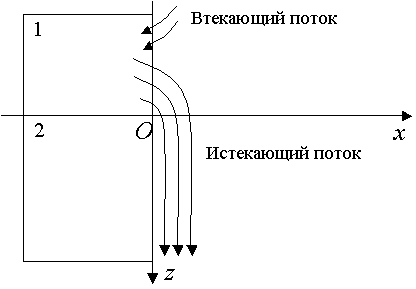
Рис. 1 – схема свободно истекающего потока воздуха

в плоскости XOZ. 1 – холодильная камера; 2 – морозильная камера.

Литература

1. Лойцянский Л.Г. Механика жидкости и газа / Л.Г. Лойцянский. – 5-е изд. – М.: Наука, 1978. – 736 с.

2 Лемешко М.А., Лалетин В.И., Мицик М.Ф./ Определение скоростей движения охлажденного воздуха при открывании дверей шкафа бытового холодильного прибора. Инженерный вестник Дона, 2011. №4. http://www.ivdon.ru/magazine/archive/n4y2011/604/ (доступ свободный).