Маtematika/4. Matematik modeli.

Ryschanova S.M.

Kostanai State University. A.Baitursynov, Kazakhstan

MULTI-CRITERIA OPTIMIZATION

In order to obtain a detailed profile of the advantages and disadvantages of a subject (whether a research subject or any other subject) one should input more criteria of its analysis. As a result, project tasks of the complex systems are always multi-criteria tasks, because one should consider various requirements to the system in order to select an optimal variant. From the standard standpoint a multi-criteria problem has no solutions. Fortunately, it is not so and we always have an opportunity to meet all the required conditions simultaneously. Effective solution of any of the given problems primarily requires the construction of multi-criteria mathematical model that will be optimized, using the most suitable method.

Optimization is used in mathematics and many other spheres. It is an integral part of applied mathematics along with the numerical methods, mathematical physics, liner programming and the other branches of the science.

The problem of multi-criteria mathematical programming can be expressed as follows:

max{f₁(x)=F₁},
max{f₂(x)=F₂},
...
max{f_k(x)=F_k}, whereas xєX,

where X – set of admissible values of the variables х;
k–number of objective functions (criteria);
F_i – value of i criterion (objective function),
“max” means that the given criterion should be maximized.
It should be noted that in fact a multi-criteria problem differs from a standard optimization problem in the presence of several objective functions instead of one function. The first natural step of the solution selection problems formalized as the model of vector optimization should be selection of the region of compromise (or Pareto optimal solutions).
A vector can be considered Pareto optimal solution, if there is no хєХ that will make the following in equations true:
and
Several Methods of Multi-criteria Optimization.

Principle of true compromise. Let’s assume that all the local criteria forming the efficiency vector are of similar significance.

A compromise whereby the relative level of the loss of quality of one or several criteria does not exceed the relative level of the improvement of quality of the remaining criteria (less than or equal to) should be considered true.

Principle of weak Pareto optimality. Vector х1єХ should be considered weak Pareto optimal solution (Slater optimal), if there is no vector х1єХ, that will make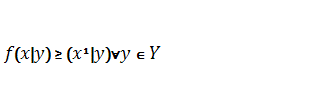
Method of quasi-optimization of local criteria (method of successive eliminations).

In this case one searches not for a single exact optimum, but for a certain region of solutions that are close to the optimal solution, i.e. quasi-optimal set of solutions. Herewith the level of acceptable deviation from the exact optimum can be determined with the accuracy of problem statement taken into account (for example, subject to the accuracy of the criterion value calculation), as well as some practical considerations (for example, requirements to the accuracy of problem solution).

Summary of the Results of Scientific Research and Analysis. Current Issues of Multi-criteria Optimization. In the course of research we have collected the material about the existing methods of multi-criteria optimization and classified it into corresponding sections. Nowadays one can distinguish the following issues of multi-criteria optimization.The first issue is related to the selection of optimality principle that allows accurate determination of the optimal solution property and lets us know the way this optimal solution excels all the other permissible solutions. Unlike the problems of single criterion optimization having only one optimality principle f(xо)>=f(x), this case involves the set of various principles. And application of every single principle can lead to the selection of different optimal solutions. It can be explained by the fact that one has to compare the efficiency vectors on the basis of a certain compromise scheme. In the terms of mathematics this issue is equivalent to the problem of the vector set raking, while the selection of optimality principle is equivalent to the selection of ordering relation. The second issue is associated with the normalization of vector efficiency criterion F. It is caused by the fact that the local criteria that are the components of efficiency vector often have various measurement scales, which makes their comparison difficult. That is why one has to transform the criteria so that they have common measurement scale, i.e .to normalize them. The third issue refers to the consideration of priority (or various significance) of the local criteria. Although selection of the solution requires observation of the maximum quality of each criterion, their degrees of sophistication, however, generally have different significance. That is why consideration of the priority usually involves introduction of the vector of criterion significance distribution L= (l₁, l₂, ..., l_n) with the aid of which the optimality principle is adjusted or criterion measurement scales are differentiated. Possible Solutions of the Issues of Multi-criteria Optimization

The issues analyzed above are associated with the main difficulties of multi-criteria optimization. And their successful overcome predetermines success and accuracy of the solution selection. That is why the person or authority responsible for the selection should necessarily take part in the solution of the given issues. Thus, it is necessary to develop such interactive optimization procedures that require the entry of the essential information by the decision makers in the process of problem solution. This includes information about the relative significance of the criteria, as well as information about the variation of the value of the certain criterion after the last executed step of optimization algorithm. Possible solutions of the multi-criteria optimization issues analyzed above include application of the convolutions and normalizations methods. Another variant of solution of multi-criteria optimization problem is the application of the evolutionary (genetic) algorithms.