Математика/4. Прикладная математика

Моисеева Н.Н.

Государственное бюджетное образовательное учреждение средняя общеобразовательная школа № 1432

Минимизация логических функций двух переменных

Логическая функция — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

  Логический элемент — это устройство, реализующее ту или иную логическую функцию. Y=f(X1,X2,X3,...,Xn) — логическая функция, она может быть задана таблицей, которая называется таблицей истинности.

Теорема 1

Любая функция двух переменных может быть представлена в виде комбинации функций И, ИЛИ, НЕ.

Доказательство

Таблица истинности любой функции имеет вид:

Где Y0, Y1, Y2, Y3 принимают значения 0 или 1. Составим конъюнкцию (ИЛИ) из всех строк, где Yi равно 1. Каждый элемент конъюнкции это дизъюнкция (И) переменных, если Xi = 1 в соответствующей строке или их отрицание, если Xi = 0 в соответствующей строке. Очевидно, что данный элемент конъюнкции равен 1 только для этой строки и 0 для всех остальных.

Тогда, конъюнкция будет равна 1 только для Yi = 1 и 0 во всех остальных случаях. То есть данная конъюнкция будет равна исходной функции. Таким образом, исходная функция представляется через И, ИЛИ, НЕ, что и требовалось доказать.

Пример

Представим через И, ИЛИ, НЕ функцию эквивалентности. Таблица истинности функции имеет вид

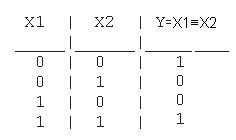
Y = ØX1ØX2 Ú X1X2

Через функции И, ИЛИ, НЕ логические функции могут быть представлены несколькими способами. Поэтому целесообразно минимизировать представление функций с использованием наименьшего количества базовых функций. Для этого служат карты Карно.

Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2N наборах входных переменных X1 ... XN. Карта Карно также содержит 2N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1 ... XN. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.

Минимизация логических функций двух переменных

1. Конъюнкция

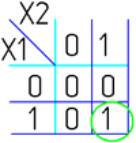X1 X2

2. Запрет по Х1

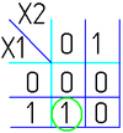ØX1 X2

3. Повторение 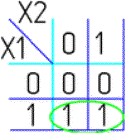X1

X1

4. Запрет по Х2

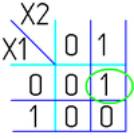X1 ØX2

5. Повторение X2

X2

6. Сложение по модулю 2

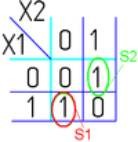ØX1X2 или ØX2 X1

7. Дизъюнкция

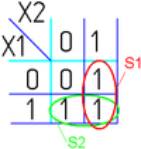X1 или X2

8. Стрелка Пирса

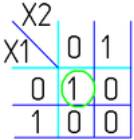
ØX1ØX2

Представление логических функций через базовые функции

Функции И, ИЛИ, НЕ не являются единственным набором базовых функции. Существую ещё несколько наборов базовых функций, представляющих все другие функции.

Проверить является ли набор функций базовым можно на основе следующей теоремы.

Теорема 2

Для того, чтобы набор функций был базовым, то есть представлял все другие функции, достаточно чтобы через этот набор можно было представить функции И, ИЛИ, НЕ.

Доказательство

Любая функция представима через И, ИЛИ, НЕ. Заменим в этом представлении данные функции их эквивалентом через другой базовый набор. Тогда исходная функция представляется через данный базовый набор, что и требовалось доказать.

Представление логических функций через штрих Шеффера

Теорема 3

Через функцию штрих Шеффера Y = X1|X2 = Ø (X1ÙX2) можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция штрих Шеффера была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание ØХ1 =Ø(Х1Ù1) = Х1|1

Конъюнкция Х1Ù Х2 = Ø(Ø(Х1Ù Х2)) = Ø(X1|X2) = (X1|X2) |1

Дизъюнкция Х1ÚХ2 = Ø(ØХ1ÙØХ2) = ØХ1|ØХ2 = (Х1|1)|(Х2|1)

Теорема доказана.

Представление логических функций через стрелку Пирса

Теорема 4

Через функцию стрелка Пирса Y = X1X2 = Ø (X1ÚX2) можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция стрелка Пирса была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание ØХ1 =Ø(Х1Ú0) = Х10

Конъюнкция Х1Ù Х2 = Ø(ØХ1Ú ØХ2) = (ØX1ØX2)=(X10)(X20)

Дизъюнкция Х1ÚХ2 = Ø(Ø(Х1ÚХ2)) = Ø(Х1Х2) = (Х1Х2)0

Теорема доказана.

Представление логических функций через импликацию

Теорема 5

Через функцию импликация Y = X1®X2 = Ø X1ÚX2 можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция импликации была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание ØХ1 =ØХ1Ú1 = Х1®1

Конъюнкция Х1Ù Х2 = Ø(ØХ1Ú ØХ2) = Ø (X1®ØX2)=(X1®ØX2) ®1

=( X1®(X2®1) ®1

Дизъюнкция Х1ÚХ2 = Ø(ØХ1)ÚХ2 = (ØХ1) ®Х2 = (Х1®1)®Х2

Теорема доказана.

Литература:

1. А.А. Ивин Логика, учебное пособие издание 2 Москва, Знание 1998

2. Д.А. Владимиров Булевы алгебры Москва, Наука 1969

3. Википедия свободная энциклопедия, Логика http://ru.wikipedia.org/

4. Н.Н. Моисеева Методические разработки, учебный сайт http://www.schools.keldysh.ru/sch1019/