Физика/10. Физика полимеров

Настулявичус А.А, Максимова О.Г, Байджанов А.Р, Баруздина О.С, Проуторов Е. В.

Череповецкий государственный университет

Моделирование процесса растекания адгезива на поверхности металлического листа

Благодаря своим уникальным свойствам, полимерные материалы нашли широкое применение в различных отраслях промышленности, в том числе и металлургической. Особое внимание уделяется методам защиты от коррозии. Одним из таких является нанесение полимерного покрытия на поверхность металлического листа. Стойкость покрытия определяется физико-химическими свойствами, которые удобно исследовать методами компьютерного моделирования. Также компьютерные методы позволяют оценить необходимые температурные режимы и другие характеристики реального производственного процесса.

Одним из этапов процесса прилипания полимерного покрытия к поверхности металлического листа является растекание лакокрасочного материала (ЛКМ) по поверхности твердого тела и его смачивание [1].

Цель данной работы заключается в создании компьютерной 3d-модели процессов движения и прилипания молекулы к листу металлопроката. Было рассмотрено движение системы мономеров и полимерной цепочки внутри растворителя. Исследование движения полимерной цепи в данной работе проводилось методом молекулярной динамики. В качестве математической модели полимерной цепи была выбрана модель Каргина – Слонимского, в которой макромолекула рассматривается в виде набора «бусинок», соединенных упругими пружинками с жесткостью k (рис.1). Также, при моделировании учтена жесткость цепи на изгиб (константа k₁)

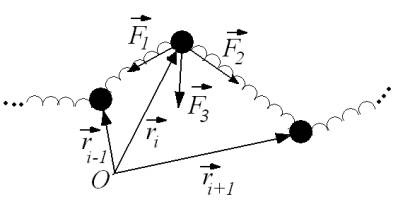
Рис. 1 Модель полимерной цепи

В модели Каргина- Слонимского на выделенную бусинку действуют силы:

, ,

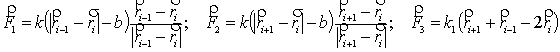, где

- сила, действующая со стороны левой пружинки,

- сила, действующая со стороны правой пружинки,

- сила, с которой связана жесткость цепи на изгиб.

Действие сил на первую и последнюю бусинки определяются граничными условиями. Например, при свободных граничных условиях на первую бусинку действует только сила , а на последнюю - .

Начальные скорости теплового движения частиц подчиняются распределению Максвелла и определяются мгновенной температурой, при которой происходит сушка покрытия.

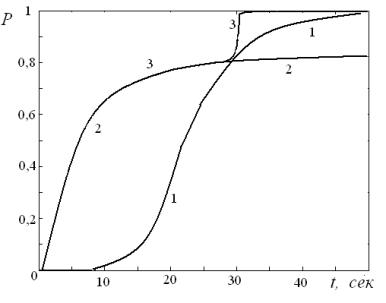
На рис. 2. приведены результаты вычислительного эксперимента по изучению движения полимерной цепи в растворе в направлении к поверхности стали. Показана временная зависимость доли мономеров, достигших поверхности (величина P). Вычисления произведены для полимерной цепочки (кривая 1) и мономеров, не связанных в цепь (кривая 2), а также для случая, когда первоначально ЛКМ был в виде низкомолекулярного вещества, затем произведена полимеризация (кривая 3). Приведенные кривые являются средними.

Рис. 2 Зависимость доли мономеров, достигших поверхности: 1 – полимерная цепочка, 2 – отдельные мономеры, 3 – первоначально отдельные мономеры, через 30 с произведена полимеризация

Как видно из рис. 2, первоначально молекулы раствора, состоящего из отдельных мономеров, быстрее достигают поверхности, так как они имеют большую подвижность по сравнению с полимерными цепями. Однако цепи при своем движении обладают свойством кооперативности, поэтому через некоторое время величина P для цепей становится больше, чем для отдельных мономеров. На рис. 2 показано, что оптимальным для достижений лакокрасочного материала к поверхности металла является следующий режим: первоначально ЛКМ является низкомолекулярным веществом, одновременно в процессе сушки происходит миграция мономеров и их полимеризация. Кроме того, необходимо выбрать такой тепловой режим, при котором требуется меньше количества газа, а растекание максимально

(величина P=1).

Литература

1. Липатов, Ю. С. Коллоидная химия полимеров / Ю. С. Липатов.- Киев: Наук. думка, 1984.- 344 с.