Проуторов Е.В., Байджанов А.Р., Баруздина О.С., Настулявичус А.А.

Череповецкий государственный университет, Россия

Моделирование движения заряженных частиц в молекулярных системах с ориентационными степенями свободы.

Сегнетоэлектрики, жидкие кристаллы, полимерные вещества становятся все более важными для применения в современной промышленности. При учете молекулярного строения таких систем можно ожидать, что явления, происходящих в них, описываются весьма похожими методами, поэтому становится очень актуальным вопрос о более глубоком изучении строения и свойств этих веществ на уровне наноструктур. В настоящее время можно провести компьютерное моделирование, которое позволяет получить достаточно точные предсказания свойств этих материалов.

В сегнетоэлектрическом теле расположение атомов вблизи точки фазового перехода мало изменяется [1]. Поэтому для описания природы сегнетоэлектрика рассматривалась система имеющая только ориентационные степени свободы.

Потенциал взаимодействия между электроном и диполем определяется по формуле:

 

 


где   K1, K2  и K3 — константы локальных ориентационных взаимодействий дипольного типа, которые для анизотропных систем отличаются друг от друга,   - вектор напряженности электрического поля, - дипольный момент ротатора, — угол между ротаторами, расположенными в узлах i, j, k и i’, j’, k’ решетки.  Причем учитываются только взаимодействия между ближайшими (соседними) ротаторами.  Приведенные константы взаимодействия подробно описаны в работе [2].

При моделировании предполагалось, что электрон располагается в центре ячейки решеточной модели Гейзенберга. Электрон взаимодействует только с ближайшими соседними  диполями и внешним электрическим полем, кроме того, при моделировании считалось, что на положение диполей также влияют  соседние диполи и внешнее поле, но не влияют электроны. Электрон передвигается «прыжками» из одной ячейки в соседнюю. Причем, согласно алгоритму Метрополиса, переход в другую ячейку осуществляется, если  энергия электрона уменьшается или вероятность перехода меньше случайного числа, сгенерированного компьютером.

Благодаря рассмотренному методу рассчитывается подвижность неосновных носителей в зависимости от  химического строения вещества и температуры. На рис.1. изображена графическая визуализация  нахождения сегнетоэлектрика (двумерный случай) и движения электронов при температуре ниже точки сегнетоэлектрического фазового перехода.

C:\Users\kgg\Desktop\ph\Начало движения эл-на.jpg

Рис.1. Графическая визуализация движения неосновных носителей в двумерном сегнетоэлектрике.

На рисунке стрелками изображены ориентации диполей сегнетоэлектрика, точками – положение движущихся электронов. При создании анимации наблюдается движение электронов влево (против вектора напряженности электрического поля).  Моделирование проводилось с учетом периодических граничных условий, начальное положение электронов задается случайным образом.

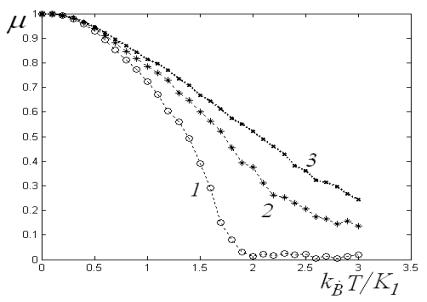
Рис. 2. Зависимости дальнего ориентационного порядка () изотропной сегнетоэлектрической системы от температуры при различных значениях напряженности внешнего электрического поля (кривая 1), 0,5 (кривая 2), 1(кривая 3)

На рис.2 приведены зависимости дальнего порядка от температуры при различных  значениях напряженности внешнего электрического поля. Как видно из рисунка, при определенной критической температуре параметр порядка резко падает, внешнее поле смещает точку фазового перехода и делает его более пологим.

Таким образом, с помощью компьютерного моделирования можно  воссоздать рассмотренный физический процесс и провести анализ полученных результатов, который показал, что на величину тока утечки в ферроэлектрике прежде всего влияет величина дальнего ориентационного порядка, который определяется  константами локальных ориентационных взаимодействий, температурой, напряжением внешнего электрического поля, а также наличием примесей.

Литература:

1.       Л.Д.Ландау. Теоретическая физика. Том VIII. М : Наука, 1982.

2.       А.В. Максимов, О.Г.Максимова. Высокомолек. соед. А. 2003. Т. 45. № 9. C. 1476-1468