Строительство и архитектура/ 3. Современные
технологии строительства, реконструкции и реставрации
Ст-т
Ведерников А.Н.; к.т.н. Кузнецова С.Г.
Пермский
национальный исследовательский политехнический университет
Зависимость
критической силы и податливости упругой опоры двухпролетной неразрезной
балки
Необходимо определить податливость упругой
опоры, обеспечивающей увеличение критического значения продольной силы в
заданное число раз.
Решим задачу методом перемещений. Очевидно, что
степень кинематической неопределимости равна 2. На рис. 1 приведена расчетная
схема и основная система метода перемещений соответственно
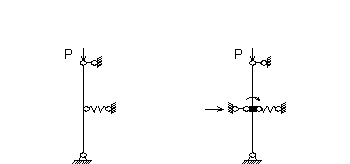
Рис. 1
На рис. 2 приведены
единичные эпюры метода перемещений
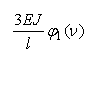
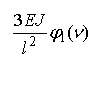
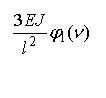
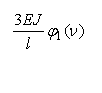
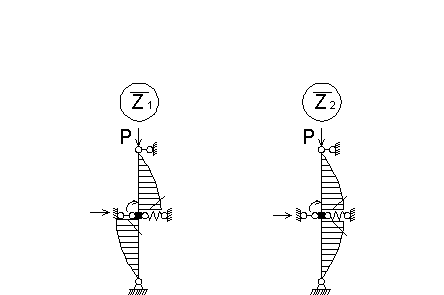
Рис. 2
Рассматривая равновесия узлов(рис. 3), найдем
коэффициенты канонических уравнений.
;
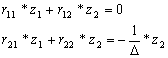
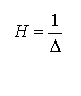
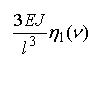
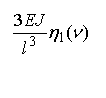
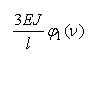
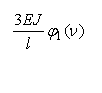
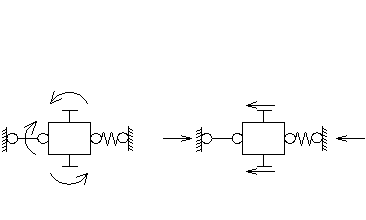
рис. 3
Второе уравнение системы
не равно 0, т.к. на месте введенной связи есть упруго податливая опора, в
которой и возникает усилие равное 
.
,
.
Получим уравнение устойчивости: 
. Вынеся
за скобку 
и, подставив
полученные нами ранее значения коэффициентов, получим:
. Решением
этого уравнения является:
……(1)
или
…….(2)
Из (1) имеем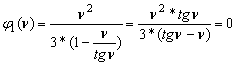 
, решением которого является
и следовательно 
, где 
- целое. Нас
интересует наименьшее значение осевой силы, поэтому 
. Тогда 
, что соответствует случаю, когда опора абсолютно жесткая,
т.е. 
и 
Из
(2): 
. Получаем 
, отсюда 
…...(3).
При отсутствии
промежуточной опоры имеем 
. Таким образом, из (3) получаем, что 
, т.е. 
, что выполняется при 
. Значит 
………(4). Из всего вышесказанного делаем вывод, что с помощью
податливой упругой опоры можно повысить критическую силу максимально в 4 раза,
а это значит, что 
……. (5), где «n» -
кол-во раз, в которое требуется повысить устойчивость стержня (n≤4).
Значение податливости упругой опоры можно найти из условия (3), с учетом (5).
Также можно подобрать такое значение податливости, при котором она будет вести
себя как абсолютно жесткая. Для этого достаточно в (3) подставить 
. Получим, что 
. Жесткость упругой опоры следует подбирать так, чтобы
податливость в точке контакта, как упругой опоры от действия единичной силы,
равнялась «
»
Библиографический список:
1. М.П. Сон, С.Г. Кузнецова. Строительная
механика зданий и сооружений. Спецкурс: учебное пособие / М.П. Сон, С.Г.
Кузнецова. – Пермь: Изд-во Пермского государственного технического
университета, 2009. – 185 с.