УДК 539.3

Ротко В.О., д.т.н. Шваб’юк В.І.

Луцький національний технічний університет, Україна

УТОЧНЕНА МОДЕЛЬ ЗГИНУ КОРОТКОЇ БАЛКИ З КОМПОЗИТНОГО МАТЕРІАЛУ

При створенні нових конструкцій, а також при реконструкції та підсиленні ушкоджених, на сьогодні все більшого застосування набувають композитні матеріали, зокрема, полімерні матеріали, армовані скляними, арамідовими чи вуглецевими волокнами [1]. Це дозволяє ефективно захистити конструкцію від дії агресивних середивищ, відтворити або навіть збільшити її жорсткість і міцність.

Дуже важливим при створенні композитів і їхнього застосування у конструкціях є поєднання процесів проектування конструкцій разом із матеріалом, що дає змогу забезпечити раціональність їх форм і технологічність виготовлення. Але за всієї різноманітності можливих форм зберігаються основні традиційні елементарні об’єкти, властиві для конструкцій найрізноманітнішого призначення. Це насамперед бруси (стрижні, балки), для яких використовують односпрямовані композити, волокна яких розташовують уздовж осі. Для брусів (стрижнів) різного призначення виникає потреба у проектуванні систем досить складних перерізів як за геометрією, так і за структурою матеріалів, серед яких, поряд із традиційними (метал, бетон, деревина), застосовують різноманітні штучні композитні матеріали. І якщо у системах композитних плит та оболонок неоднорідність структури виявляється у напрямку однієї з осей координат, то у композитних брусах неоднорідність виявляється як у формах їхніх перерізів, так і у структурі – у напрямку двох осей. Це значно ускладнює проблему врахування неоднорідності таких балок і моделювання їх напружено-деформованого стану.

Важливою особливістю орієнтованих композитів є незначна зсувна жорсткість – для більшості застосовуваних матеріалів модуль пружності на розтяг уздовж волокон і поперечні модулі пружності та зсуву значно відрізняються. Тому є необхідність урахування податливості композитних балок поперечним зсувам і обтисненню та впливу на них поперечних дотичних і нормальних напружень.

Виходячи з гіпотези плоских перерізів Бернуллі-Ейлера, диференціальне рівняння зігнутої осі балки має вигляд [1]:

. (1)

Тут — поздовжній модуль пружності матеріалу балки; переміщення середньої лінії балки; згинальний момент; момент інерції поперечного перерізу.

Рівняння (1) при згині балки не враховує складових прогину, які з’являються за рахунок впливу поперечної сили та поперечного обтиснення . Разом із тим, практично для всіх важливих конструкцій, додатковий прогин, викликаний поперечною силою, є співмірним із прогином від згинального моменту (особливо для балок із композитних матеріалів). Внаслідок зсуву та викривлення суміжних перерізів балки один відносно одного виникають додаткові переміщення .

Для визначення цих переміщень С.П. Тимошенко [2] використав закон Гука для чистого зсуву:

(2)

та формули для максимальних дотичних напружень у балці прямокутного поперечного перерізу:

(3)

або круглого поперечного перерізу:

, (4)

де і площі поперечних перерізів балки; поперечний модуль зсуву матеріалу.

Звідки:

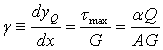. (5)

Тут - коефіцієнти зсуву відповідно для прямокутного та круглого перерізів, що відповідають найбільшому значенню кута зсуву на рівні серединного шару балки.

Диференціюючи вираз (5) за змінною х, одержали залежність для кривини балки від впливу поперечного зсуву:

, (6)

де - розподілене навантаження на балку.

Таким самим способом, як ураховувався поперечний зсув, можна знайти складову і від впливу поперечного обтиснення (зміни товщини балки при згинанні). Для цього необхідно про інтегрувати відповідну залежність із закону Гука:

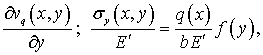(7)

де —закон розподілу нормальних напружень за товщиною [1]; — поперечний модуль пружності матеріалу; складова впливу поперечного обтиснення.

Проінтегрувавши вираз (7) за товщиною, одержимо

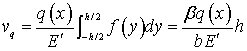, (8)

Тут , на основі досліджень [3], параметр .

Тоді, за аналогією до (1), на основі принципу суперпозиції, повний вираз для кривини пружної лінії балки можна записати у вигляді:

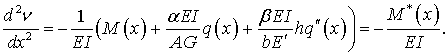(9)

Тут

Отже, у тих випадках, коли потрібно врахувати вплив поперечної сили та поперечного обтиснення на величини прогинів балки, необхідно замість рівняння (1) інтегрувати рівняння (9). Аналіз формули (9) показує, що поправка на прогини середньої лінії балки від впливу поперечного обтиснення можуть виникати тільки тоді, коли розподілене навантаження на балку є функцією від . Проте, вона може бути значною при визначенні переміщень зовнішніх шарів балок [3].

З сталої поперечної сили (), додаткове переміщення можна визначити також із диференціального рівняння (5):

У випадку згину консолі зосередженою силою стала , а повне переміщення вільного кінця консолі запишеться у вигляді:

(8)

Тут 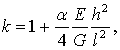а вплив поперечного обтиснення відсутній.

Для ізотропної балки (Е/G=2,6; l=10h) із прямокутним перерізом коефіцієнт , для таких самих дерев'яної (E/G = 20) і склопластикової балок коефіцієнти та , відповідно. Для короткої балки l=5h ці коефіцієнти будуть наступними: , , . Таким чином, фактор поперечного зсуву може стати суттєвим для величин прогинів у коротких композитних балках. У випадку зосереджених навантажень, а також при розв’язуванні контактних задач, вирішальну роль уже відіграє поправка від урахування впливу поперечного обтиснення [4].

_{Література:}

1. А.К.Малмейстер, В.П.Тамуж, Г.А.Тетерс.Сопротивление полимерных и композитных материалов. – 3-е изд., перераб. и доп. – Рига: Зинатне, 1980.

2. Тимошенко С.П., Дж. Гере. Механика материалов. Изд.-во «Мир» —М. 1976. С. 610.

3. Швабюк В.И. К теории изгиба коротких трансверсально-изотропных балок //Расчет пространственных строительных конструкций. Куйбышев: КуИСИ, 1981, в.9, с.86-91.

4. Шваб’юк В.І., Пастернак Я.М., Ротко С.В. Уточнений розв’язок задачі С.П. Тимошенка для ортотропної балки на жорсткій основі // Міжнародний наук.-техн. журнал: Фізико-хімічна механіка матеріалів. – Львів. – 2010. – Т.46. – № 1. ─ С. 51‑56.