К.т.н. Семенчев Е.А., Демидова А.В.

Тульский государственный университет, Россия

Интеллектуальная навигация в 3-d пространстве для универсальных беспилотных транспортных платформ

В настоящее время актуальны разработки автономных транспортных платформ (АТП) земного, воздушного, морского назначений, перемещающихся в динамически изменяющемся пространстве. Задача создания эффективных универсальных методов интеллектуальной навигации в реальном времени при перемещении АТП является актуальной, так как от ее решения зависит дальнейшее развитие безлюдных интеллектуальных машин и их широкое распространение в различных областях человеческой деятельности.

Проблемы, вызванные наличием в зоне перемещения АТП неизвестных заранее статических или динамических препятствий, обусловливают необходимость разработки методов планирования и управления перемещением в реальном времени. Суть данных методов заключается в том, что после получения АТП задания в ходе планирования в режиме реального времени происходит формирование допустимой траектории перемещения с учетом возможных конфигураций АТП и информации об окружающей среде, считанной датчиками. Далее, в процессе сканирования окружающего пространства генерируются все возможные траектории перемещения, с дальнейшим выбором оптимальной. Полученная траектория является задающим воздействием для управления, формируются соответствующие сигналы для изменения параметров движения робота, что гарантирует выполнение им безопасного перемещения с минимально возможной погрешностью достижения цели.

Целью исследования являлся поиск новых принципов построения и повышение степени универсальности алгоритмов автономного перемещения АТП в пространстве с препятствиями.

Метод декомпозиции свободного трехмерного пространства по двойственным парам.

Идея метода состоит в следующем. Осуществляется иерархическая декомпозиция свободного пространства по двойственным парам, образованным объектами с наименьшим расстоянием между ними в плоскостях ортогональных перемещению АТП. Текущее положение АТП принимается за действительный полюс двойственной пары, тогда как то место, куда она должна переместиться – за мнимую часть двойственной пары. Мнимая часть вычисляется благодаря двум другим двойственным парам, образованными концами виртуальной перекладины, соединяющей наиболее сближенные точки границы свободного пространства между препятствиями, как в вертикальной, так и в горизонтальной плоскости. Таким образом, мы получаем три пересекающиеся перекладины двойственных пар. Маршрут проходит примерно по «золотому числу» пересечения перекладин в плоскости ортогональной направлению движения. На каждом этапе перемещения процедура анализа и вычислений приобретает циклический характер. В основе нашего метода лежит принцип наименьшего действия и закон сохранения двойственных отношений. При наличии нескольких возможных маршрутов, декомпозиция принимает иерархический характер.

Анализ свободного пространства в направлении движения на некотором удалении от текущего положения в зоне видимости АТП и определение свободного от объектов пространства происходит с шагом m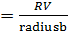, в плоскости ортогональной направлению движения.

АТП получает координаты целевой точки и начинает движение к ней по идеальному маршруту – по прямой, так как она является наименьшим расстоянием между двумя точками. В соответствии с принципом наименьшего действия наш объект движется по прямой с некоторой скоростью, но по этапам. На каждом этапе (интервале времени) происходит анализ ситуации. Если на пути попадается значительных размеров объект, границы которого не видны сенсорам, срабатывает алгоритм системы безопасности – двигаться вдоль объекта не ближе определенного безопасного расстояния.

С шагом равным radius получаем данные об окружающем пространстве в координатах (X, Y, Z) относительно сенсорной системы. Получаем матрицу вида:

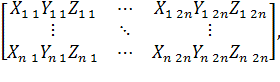
где 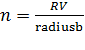, RV – размер области видимости, radiusb – размер безопасной зоны. При чем

;;

;

Полученные результаты соответствуют данным относительно сенсорного элемента, поэтому далее преобразовываем полученные координаты относительно центра объекта: , , .

Далее получаем m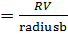 матриц следующим образом: осуществляем отбор только тех элементов матрицы, у которых значение координаты Z соответствуют неравенству:

Остальные элементы матрицы заменяются нулями.

В полученных матрицах в крайних столбцах и строках значения нулей заменяем на координаты , где i – номер строки, j - номер столбца. При чем:

;;

;

Это делается из-за того, что за границей области видимости могут располагаться объекты мешающие перемещению АТП, поэтому и предполагаем, что все пространство за зоной видимости является для АТП не проходимым.

В преобразованных матрицах для каждого шага Z_nm оцениваем возможность перемещения объекта.

Само вычисление координат точек дальнейшего перемещения объекта (маршрута) происходит следующим образом: на отобранных на предыдущем этапе взаимодополнительных крайностях свободного пространства определяются точки будущего положения АТП. Таким образом, мы получаем некоторое количество мнимых пар, крайностями которых являются текущее местоположение нашего объекта и мнимое место, где в дальнейшем он должен оказаться. Получив все возможные варианты крестообразующих двойственных пар, АТП выбирает наиболее оптимальный маршрут перемещения, основываясь на принципе наименьшего действия, т.е. выбирая маршрут наиболее близкий к целевому.

На втором этапе вычисляется значение предварительного шага перемещения АТП. Наше начальное положение имеет координаты , для перемещения получили точку

Угол поворота α рассчитывается по следующей формуле:

если и , то ,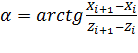

в противном случае .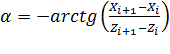

Шаг рассчитывается по следующим формулам:

если , то ;

если , то .

Полученные значения угла поворота и шага перемещения не должны превышать параметры skygol и R соответственно, в противном случае перемещение в данную точку пространства будет не возможно. В этом случае проверяем возможность перехода в точку с координатами , являющимися решением следующей системы:

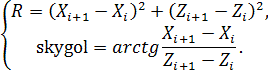
Далее оцениваем возможность перемещения в полученную точку для 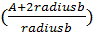матриц. Это необходимо из-за объемности нашей АТП. Таким образом, на всю глубину зоны видимости оцениваем возможность перемещения АТП в конкретную точку. После получения первой точки перемещения, операция оценки окружающего пространства повторяется для m матриц.

После получения m точек перемещения, в случае если маршрут может быть пройден, перемещаемся в точку с координатами и далее повторяем снова оценку окружающего пространства во всю глубину радиуса видимости. Полученный на этом шаге сценарий сравнивается с предыдущим. Если получаем различия выстроенных траекторий, можно сделать вывод о нахождении на траектории движения динамического препятствия. Это приводит к пересчету сценария перемещения.

В соответствии с изложенной схемой разработаны навигационный алгоритм и компьютерная имитационная модель перемещения АТП в модельных условиях.

Модульная структура имитационной программы представлена на рис. 1.

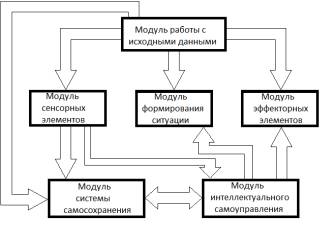
Рисунок 1 – Схема структуры имитационной программы навигации автономных объектов в пространстве с препятствиями

При разработке имитационной модели АТП принята симметричным объектом, в форме шара. В модели использовались следующие характеристики: оптимальная скорость АТП - R_, м/с; радиус АТП – A, м; скорость поворота АО – skygol, °/с; размер безопасной зоны – radiusb, м; задается в процентом соотношении к радиусу автономного объекта; размер области видимости – RV, м.

Каждый модуль имеет ряд функций.

Модуль работы с исходными данными - получение исходных данных для их последующего использования.

Модуль формирования ситуации - имитация окружающего пространства, создание объектов окружающего пространства различной конфигурации.

Модуль интеллектуального самоуправления - принятие решений об изменении параметров движения.

Модуль сенсорных элементов - слежение за потенциальными объектами внимания; получение параметров объектов внимания и характеристик их движения.

Модуль эффекторных элементов - определение параметров движения АТП; осуществление перемещения АТП.

Модуль системы самосохранения - анализ положения АТП относительно окружающего пространства; - изменение параметров движения; - подача сигнала тревоги.

Работа программы возможна в нескольких режимах: для объекта типа андроид (человекоподобный робот), типа робот, типа автомобиль, а так же для любого свободного типа объекта, параметры которого могут задаваться вручную.

При выполнении имитации происходит автоматическое заполнение бортового журнала, где фиксируются все изменения параметров движения АТП (рис. 2).

Рисунок 2 – Бортовой журнал

При стандартной симуляции траектория движения АТП уже изображена – прямая красная линия с точками на краях – начало и конец пути. Если запускается не стандартная симуляция данную траекторию нужно обозначить самостоятельно и только тогда АТП начнет движение. При стандартной симуляции так же возможно изменение траектории. Это осуществляется следующим образом – на желаемом месте окончания пути требуется двойным щелчком мыши обозначить точку окончания движения. После чего автоматически построится вся траектория движения. Во все время работы имитации есть возможность менять траекторию движения АТП.

После начала движения за АТП рисуется новая траектория его движения – зеленого цвета (рис. 3).

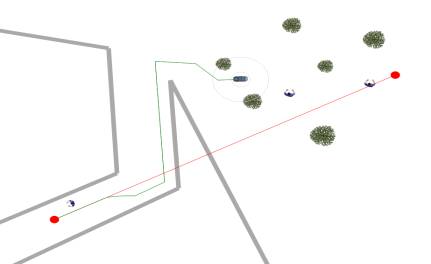
Рисунок 3 – Старая и новая траектория движения АТП (беспилотного автомобиля)

Таким образом, для решения актуальной научно-технической задачи был разработан метод маршрутизации и управления перемещением АТП в динамически изменяющемся пространстве. В ходе выполнения работы получены следующие результаты: предложен принципиально новый метод декомпозиции свободного пространства по двойственным парам; разработан универсальный управленческий алгоритм перемещения АТП в режиме реального времени в трехмерном пространстве в неизвестной динамической среде; предложена структура функциональной модели динамического планирования перемещения АТП.

Проведенные имитационные эксперименты с моделями АТП различного типа показали работоспособность предложенных алгоритмов маршрутизации и управления при движении в динамически изменяющемся пространстве.

Литература

1.Семенчев Е.А. Системный анализ и синтез искусственных живых машин: двойственный аспект: монография. – Тула: Изд-во ТулГУ, 2013.- 252 с.