Òåõíè÷åñêèå íàóêè/2. Ìåõàíèêà
D.tech.scien. Artamonova E.N.
Saratov State Technical University n.a. Gagarin Y.A., Russia
Analysis of soil bases
In this paper the
conditions for the modeling of facilities' ground bases are summarized. In
some models the V.Z Vlasov – N.N Leont'ev theory of calculation for ground bases is used. It
based on the fundamental equations of mechanics and the solution of
differential equations for the expected draft at the point.
In this study, subgrade strength variability and flexible
foundation and
pavement designs are evaluated for reliability. Reliability is an important factor design to consider the
variability associated with the design inputs. Parameters such as mean, maximum
likelihood, median, coefficient of variation, and density distribution function
of subgrade strength are determined [1]. The approach is based on an extensive
literature review of current damage concepts included in current
mechanistic-based design procedures, soil permanent deformation laboratory data.
Design outputs are compared in terms of reliability and thickness using these
design procedures. It is shown that the provides higher reliability values
compared to the probabilistic procedure. All the existing subgrades fail
distress reliability such as rutting and top down cracking reliabilities.
Currently uses a single design P value to deal with variability associated with subgrade strength
design.
Is used to generate full scale subgrades
response and performance data for development and verification of subgrades
design criteria. The physical
properties of subgrades structures significantly influence both the response of
the subgrades to applied loads and the long-term performance.It is, therefore,
of the utmost importance that full scale test subgrades be constructed with
uniformity in material properties, layer thicknesses, and other considerations
for which non-uniformity might result in nonrepresentative and nontypical
behavior and failures [1]. Current mechanistic-based design methods for
the design of subgrades use vertical
strain criteria to consider foundation rutting.
 A considerable number of measurements of the
physical properties test pavements were made at all stages of construction and
after construction was completed. The
measurements were made for three purposes: construction quality control,
construction acceptance, and material characterization. The material
characterization tests were performed to provide information for theoretical
modeling and were not related to construction and contractual
requirements.Tests were conducted on the subgrade materials, base subbase, and
surface layers. For
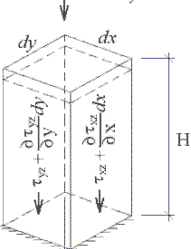
a basis of model building we take the model of elastic foundation, Vlasov - Leont'ev [1] (fig.1).
A considerable number of measurements of the
physical properties test pavements were made at all stages of construction and
after construction was completed. The
measurements were made for three purposes: construction quality control,
construction acceptance, and material characterization. The material
characterization tests were performed to provide information for theoretical
modeling and were not related to construction and contractual
requirements.Tests were conducted on the subgrade materials, base subbase, and
surface layers. For
a basis of model building we take the model of elastic foundation, Vlasov - Leont'ev [1] (fig.1).
figure 1
Here [2]:
u(x,y,z)=0; v(x,y,z)=0 ;
![]() (1)
(1)
![]() ;
; ![]() ;
;
D3=D1μ1+2Dk; Dk=Gh3/12.
Tests performed during construction consisted of
measuring insitu moisture content and
density. Tests were performed to characterize the variation of subgrade
strength with depth and over a tight horizontal grid. Width of the subgrade surface was divided into equally sized
quadrants and a location within each quadrant determined by randomly selected x
and y coordinates. The choice of
the appropriate type
of foundation is
governed by some important
factors such as: the
nature of the structure; the loads exerted by the structure;
the subsoil characteristics;
the allotted cost of foundations. Therefore to decide about the type of foundation,
subsoil exploration must be carried out. Then the soil characteristics within
the affected zone below the building should be carefully evaluated. The
allowable bearing capacity of the affected soil strata should then be
estimated. Theory of elasticity analysis indicates that the
stress distribution beneath footings, symmetrically loaded, is not uniform.
The actual stress distribution depends on the type of material beneath the
footing and the rigidity of the footing. For footings on loose cohesion-less
material, the soil grains tend to displace laterally at the edges from under
the load, whereas in the center the soil is relatively confined.It is shown in this study that single design strain value for a roadway section does
not yield an effective design regarding target reliability [2].
References:
1. Petrov V.V. Dimensional model of nonlinear deformable heterogeneous base // Interuniversity scientific collection.- Saratov: SSTU, 2007.- P.6-12.
2. Artamonova
E.N. On the design of slabs on the basis of a non-uniform // Moskau: INGN, 2012.- P.4.
In this paper we propose a
mathematical model of destruction (the relations connecting parameters
of efficiency at the time of fracture characteristics material), based on the
relationship of both these approaches to allow for the dependence of the
limiting critical conditions at which the destruction, the time of stress,
temperature environmental exposure, exposure, etc. This is especially typical
for polymers [1]. An examination of these experimental data one can draw
conclusions that should be taken into account when constructing the
mathematical correlations for the conditions of fracture:
Mechanical properties and the process of destruction of polymer
materials substantially depend on time and operating conditions.
Destruction is a two-stage process. At the first stage the
degradation of the properties of the material, the accumulation of damage,
microcracks occur. The stage ends at a time when the merger of microdamage
formed macroscopic crack. This moment is short-lived and by their physical
nature is a loss of stability of equilibrium microdefects.
Because of the irreversibility of
the process of destruction is determined not only the current values of
parameters characterizing it, but the entire prior history change of these
parameters.
Because of the private nature of the experimental data on the
effect of medium on behavior of plastic the composition of the general
mathematical for all materials the
phenomenological description of fracture based on mechanical ideas due to the
difficulties and serious shortcomings. Therefore it is necessary and the molecular interpretation
of macroscopic changes in the material. Thus, the phenomenological theory of
time dependence as would provide a common framework, which must fit the theory
of material behavior, and that put a detailed mechanical theory of change of macroscopic
and microscopic properties of the polymer. This need arises in the
interpretation of the parameters of the phenomenological equation, allowing you
to identify not only the common features, as well as the difference between the
materials.
Because of significant time effects for polymers the process of
their destruction more difficult than traditional materials, the phenomenon of
viscous and brittle fracture occur simultaneously. Fracture criterion in this
case must take into account the achievement σ, ε of the
instantaneous and destructive values σ
ð, ε ð, at the time tðàçð.,
and their dependence on the development of degradation of material properties ω (t).
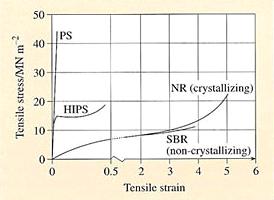
Figure
1.
Analysis of experimental data (Fig.1) suggests characteristics of
the temperature dependence of relaxation processes and fracture for
viscoelastic polymers with the same value of energy activation for each material.Both aspects of the strength of
polymers depend on the local structural changes that primarily can be linked
with the process of accumulation of damage, education grid hairline cracks.
Combining different approaches to describing these processes, i.e. formulation
of a general mathematical theory of deformation and fracture of polymers
depends on the study of the relationship of deformation, destruction and action
of strain, temperature, aggressive factors in the whole time interval of
operation of the element.
According the survey of the literary
sources for the analyzing of long-term durability of materials and elements
made of them two alternative approaches are basically exist: mechanical
(benchmarking) and kinetic.
According the first approach we
model the generalized condition for material destroying:
Ô
(θ1, θ2, θ3 ) = Ô ð.
Here Ô - the functional is some combination of the components of the stress or strain. The functional
Ô depends on the accepted theory strength or
given empirically and then the functional contains parameters determined
experimentally.
Ô = ∫dV [1/2 ρu?iu?i–
λ/2 ∂ui/∂xi ∂uj/∂xj - µ/2( ∂ui/∂xj
∂ui/∂xj +
∂ui/∂xj ∂uj/∂xj)].
1.The strain tensor can be
represented as a sum of tensors of elastic deformation of inelastic
deformation:
ε ij = ε
ij¹ + ε ij².
2. For description the strain state
and fracture in the framework of a generalized model of inelasticity is
necessary to consider the history of deformation of the sample depends on the
loading path and on time. For different loading paths for the processes of
varying duration results will be different.We give a physical explanation of
the above stated hypothesis.
References:
1. Suvorova J.V., Ohlson N.G., Alexeeva
S.I. An approach to the description of time-dependent materials //Materials and
Design, Vol.24. Issue 4, June 2003.- P.293-297.