Технические науки/4. Эксплуатация водного транспорта, судовождение

Д.т.н. Юдин Ю.И., аспирант Иванов В.В., аспирант Грабаровский А.Б.

Мурманский государственный технический университет, Россия

Составляющие воздействия нерегулярного волнения

Реальное морское волнение является нерегулярным, так как в совокупности представляет собой волны с различными значениями их геометрических параметров и частотных характеристик.

Будем считать, что при этом все усилия, образующиеся на корпусе судна при плавании на волнении, представляют собой стационарные случайные процессы в условиях заданной спектральной плотность волнения. Это может быть спектральная плотность амплитуды волны, высоты волны или угла волнового склона. Все эти спектральные плотности одинаковы, и для конкретности мы будем использовать спектральную плотность амплитуд волнения S_zw (w_w) (z_w – амплитуда волновых ординат;w_w – частота волнения). Поскольку все усилия линейно связаны с самим процессом волнения, то для нерегулярного волнения можно подсчитать среднее значение и дисперсию любого усилия по известным интегральным формулам [1, 3]:

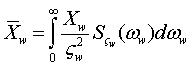
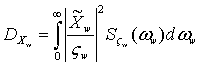, (1)

где - центрированное значение усилия, т.е. разность между самим усилием и его средним значением.

Формулы (1) приведены для продольного усилия X_w; формулы для поперечного усилия и вращающего момента имеют точно такую же структуру. Главным здесь является спектральная характеристика амплитуды волнения S_zw(w_w). Конкретные расчёты выполнены для нерегулярного двумерного волнения, в котором смешаны две составляющие – высокочастотная S₁ и низкочастотная S₂ в виде двух слагаемых. Обе составляющие записаны далее для высоты волны 3%-ой обеспеченности h_3%= 3 м и представлены графически на рис. 1 как функции частоты w_w. Сами спектральные плотности для h_3%= 3м известны из работы [4] и выглядят аналитически следующим образом:

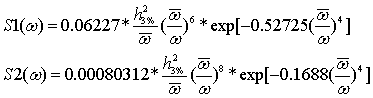(2)

где = 1.1 с^-1- средняя частота нерегулярного двумерного волнения для выбранной высоты волны h_3%.

Применяя формулу (1) для среднего значения путём интегрирования находим среднее значение поперечного усилия в зависимости от курсового угла нерегулярной волны q_w (рис. 2). Отдельно показаны усилия, генерируемые двумя слагаемыми спектральной плотности волнения S₁ и S₂.

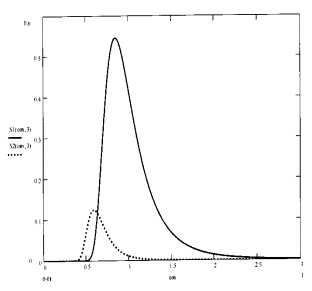
Рис. 1. Слагаемые спектральной плотности нерегулярного волнения с h_3% = 3 м: высокочастотная (S₁) и низкочастотной (S₂).

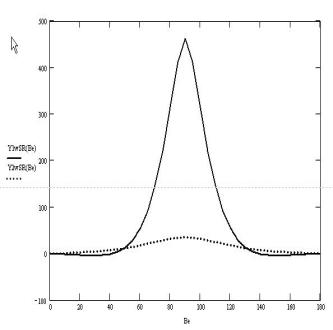
Рис. 2. Средние значения поперечного усилия на корпусе танкера (кН) в зависимости от курсового угла нерегулярной волны с h_3%=3 м для высоко частотной и низкочастотной слагаемых волнового спектра.

Аналогичный график для среднего значения вращающего момента представлен на рис. 3.

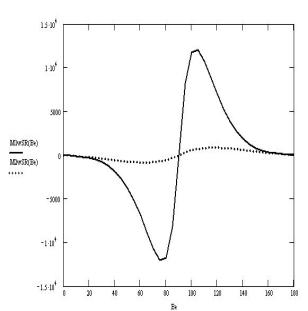
Рис. 3. Средние значения вращающего момента (кН´м) в зависимости от курсового угла нерегулярной волны с h_3%=3 м для высоко частотной и низкочастотной слагаемых волнового спектра.

Среднеквадратические (стандартные) отклонения поперечного усилия и вращающего момента, также вычислены и представлены на рис. 4 и 5.

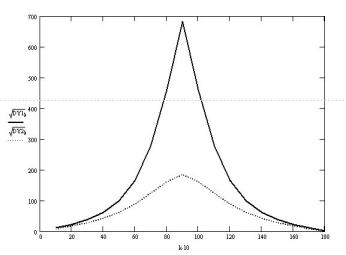
Рис. 4. Стандартные отклонения поперечного усилия (кН) в зависимости от курсового угла нерегулярной волны с h_3% = 3 м, для высокочастотной и низкочастотной слагаемых волнового спектра.

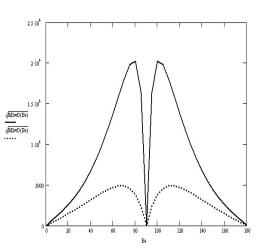
Рис. 5. Стандартное отклонение вращающего момента (кН´м) в зависимости от курсового угла нерегулярной волны с h_3%=3 м.

Аналогичные вычисления произведены для продольного усилия и представлены на рис.6 и 7.

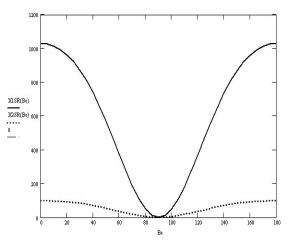
Рис. 6. Среднее значение продольного усилия (кН) в зависимости от курсового угла нерегулярной волны с h_3%=3 м

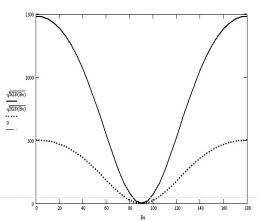
Рис.7. Стандартное отклонение продольного усилия (тс) в зависимости от курсового угла нерегулярной волны с h_3% = 3 м.

Представленные в настоящем докладе результаты расчётов продольной и поперечной составляющих усилий и момента вращения на корпусе танкера, подверженного воздействию нерегулярного волнения, подтверждают возможность использования разработанного автором алгоритма расчёта указанных параметров для компьютерного моделирования процесса поведения судна при действии нерегулярного волнения.

Литература

1. Хаскинд М.Д. Теория сопротивления при движении судна на волнении/ М.Д. Хаскинд // Изв. АН СССР – 1959 - №2,- С.46-56

2. Хаскинд М.Д. Гидродинамическая теория качки корабля/ М.Д Хаскинд. - М.: Наука, 1973 – С. 327.

3. Войткунский Я.И. Справочник по теории корабля, т. 1 /под ред. Я. И. Войткунского– Л.: Судостроение, 1985 – С.762

4. Войткунский Я.И. Справочник по теории корабля, т. 3 /под ред. Я. И. Войткунского– Л.: Судостроение, 1985 – С.541

5. Благовещенский С.Н. Качка корабля. Л.: Судпромгиз, 1954, - С.520.