Использование прикладных программ на уроках математики

Бейсенова Д.Р. – Карагандинский государственный университет им. Е.А.Букетова,

Мусабекова Р.Е. – общеобразовательная школа №16 г. Караганды.

Неотъемлемой и важной частью современных информационных процессов является компьютеризация образования. Проблема широкого применения компьютерных технологий в сфере образования в последнее десятилетие вызывает повышенный интерес в отечественной педагогической науке.

Вопреки расхожему мнению о том, что использование компьютерных средств будет способствовать стремлению учащихся меньше изучать теорию, они будут хуже решать задачи без помощи машин, именно постоянное их применение даёт импульс к изучению методов, заложенных в программах. Компьютерные программы хорошо работают только под управлением умелых пользователей. Например, использование программ решения уравнений даже в самых мощных математических пакетах далеко не всегда с первой попытки позволяет найти их корни, не говоря об их полном множестве. Поэтому опасения, что компьютеры будут решать задачи за школьников, а последние будут учиться без должного прилежания, совершенно беспочвенны. К сожалению, в школьной практике нет возможности использовать такие мощные математические пакеты, как Mathematica, Mathcad, MathLab, Maple из-за дороговизны их лицензионных копий. Однако офисные приложения MS Office есть в каждой школе. Не все знают, что применение математической оболочки офисного табличного процессора MS Excel позволяет решать математические задачи высокой трудности.

Применение MS Excel необходимо при изучении следующих разделов математики:

- построение графиков функций;

- изучение свойств функций;

- преобразование графиков функций;

- решение уравнений и систем уравнений;

- решение уравнений способом «Поиск решений».

Например, в Excel можно решать систему линейных уравнений.

Система линейных уравнений с неизвестными имеет вид:

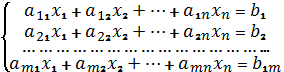
Здесь и – заданные числа, которые называются соответственно коэффициентами при неизвестных и свободными членами.

Для того чтобы представить систему линейных уравнений в матричном виде, коэффициенты при неизвестных представляют в виде матрицы

A=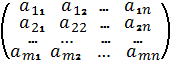

Матрица А называется матрицей системы.

Свободные и неизвестные члены представляются в виде матриц-столбцов

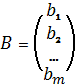
В матричной форме система линейных уравнений записывается в виде .

В частном случае, когда число уравнений в системе ( равно числу неизвестных , т.е. , то решение такой системы можно найти методом обратной матрицы в виде , где - матрица, обратная по отношению к исходной матрице .

Пример. Пусть имеется неоднородная система линейных уравнений (т.е. свободные члены отличны от нуля)

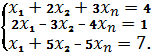
Решим эту систему матричным методом.

,

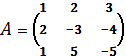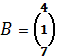
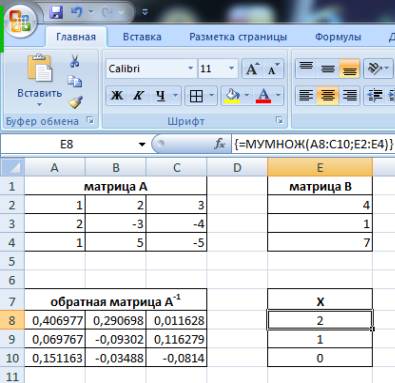
Итак, решение этой задачи в Excel с ввода двух мариц А и В.

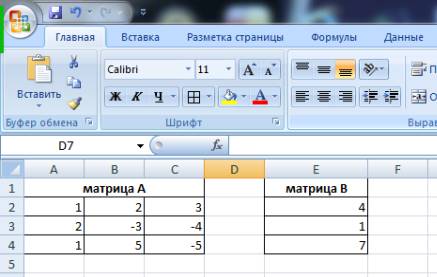
Искомое решение будет находиться по формуле: .

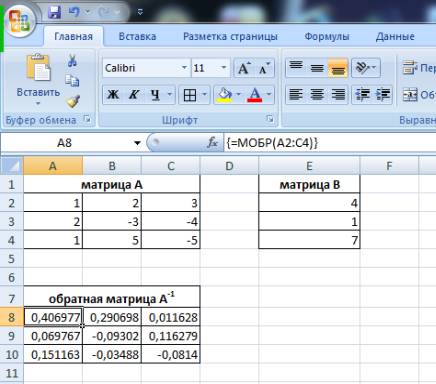
Для его нахождения необходимо выполнить следующие действия: найти обратную матрицу при помощи функции МОБР из категории Математические (перед вводом функции необходимо выделить диапазон, содержащий достаточно ячеек для размещения всех результатов, после завершения ввода формулы нажмите клавиши <Ctrl>+<Shift>+<Enter>).

C использованием функции МУМНОЖ выполнить перемножение матриц и , в результате получим искомое решение:

Таким образом, использование компьютерных технологий на уроках математики позволяет реализовывать следующие цели процесса обучения:

- повысить качества знаний по теме;

- продолжить формирование информационной культуры;

- наиболее полно реализовать учебные возможности каждого ученика.

Основные достоинства компьютера для целей обучения следующие [1]:

- компьютер является наиболее адекватным техническим средством обучения, поддерживающим деятельностный подход к учебному процессу во всех его звеньях;

- компьютер может принимать роль активного партнера и тем самым стимулировать активность учащегося;

- программируемость учебного процесса в сочетании с динамической адаптированностью содействует индивидуализации учебного процесса;

- контролируемость учебного процесса в сочетании с гибкостью пользовательского интерфейса делает компьютер идеальным средством тренировок;

- внутренняя формализуемость работы компьютера, «правил игры», способствует большей осознанности процесса, повышает его интеллектуальный и логический уровень;

- способность компьютера к построению визуальных и других сложных образов существенно повышает пропускную способность информационных каналов учебного процесса;

- компьютер вносит в учебный процесс принципиально новые познавательные средства, в частности вычислительный эксперимент, решение задач с помощью экспертных систем, конструирование алгоритмов и пополнение баз знаний;

- являясь ведущим и массовым инструментом новых информационных технологий, компьютер самим фактом органичного включения его в учебный процесс, сближает сферу обучения с реальным миром;

- свойства универсальности и программируемости способствуют многоцелевому применению компьютера.

Использованная литература:

1. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: учеб. пособие. М.: Финансы и статистика, 2002.

2. Гельман В.Я. Решение математических задач средствами Excel: практикум. СПб: Питер, 2003.

3. Ефимова О., Морозов В., Угринович. Курс компьютерной технологии с основами информатики. Учебное пособие для старших классов. – М.: ООО «Издательство АСТ», 2000.

4. Ильченко А.Н. Экономико-математические методы: учеб. пособие. М.: Финансы и статистика, 2006.

5. Информационно-компьютерные средства в школе: Методическое пособие / Под ред. проф. Г.К. Селевко. – Ярославль: ИРО, 2003.