Евсеев В.И.,
канд. физ.-мат. наук, доцент, г. Казань, РТ, Россия
Основные понятия трехзначной «мягкой» логики
Аннотация:
В работе изучаются
основные свойства отделяющих функций «мягкой» модели трехзначной логики, а
также определенные в ней унарные операции.
Ключевые слова: «мягкая»
модель, основные логические классы, условная ортогональность, условная
идемпотентность, унарные операции.
Summary:
in
this paper, we study the basic properties of separating the functions of the
soft model of three values, as well as operations in identified unary logic.
Keywords:
'sweet'
model, the classes of logical basis, conditional orthogonality, conditional
Idempotence, unary operations.
1.
Основное уравнение и
отделяющие функции в ![]()
В этих заметках мы
продолжим изучение «мягкой» модели трехзначной логики, начатое нами в [2]. Саму
эту модель обозначим ![]() , ее отделяющими
функциями
будут уже указанные в цитированном источнике значения, построенные на базе
основного уравнения этой системы:
, ее отделяющими
функциями
будут уже указанные в цитированном источнике значения, построенные на базе
основного уравнения этой системы:
![]() (1)
(1)
В данном случае
логические классы обозначены: ![]() ,
, ![]() – логический параметр этой системы,
– логический параметр этой системы, ![]() – значения логического параметра на
соответствующих классах истинности.
– значения логического параметра на
соответствующих классах истинности.
При этом отделяющие
функции принимают значение единица
только на своем классе, а на двух других равны нулю.
Таким образом, мы
получаем следующие выражения для
отделяющих функций этой трехзначной системы:
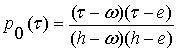 ,
(2)
,
(2)
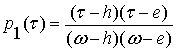 ,
(3)
,
(3)
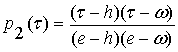 .
(4)
.
(4)
Теперь изучим основные свойства этих функций.
2. Основные свойства отделяющих функций.
Прежде всего, введем понятие главного определителя «мягкой
системы». В данном случае он имеет вид:
![]() .
(5)
.
(5)
Так как мы предполагаем,
что все три значения отделяющих функций
различны, и ![]() , то этот определитель строго положителен. Этот определитель
входит во многие формулы данной системы.
, то этот определитель строго положителен. Этот определитель
входит во многие формулы данной системы.
Теперь рассмотрим
основные свойства отделяющих функций.
Полнота системы, она
характеризуется основным условием:
![]() .
(6)
.
(6)
На этом
примере покажем, как проводятся доказательства утверждений с использованием
главного определителя системы.
Так, здесь получаем:
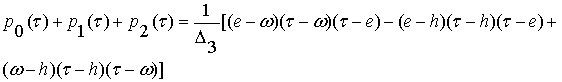
Преобразование заключается в том, что нужно
собрать в квадратных скобках значения при второй и первой степенях параметра ![]() , а также свободный член этой формулы:
, а также свободный член этой формулы:

Ясно, что значения первых двух скобок равны
нулю, а последние слагаемые дают как раз значение главного определителя, хотя в
несколько иной форме.
Таким образом, это свойство доказано.
3.
Условная
ортогональность отделяющих функций.
Условная ортогональность отделяющих функций заключается в том,
что для них произведение любой пары различных отделяющих функций выражается в
виде произведения функции основного уравнения системы ![]() на некоторую линейную функцию, мы ее будем называть весом ортогональности.
на некоторую линейную функцию, мы ее будем называть весом ортогональности.
Так, для произведения первых двух отдаляющих
функций получаем:
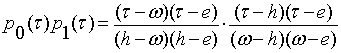 .
.
После небольших
преобразований с учетом неоднократных перемен знаков получим окончательную
формулу:
 (7)
(7)
здесь
![]() ,
(8)
,
(8)
это – весовая функция данной условной
ортогональности.
Для двух следующих случаев приведем только
окончательные результаты.
Так, для произведения нулевой и второй отдаляющих функций получаем:
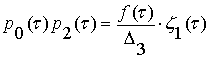 ,
(9)
,
(9)
где весовая функция
![]() . (10)
. (10)
Аналогично, для произведения первой и второй
отделяющих функций приходим к результату:
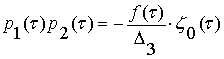 .
(11)
.
(11)
Здесь значение весовой функции следующее:
![]() .
(12)
.
(12)
4. Условная идемпотентность отделяющих функций.
Условная идемпотентность представляет собой
взаимосвязь между квадратом и первой степенью отделяющей функции. Общая формула
для всех отделяющих функций имеет вид:
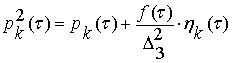 , (13)
, (13)
здесь ![]()
Весовые функции в этом случае также линейные,
они имеют вид:
![]() ,
(14)
,
(14)
![]() ,
(15)
,
(15)
![]() .
(16)
.
(16)
5. Отделяющая функция для инверсии.
В
трехзначной логической системе имеется две унарные операции:
инверсия как симметрия относительно класса
неопределенности ![]() , которая характеризуется таблицей переходов классов:
, которая характеризуется таблицей переходов классов:
|
|
|
|
|
|
|
|
|
|
А также логический сдвиг
(транш), при котором классы истинности переходят последовательно друг в друга:
|
|
|
|
|
|
|
|
|
|
В случае инверсии мы получаем переход от
суждения
![]() , (17)
, (17)
к его инверсии
![]() . (18)
. (18)
При этом
![]() – значение логического параметра для данного суждения.
– значение логического параметра для данного суждения.
Для инверсии в результате вычислений получаем
формулу:
![]()
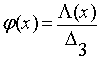 ,
(19)
,
(19)
здесь
квадратичная функция инверсии имеет вид:
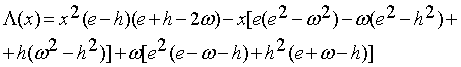 (20)
(20)
Для конкретных значений логического параметра
находим:
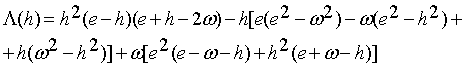 (21)
(21)
После раскрытия скобок и приведения подобных
членов окончательно получим:
![]() ,
,
значит,
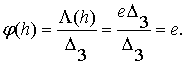
Аналогично, получаем для двух других случаев
соответствие с таблицей.
6. Отделяющая функция для логического сдвига
Формула для суждения после выполнения
логического сдвига:
![]() . (22)
. (22)
Поэтому функция истинности принимает вид:
![]() . (23)
. (23)
Эту функцию в общем случае представим через
главный определитель:
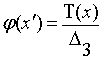 .
(24)
.
(24)
При этом квадратичная функция транша ![]() имеет вид:
имеет вид:
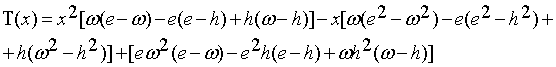 (25)
(25)
Эта формула точно соответствует таблице для
логического сдвига.
Проверку результатов,
которая здесь сложностей не представляет, мы оставляем нашим пытливым
читателям.
В следующих наших
работах мы планируем перейти к бинарным операциям конъюнктивного типа для
трехзначной «мягкой» логической системы.
Литература:
1. Евсеев В.И.
Конструктивная комплементарная семантика. Монография. Изд-во «Ламберт». 2014 г.
2.
Евсеев
В.И. О бинарных операциях в многозначных логиках//Материалы Х международной
научно-практической конференции «Образование и наука ХХI века», т. 11, 2014,
София, «Бял ГРАД-БГ» ООД, (31 – 47) .