Математическое моделирование уравнения баланса влаги в атмосфере

Н.С.Заурбеков (зав.каф. ИТ, д.т.н., проф., АТУ),

Шарипова Б.Д. (к.э.н., доцент, АТУ),

Н.Д.Заурбекова (к.т.н., зав.лаб., КазНТУ им. К.Сатпаева),

А.Е.Кутелов, Г.О.Сеитбекова (магистранты ИС, АТУ)

agu_nurgali@mail.ru

Моделирование реальной атмосферы с применением уравнений гидротермодинамики требует привлечения влажности как одного из важнейших параметров природы. Помимо проблемы включения фазовых процессов в гидротермодинамические уравнения, здесь уделено внимание к представлению в уравнениях движения массовых сил и на возможность исключения предположения о равенстве нулю горизонтальных градиентов потенциала силы тяжести.

Уравнения движения реальной атмосферы в поле массовых сил. Особенностью учета орографии в численных моделях является то, что он тесно связан с включением горизонтальной неоднородности массовых сил посредством определения потенциала силы тяжести в реальной атмосфере. Возьмем уравнения движения в векторной форме Громеко-Ламба для системы координат, вращающейся вместе с Землей:

где вектора: – угловой скорости вращения Земли; D – диссипативных сил; G=G(,,)– ускорения силы тяжести; V=V(,,)– скорости; а ,, – компоненты вектора скорости по осям криволинейной системы координат , , :

, ;

, .

Введем в качестве дополнения до геодезической широты , тогда будет геодезической долготой , а направим по нормали к эллипсоиду Земли. Расстояние любой точки M от ее проекции на поверхность эллипсоида будем измерять высотой . Связь абсолютных координат с вновь введенными осуществляется посредством следующих формул:

x=[а()sin+sin]cos;y=[а()sin+sin]sin;z=а()Cos+cos, (1)

где =() – дополнение до геодезической широты. Разность между геодезической и географической широтами представляется формулой:

- = - arctg[] , (2)

а коэффициенты Ламэ можно записать в следующем виде:

a() (,); =a() (,) Sin; = 1, (2`)

где = , .

Воспользовавшись (1) и (2), для , получим:

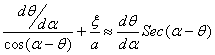= ; = . (3)

Предложенная система координат ортогональна (jk), где =x, =y, =z.

Если за эту поверхность принять явно эллипсоид вращения, то все формулы приводится более простому виду:

x =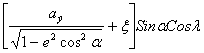; y =;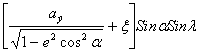

z =.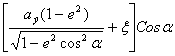

В эти формулы входят два параметра, определяющие эллипсоид: – радиус Земли в плоскости экватора и квадрат эксцентриситета 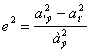. Эксцентриситет легко можно выразить через другую удобную характеристику эллипсоида – через сжатие S 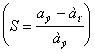следующим образом: . Найдем радиус-вектор точки (a). В меридиональном сечении для эллипсоида имеем: K = ; OK = 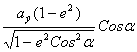,откуда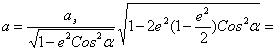

.

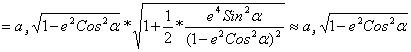Тогда, . (4)

Связь между геоцентрической и геодезической широтами осуществляется посредством выражения: .

Дифференцируем это выражение по , кроме того, из (2) следует:

, (5)

а также известно из [1] .

Тогда , и подставляя сюда (5) и используя (4), получим:

.

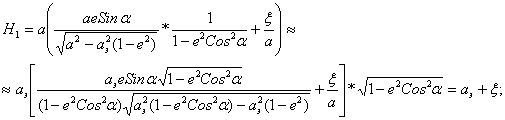
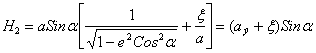Итак, в практических задачах решение (2) с коэффициентами Ламэ из (2`) представляют определенные трудности, а нами для коэффициентов Ламэ получены, с точностью до величин , очень простые выражения, по форме совпадающие с коэффициентами Ламэ для сферы. Полученные уравнения удобно использовать при описании движения реальной атмосферы в поле массовых сил и при определении связи между геоцентрической и геодезической широтами для объективной оценки экологической обстановки окружающей среды.

Учет неровностей земной поверхности. Наличие реального рельефа вызывает ряд технических трудностей при представлении в конечных разностях уравнений гидротермодинамики вблизи нижней границы атмосферы. Для преодоления этих трудностей обычно вводят новую систему координат, в которой нижняя неровная поверхность переходит в плоскость (или эллипсоид, сферу). Это достигается тем, что новые координаты трансформирует поле только по одной переменной (), оставляя его в остальных направлениях неизменным. Рассмотрим уравнения движения в результате преобразования координат. Для этого введем новые координаты, связанные со старыми следующими соотношениями: , , , . Выражения градиента массовых сил в новой системе координат имеет вид:

.

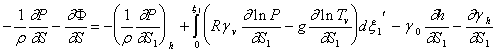Следовательно, применение “выпрямленных” координат вводит в уравнение дополнительный член, учитывающий орографию. Хотя это слагаемое велико, но оно компенсируется в значительной степени барическим градиентом, взятым вдоль земной поверхности. Таким образом, уравнения горизонтального движения можно окончательно представить в следующем виде (используются сферические координаты ):

;

,

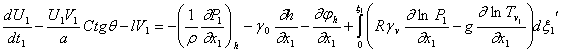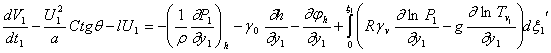где , , ;

.

Литература:

1. Айдосов А., Заурбеков Н.С. Теоретические основы прогнозирования природных процессов и экологической обстановки окружающей среды. Книга 3. Теоретические основы прогнозирования атмосферных процессов, экологической обстановки окружающей среды и построение геоэкологической карты на примере КНГКМ. А., Қазақ университеті, 2000. – 219 с.