УДК 615.47

МОДЕЛИРОВАНИЕ ПОЛЯ ГЕНЕРАТОРА АППАРАТА ЦИРКУЛЯЦИИ БИОЛОГИЧЕСКИХ ЖИДКОСТЕЙ

Корнилова Н.В, Щербаков М.А.

Аннотация: В статье описывается программный продукт, который предназначен для вычисления основных параметров генератора электромагнитных полей аппарата циркуляции биологических жидкостей. Приводятся результаты моделирования для одной секции.

Ключевые слова: моделирование, программный продукт, генератор, электромагнитное поле, катушка.

MODELING FIELD GENERATOR MACHINE CIRCULATION BIOLOGICAL FLUIDS

Kornilovа N.V., Shcherbakov M.A.

Abstract: The article describes a software product that is designed for calculation of the main parameters of the generator of electromagnetic fields apparatus circulation of biological liquids. Modeling results for one section.

Keywords: modeling, software, generator, electromagnetic field, coil.

Работа аппарата циркуляции биологической жидкости, основывается на управлении секциями генератора электромагнитных полей, представляющего собой семисекционную многослойную цилиндрическую катушку. Первая и седьмая секции управляют работой входного и выходного клапанов, а секции со второй по шестую – электрогидравлическим насосом. Роль поршня насоса и заслонки клапана выполняет магнитожидкостный элемент (МЖЭ), представляющий собой упругую оболочку из силиконовой резины, заполненную магнитной жидкостью.

При подаче управляющего напряжения на одну из секций формируется волна МЖЭ. Подавая последовательно управляющие напряжения на секции обмоток, волна будет плавно перемещаться. Если проточная часть насоса заполнена жидкостью, то волна МЖЭ будет выполнять функцию поршня для ее перекачивания [1,2].

Разработанный на языке Lazarus программный продукт служит для вычисления основных параметров генератора электромагнитных полей, в частном случае – семисекционного исполнительного элемента.

Исходными данными являются величины тока и напряжения, подаваемые на индуктивный элемент, а также конструктивные параметры катушки, такие как: ширина секции, их количество, внутренний и внешний радиальные размеры секции, а также число витков одной секции и диаметр поперечного сечения обмотки.

В результате выполнения программы выходными данными являются напряженность магнитного поля, вектор магнитной индукции, векторный потенциал, а также координаты точки Q(zq,rq) в которых данные параметры достигают максимального значения.

В главном окне приложения располагаются основные компоненты, при помощи которых производится расчет параметров семисекцонного исполнительного элемента. Пользовательский интерфейс программы с указанием полей ввода и вывода представлен на рисунке 1.

Установка размеров катушки осуществляется при помощи соответствующих полей. При указании размеров следует помнить о корректности ввода параметров геометрических фигур, однако, если пользователь допустит ошибку, то на экран будет выведено соответствующее сообщение с указанием того, каким образом она может быть исправлена или в каком месте параметры не соответствуют реальным.

При указании пользователем размера внутреннего радиуса катушки больше внешнего на экран выводится предупреждающее сообщение, после чего значение должно быть изменено на стандартное.

Рис. 1. Базовый интерфейс программы

Если неверно указано количество секций в индуктивном элементе, например не целое значение, то на экране также появится сообщение об ошибке (рис.2).

Рис. 2. Сообщения об ошибках размера радиуса и о количестве секций

Программа моделирования позволяет проводить анализ электромагнитного поля индукционного элемента, включающий расчеты основных параметров поля при различных конструктивных размерах и воздействиях.

За «эталонный» элемент была взята семисекционная цилиндрическая катушка со следующими параметрами: b=0,02м – ширина катушки; b₁=0.02м – первая осевая координата торца; b₂=0,04м – вторая осевая координата торца; R_н=0,04м – наружный радиус прямоугольного сечения катушки; R_В=0,02м – внутренний радиус прямоугольного сечения катушки; I=10А – максимальный ток катушки; N=200 – количество витков в одной секции; d=0,001м – диаметр провода обмотки катушки.

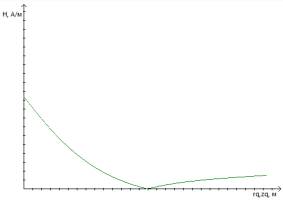
Результаты точечного моделирования сведены в таблицу 1, а также отображены в виде графика и диаграммы (рис.3).

По полученным результатам видно, что магнитная индукция в центре катушки приблизительно равна нулю.

Таблица 1 - Расчетные данные поля на поверхности магнитожидкостного

элемента

Координаты точки наблюдения: zQ;rQ, м	Составляющая векторного потенциала, Аφ^.10^-4, Вс/м	Вектор магнитной индукции, В^., Тл	Напряженность магнитного поля, НА/м
1	2	5	6
0,02; 0,0045	-1,8	0,37	4295
0,015; 0,0035	-1,59	0,35	4052
0,012; 0,002	-1,38	0,32	3741
0,015; 0,001	-1,23	0,3	3638
0,01; -0,0015	-2,87	0,48	5372
0,009; -0,002	-2,62	1,31	14671
0,0085; -0,0025	-2,46	1,98	22643
0,0075; -0,0035	-3,57	2,74	31123

Максимальные же значения достигаются у поверхности. Данное предположение подтверждается графиком и диаграммой соответственно (рис.3).

Рис. 3. График зависимости и диаграмма распределения напряженности поля

Как видно из графиков наибольшая напряженность достигается на поверхности катушки и наименьшая соответственно ближе к центру. Магнитожидкостный элемент способствует уменьшению продольной компоненты магнитного поля находящегося вокруг катушки.

Программный продукт является узкоспециализированным, за основу расчетов взят семисекционный электромагнитный генератор аппарата циркуляции биологических жидкостей. В данном программном продукте возможно проводить расчеты и осуществлять моделирование поля различных цилиндрических катушек.

Библиографический список

1. Корнилова Н. В. Постановка задачи разработки пространственно распределенного генератора электромагнитных полей для аппарата «Искусственное сердце» / Н. В. Корнилова // Современные технологии в машиностроении : сб. тр. XII Междунар. науч.-практ. конф. – Пенза: ПДЗ, 2008. С. 245–247.

2. Корнилова, Н. В. Электромагнитная управляющая оболочка для магнитожидкостных сенсоров аппарата «Искусственное сердце» / Н. В. Корнилова // Современные проблемы электрофизики и электродинамики жидкостей: сб. докл. Х Междунар. конф. – СПб.: СОЛО, 2012. С. 225–227.