К.т.н., Василенко В.С., Дубчак О.В.

Національний авіаційний університет(НАУ), Україна

ВИБІР ПАРАМЕТРІВ ЛИШКОВИХ КОДІВ ПРИ ЗАБЕЗПЕЧЕННІ ЦІЛІСНОСТІ ІНФОРМАЦІЙНИХ ОБ’ЄКТІВ

Вступ Розвиток інформаційних технологій вимагає гарантування захисту інформації, перш за все такої її властивості, як цілісність. Для вирішення задач забезпечення цілісності інформаційних об’єктів застосовується завадостійке чи завадостійке корегуюче кодування. Широкого використання в завадостійкому кодуванні набули системи лишкових класів (СЛК) в класичному вигляді чи у вигляді коду умовних лишків (ЛУ – коді). Відомо, що в цих системах кодова комбінація розглядається як деяке число. Для задач цього класу постає традиційна проблема розрізняння невикривлених кодових комбінацій (чисел, базових кодових слів (БКС)) від викривлених^[1]. Невикривленими вважаються такі числа, величина яких не перевищує наперед визначеного діапазону представлення невикривлених чисел - робочого діапазону , де – основи системи числення, обрані для даної системи представлення. Відомо, що в кодах для завадостійкого кодування вводиться надлишковість у вигляді реального чи умовного лишку від розподілу вихідного числа на контрольну основу (чи ). Її введення приводить до розширення діапазону представлення числа до величини . При цьому вважається, що невикривлені числа містяться у межах робочого діапазону , а викривлені числа зосереджені за межами робочого діапазону, тобто . При виборі чи визначенні елементів системи числення в СЛК важливо вибрати такі основи цієї системи, які б забезпечили у завадостійких кодах просте і надійне виявлення факту викривлення, а в корегуючих кодах – місце і величини можливих викривлень у БКС. При цьому основи, які створюють робочий діапазон, мають бути взаємно простими числами.

Вибір параметрів ЛУ кодів у задачах контролю цілісності Як згадувалось, викривлені числа задовольняють умові . Отже, для виявлення наявності викривлень досить визначити, в якому з діапазонів - робочому чи контрольному - знаходиться число, правильність якого перевіряється. Для цього слід вимагати, щоб викривлення символу початкового числа , тобто лишку, по будь-якій основі, наприклад, по основі , збільшувало б початкове невикривлене число () А = на величину , що забезпечує вихід викривленого числа в контрольний діапазон.

Тоді викривлене число перейде з початкового діапазону в контрольний діапазон (див. рис. 1), наприклад, в діапазон [, ) величиною . Таким чином буде забезпечена умова .

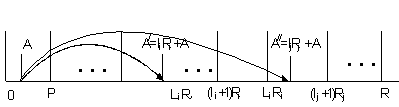
Рис. 1. До виходу викривленого числа за межі робочого діапазону

Звідси витікає , тобто, при найменшому значенні , . Отже, умовою однозначного визначення наявності викривлень є перевищення величиною контрольної основи величини будь-якої з інших основ. В останніх виразах: – величина викривлення;– значення невикривленого символу (лишку за основою з номером ); – номер інтервалу, в який потрапляє число, викривлене за основою з номером ; – величина даного інтервалу; – значення викривленого символу, – величина викривлення – го символу.

Вибір параметрів ЛУ кодів у задачах контролю та поновлення цілісності У задачах даного класу встановлення факту наявності порушення цілісності інформаційного об’єкту є недостатнім, необхідно визначити також місце викривлення та його величину. Для вирішення такої проблеми треба ідентифікувати викривлене число або величину викривлення з номером основи (), за якою таке викривлення має місце, та визначити величину цього викривлення (відповідно чи , де - номери основ у прикладі). Для цього можна використати той факт, що аналогічне викривлення за основою переводить викривлене число у діапазон [, ) величиною (див. рис. 1).

З наведеного витікає, що механізми визначення наявності, місця виникнення та величини викривлення повинні ґрунтуватися на виявленні тим чи іншим шляхом хоча б однієї з таких взаємно пов’язаних величин, як , , та, відповідно, , , , . З наведеного витікає також, що для ідентифікації викривленого числа чи величини викривлення з номером основи слід забезпечити попадання викривлених за різними основами чисел в різні діапазони. Це можливо за умови, що відстань між двома довільними діапазонами, в які можуть потрапити викривлені числа, перевищувала б максимальне значення невикривленого числа (). Наприклад, при (при зворотному співвідношенні результат не зміниться):

, чи . (1)

Звідси: ,

, , .

Оскільки значення контрольної основи, що обирається, повинно перевищувати величину, яка визначається дробовим числом, то максимального значення ця величина набуде при максимальному значенні чисельника та мінімальному значенні знаменника. Максимальне значення чисельника в цьому виразі дорівнює добутку двох найбільших з основ системи числення , а мінімальне значення знаменника, за умови його цілочисленості, .

Дорівнювати нулю знаменник може лише тоді, коли , що може бути досяжним лише при , а , що є неможливим. (Нагадаємо, що основи системи числення, наразі це величини , є взаємно простими числами). Отже, в разі визначення величини та місця викривлення за фактом попадання викривленого числа до інтервалу , вимога до величини контрольної основи може бути записаною у вигляді:

. (2)

Один з відомих механізмів, що реалізує так званий z – алгоритм^[1], саме використовує той факт, що оскільки величина первинного числа завжди є величиною меншою, ніж (тобто ), то й відстань між викривленим числом і лівою межею діапазону, в який це викривлене число потрапило, також є величиною меншою ніж . Наприклад, для випадків, відображених на рис.1:

. (3)

Оскільки в системах нерівностей (3) справедливими є тільки нерівність для однієї основи , а отже і для одного значення (де – номер інтервалу, в який потрапляє число, викривлене за цією основою з номером), то цей факт дозволяє однозначно визначити і місце, і величину викривлення та здійснити корегування викривлення.

Інший з механізмів^[2] - механізм на основі так званої нулізації - використовує факт переходу викривленого числа з початкового діапазону в деякий інший діапазон, величиною , наприклад, в діапазон , чи в діапазон ,. Цей механізм шляхом визначення так званого мінімального числа , наприклад для випадків, представлених на рис. 2, величиною чи , дозволяє визначити ліву межу діапазону чи і здійснити корегування визначеного викривлення^[3].

Рис. 2. До виходу викривленого числа за межі робочого діапазону

Цікаво визначити можливість виконання умови, щоб число з будь-якими викривленнями, що можуть виникнути в лишках за одною з довільних основ величиною , завжди відрізнялося від значення, яке має ліва межа інтервалу, наприклад (де ). Зрозуміло, що для цього слід забезпечити виконання наступного виразу: . (4)

З виразу (4) витікають дві нерівності. Перша із них при < має вигляд:

.

Звідси: , , .

Як і раніше, при максимальному значенні чисельника, яке досягається при , і мінімальному значенні знаменника , отримаємо , що є неможливим.

Друга з нерівностей при > має вигляд . Перетворення цієї нерівності приводить до виразу , що також є неможливим.

З останнього аналізу випливає висновок про неможливість забезпечення умови, щоб число з будь-якими викривленнями, що можуть виникнути в лишках за одною з довільних основ величиною , завжди відрізнялося від значення лівої межі цього інтервалу. Отже, викривлення за будь-якою з основ завжди переводить викривлене число в один з контрольних піддіапазонів з деяким номером, наприклад, з номером k; різниця між викривленим й обома межами інтервалу є меншою за величину цього інтервалу , а отже є меншою ніж максимальне значення невикривленого числа .

Отже, що в разі попадання викривлення величиною в діапазон викривлене число, величина якого , може залишитися в цьому ж діапазоні, чи викривлене число таке, що , може потрапити в інший діапазон .

Висновки З урахуванням вищевикладеного зрозуміло, що, в разі дотримання вимог щодо величин викривлень за різними основами у вигляді (1) та щодо величини контрольної основи у вигляді (2), можливим є випадок, коли нулізація при наявності викривлень за різними основами дасть однакове значення номеру піддіапазону. Це, в свою чергу, показує при таких значеннях контрольної основи можливість неоднозначного тлумачення результатів нулізації і необхідність додаткових перевірок.

Для виключення подібних випадків неправильного визначення місця і, відповідно, і величин викривлень, слід підсилити вимоги (1) та (2) щодо величини контрольної основи та записати їх у вигляді

, (5)

. (6)

Таким чином, при дотриманні умов (5), (6) результат нулізації у вигляді номеру піддіапазону має однозначний функціональний зв’язок з величиною викривлення , що дає також можливість однозначного визначення місця і величини викривлення, тобто визначення величин та , а отже, і величини власне викривлення .

Література:

1. Василенко В.С. Использование ВУ - кодов для повышения верности информации в радиоканалах // Матеріали 28 НТС Асоціації зв’язку України. – К.: КВІРТУ ППО. – 1991. – С. 23

2. Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах // М.: Сов. Радио.- 1966. – 421 с.

3. Василенко В.С., Матов О.Я. Узагальнені завадостійкі коди в задачах забезпечення цілісності інформаційних об’єктів. Код умовних лишків// К.: Реєстрація, зберігання і обробка даних. - 2006. - том 6, № 4. -С.82.