Делей В.И., Ленюк М.П.

Чернівецький факультет НТУ “Харківський політехнічний інститут”

СУММИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ ПО СОБСТВЕННЫМ ЭЕЛЕМЕНТАМ ГИБРИДНОГО ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА ЭЙЛЕРА-БЕССЕЛЯ НА СЕГМЕНТЕ [R₀, R₂] ПОЛЯРНОЙ ОСИ

Методом сравнения решений краевой задачи на сегменте [R₀, R₂] полярной оси с точкой сопряжения r = R₁ Î (R₀, R₂) для сепаратной системы из дифференциальных уравнений Эйлера и Бесселя, построенного, с одной стороны, методом функций Коши, а, с другой стороны – методом конечного гибридного интегрального преобразования Эйлера-Бесселя просуммирована полипараметрическая семья функциональных рядов со собственным элементам гибридного дифференциального оператора Эйлера-Бесселя.

Рассмотрим задачу построения ограниченного на множестве I₁ = {r : r Î [R₀, R₁) (R₁, R₂); 0 < R₀ < R₁ < R₂ < ¥} решения сепаратной системы дифференциальных уравнений Эйлера и Бесселя

, r Î (R₀, R₁),

, r Î (R₁, R₂) (1)

по краевым условиям

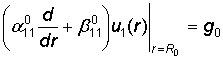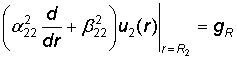, (2)

и условиям сопряжения

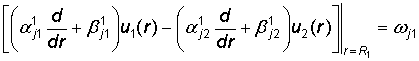, j = 1, 2. (3)

В равенствах (1) принимают участие дифференциальные операторы:

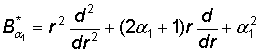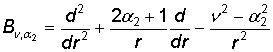, , 2a_j+1 > 0,

– дифференциальный оператор Эйлера [1], – дифференциальный оператор Бесселя [2], n ³ a₂ > –1/2.

Мы предполагаем, что выполнены условия на коэффициенты: £ 0, ³ 0, ³ 0, ³ 0, || + ¹ 0, ¹ 0, c₁₁c₂₁ > 0, , j = 1, 2.

Фундаментальную систему решений для дифференциального уравнения Эйлера ( – )v = 0 образуют функции v₁ = и v₂ = [1]; фундаментальную систему решений для дифференциального уравнения Бесселя (B_{n, a} – q²)v = 0 образуют функции v₁ = I_{n, a}(qr) и v₂ = K_{n, a}(qr) [2].

Наличие фундаментальной системы решений позволяет построить общее решение краевой задачи (1) – (3) методом функций Коши [1, 3]:

u₁(r) = A₁ + B₁ + ,

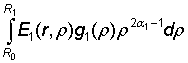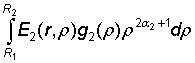u₂(r) = A₂ + B₂ + , (4)

где E_j(r, r) – функции Коши [1, 3]:

,

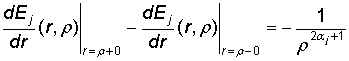, j = 1, 2. (5)

Введем в рассмотрение функции:

,

,

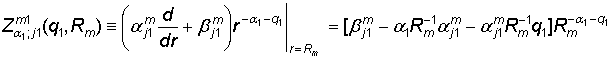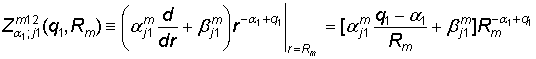, j = 1, 2,

.

Непосредственно проверяется, что функция Коши

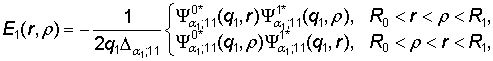(6)

Определим функции

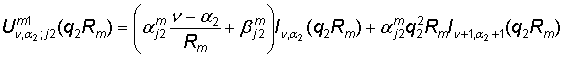, j 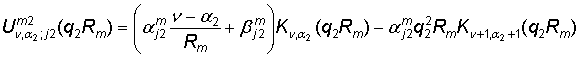= 1, 2,

,

, m=1, 2,

.

Непосредственно проверяется, что функция Коши

´

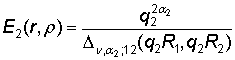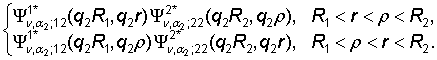´ (7)

Обратимся к формулам (4). Краевые условия (1) и условия сопряжения (3) для определения величин A_j и B_j (j = 1, 2) дают неоднородную алгебраическую систему из четырех уравнений:

,

,

,

. (8)

Здесь принимает участие функция

G₁₂ = –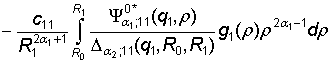

– .

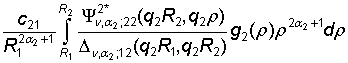Предположим, что выполнено условие однозначной разрешимости краевой задачи (1) – (3): для (a) = (a₁, a₂) и любого ненулевого вектора = {q₁; q₂} ¹ определитель алгебраической системы (8)

–

– ¹ 0. (9)

Определим главные решения краевой задачи (1) – (3):

1) порожденные краевым условием в точке r = R₀ функции Грина

–

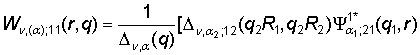– ], (10)

;

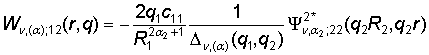2) порожденные краевым условием в точке r = R₂ функции Грина

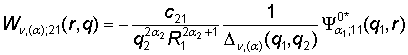, (11)

–

– ];

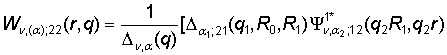3) порожденные неоднородностью условий сопряжения функции Грина

, ,

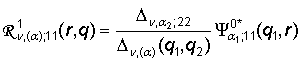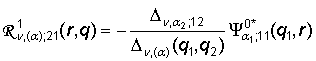(12)

, ;

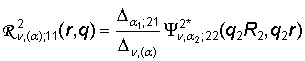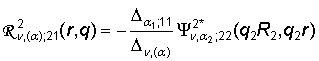4) порожденные неоднородностью системы (1) функции влияния

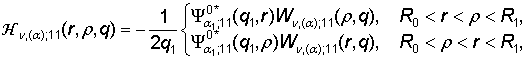(13)

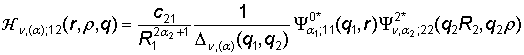, q = (q₁, q₂), ,

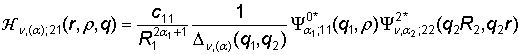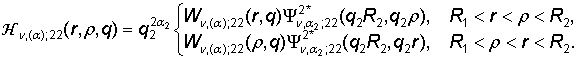
В результате однозначной разрешимости алгебраической системы (8) в силу условия (9) и подстановки вычисленных величин A_j, B_j (j = 1, 2) в формулы (4) имеем единственное решение краевой задачи (1) – (3):

u_j(r) = + + + +

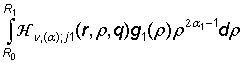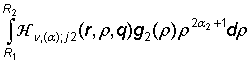+ + , j = 1, 2. (14)

Построим теперь решение краевой задачи (1) – (3) методом интегрального преобразования, порожденного на множестве I₁ гибридным дифференциальным оператором (ГДО)

M_{n, (a)} = q(r – R₀)q(R₁ – r) + q(r – R₁)q(R₂ – r). (15)

Так как ГДО самосопряженный и на множестве I₁ не имеет особых точек, то его спектр действительный и дискретный [5]. Ему отвечает дискретная вектор-функция.

Определение. Областью определения ГДО M_{n, (a)} назовем множество G вектор-функций g(r) = {g₁(r); g₂(r)} с такими свойствами: 1) вектор-функция f(r) = {[g₁(r)]; [g₂(r)]} непрерывная на множестве I₁; 2) функции g_j(r) удовлетворяют условиям сопряжений

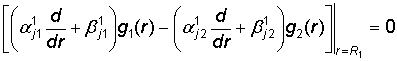, j = 1, 2; (16)

3) функции g_j(r) удовлетворяют краевым условиям

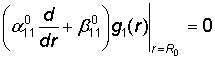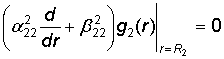, . (17)

Собственные элементы (спектр и отвечающую ему спектральную функцию) ГДО M_{n, (a)} найдем как ненулевое решение системы уравнений

, r Î (R₀, R₁),

, r Î (R₁, R₂) (18)

по однородным условиям сопряжения (16) и однородным краевым условиям (17), считая, что функция V_{n, (a)}(r, b) = { V_{n, (a); 1}(r, b); V_{n, (a); 2}(r, b)} Î G; b_j = b_j(b) = ()^1/2, ³ 0, j = 1, 2. Здесь b – спектральный параметр.

Фундаментальную систему решений для дифференциального уравнения Эйлера ( + b²)v = 0 образуют функции v₁ = r ^–acos(b lnr) и v₂ = r ^–asin(b lnr) [1]. Фундаментальную систему решений для дифференциального уравнения Бесселя (B_{n, a} + b²)v = 0 образуют функции v₁ = J_{n, a}(br) и v₂ = N_{n, a}(br) [2].

Положим

V_{n, (a); 1} (r, b) = A₁cos(b₁lnr) + B₁sin(b₁lnr),

V _{n, (a); 2}(r, b) = A₂(b₂r) + B₂(b₂r). (19)

Условия сопряжения (16) и краевые условия (17) для определения величин A_j, B_j (j = 1, 2) дают однородную алгебраическую систему из четырех уравнений:

= 0,

= 0, j = 1, 2,

= 0. (20)

В равенствах (20) принимают участие функции:

= – ,

= + ,

,

.

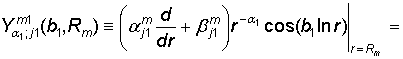
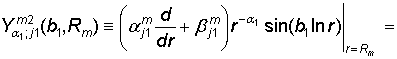
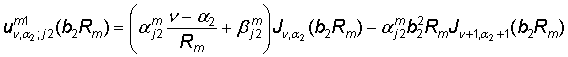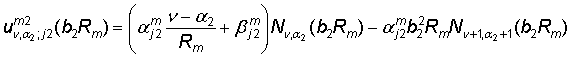Алгебраическая система (20) имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю [4]:

d_{n, (a)}(b) º = 0. (21)

Здесь принимают участие функции:

= , j = 1, 2,

=.

Корни b_n трансцендентного уравнения (21), будучи собственными числами ГДО M_{n, (a)}, составляют дискретный спектр [5]: действительные, простые, симметричные относительно b = 0 и образуют на полуоси b > 0 монотонно возрастающую последовательность с единственной предельной точкой b = ¥.

Подставим b = b_n в систему (20) и отбросим последнее уравнение в силу линейной зависимости. Предположим, что A₁ = A₀,
B₁ = –A₀, где A₀ подлежит определению, ,
j = 1, 2. Тогда для определения A₂, B₂ получаем алгебраическую систему:

, j = 1, 2.

Отсюда при A₀ = находим, что

A₂ = –w_{n, (a); 2}(b_n), B₂ = w_{n, (a); 1}(b_n),

w_{n, (a); j}(b_n) = , j = 1, 2.

Подставив в равенства (19) вычисленные значения A_j, B_j имеем компоненты спектральной вектор-функции V_{n, (a)}(r, b_n):

[ –

– ],

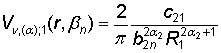. (22)

Следовательно, спектральному спектру отвечает спектральная функция .

Согласно с работой [5] имеем утверждения.

Теорема 1. Система собственных функций ГДО
M_{n, (a)} ортогональная на множестве I₁ с весовой функцией

s(r) = q(r – R₀)q(R₁ – r)s₁ + q(r – R₁)q(R₂ – r) s₂ ,

где , s₂ = 1, полная и замкнутая. При этом квадрат нормы собственной функции вычисляется по правилу:

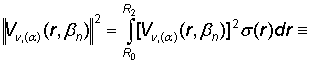
º 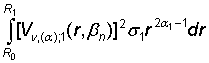+ 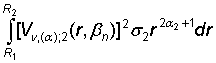. (23)

Теорема 2. Любая функция g(r) Î G представляется абсолютно и равномерно сходящимся на множестве I₁ рядом Фурье по системе :

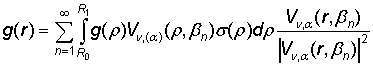. (24)

Ряд Фурье (24) определяет прямое H_{n, (a)} и обратное конечное гибридное интегральное преобразование, порожденное на множестве I₁ ГДО M_{n, (a)}:

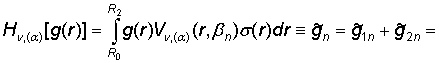
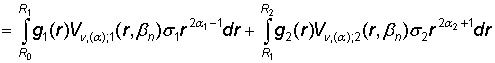, (25)

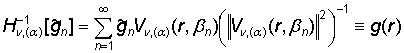. (26)

Теорема 3. Если вектор-функция g(r) Î G, удовлетворяет условиям сопряжения (3) и краевым условиям (2), то имеет место основное тождество интегрального преобразования ГДО M_{n, (a)}:

– +

+ + ,

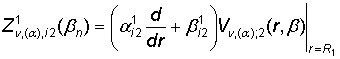, i = 1, 2. (27) Запишем систему (1) в матричной форме:

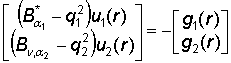. (28)

Интегральный оператор H_{n, (a)} согласно правила (25) представим в виде операторной матрицы-строки:

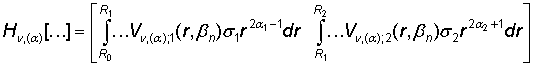. (29)

Применим по правилу умножения матриц операторную матрицу-строку (29) к системе (28). В силу тождества (27) получаем уравнение:

= +

+ +

+ . (30)

Мы предполагали, что max{; } = . В этому случае = 0, ³ 0 (b_1n = b_n, b_2n = ()^1/2). Если бы max{; } = , то мы имели бы: ³ 0, = 0 (b_1n = ()^1/2, b_2n = b_n). В равенстве (30) вместо () было бы ().

Из уравнения (30) получаем функцию

+ +

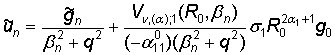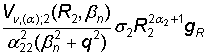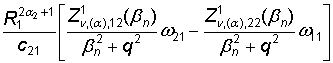+ , q² = max{; }. (31)

Оператор согласно правила (26) как обратный к (29) представим в виде операторной матрицы-столбца:

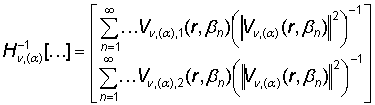. (32)

Применяя по правилу умножения матриц операторную матрицу-столбец (32) к матрице-элементу [], где функция определена по формуле (31), имеем единственное решение краевой задачи (1) – (3):

u_j(r) = =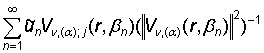

= +

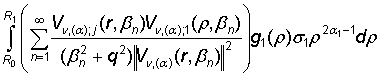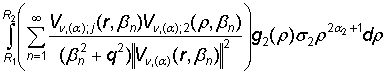+ + (33)

+ +

+ +

+ –

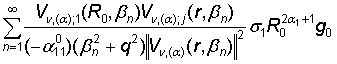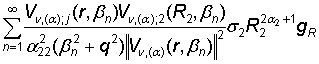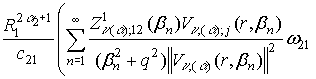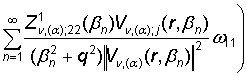– , j = 1, 2.

Сравнивая решения (14) и (33) в силу единственности, получаем формулы суммирования полипараметрических функциональных рядов по собственным элементам ГДО M_{n, (a)}:

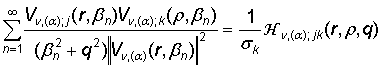, j, k = 1, 2, (34)

, j = 1, 2, (35)

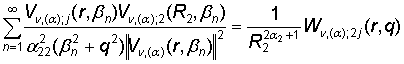, j = 1, 2, (36)

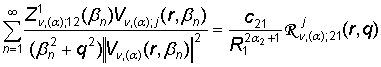, j = 1, 2, (37)

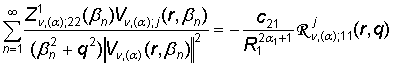, j = 1, 2. (38)

Функции влияния определены по формулам (13), функции Грина – по формулам (10), функции Грина – по формулам (11) и функции Грина – по формулам (12). Так как эти главные решения не зависят от неравенства () ³ 0 или от неравенства () ³ 0, то можно положить > 0, суживая при этом семью функциональных рядов.

Итогом изложенного выше есть утверждение.

Теорема. Пусть компоненты g_j(r) функции g(r) Î G удовлетворяют краевым условиям (2) и условиям сопряжения (3). Если при этом выполняется условие (9) однозначной разрешимости краевой задачи (1) – (3), то имеют место формулы (34) – (38) суммирования полипараметрических функциональных рядов по собственным элементам ГДО M_{n, (a)}, определенного равенством (15).

ЛИТЕРАТУРА

1. Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.

2. Ленюк М.П. Исследование основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев, 1982. – 62 с. – (Препринт / АН УССР. Ин-т математики; 83.3).

3. Шилов Г.Е. Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328 с.

4. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1971. – 432 с.

5. Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні інтегральні перетворення, породжені диференціальними рівняннями другого порядку. – Чернівці: Прут, 2001. – 228 с.