Современные информационные технологии/3. Программное обеспечение

К.ф.-м.н. Любанова А.Ш., Кузнецов В.А.

Сибирский Федеральный Университет, Россия

ОПТИМИЗАЦИЯ ГРАНУЛОМЕТРИЧЕСКОГО СОСТАВА ПОРОШКОВЫХ СМЕСЕЙ

Данная работа посвящена вопросам применения статистических методов моделирования для решения задач оптимальной упаковки гранулированных смесей. Такие задачи актуальны в порошковой металлургии и производстве композитных материалов.

Порошковая металлургия позволяет не только экономить металл, существенно снижать трудоёмкость изготовления деталей, себестоимость продукции, но и создавать композиционные материалы с уникальным сочетанием свойств. Структурные особенности ультрадисперсного сочетания материалов дают возможность получать рекордные значения твёрдости и прочности материалов, переносить воздействия циклических колебаний температуры, напряжения и влияние других сильно действующих факторов. Соответствующая технология позволяет получать однородные системы из составляющих, нерастворимых друг в друге или имеющих очень различные точки плавления материалов с регулируемой пористостью и т.д.

Технология получения заготовок для дальнейшего производства деталей из порошковых материалов включает три основных стадии: а) смешение порошков в некоторых пропорциях; б) обработка порошковой массы давлением (холодное или горячее прессование); в) спекание порошковых брикетов. Основной недостаток технологии в целом – недостаточная прочность порошковых изделий – связан с наличием остаточных пор. Борьбу с остаточной пористостью можно вести на всех стадиях технологического процесса, и с этим связаны различные задачи математического моделирования.

В настоящее время не существует строгой физической теории диспергированных твёрдых фаз, и тем самым состояние порошковых смесей на первой и в начале второй стадии процесса не может быть описано с помощью каких-либо динамических уравнений. С другой стороны, завершающая обработка давлением и спекание порошковых брикетов по самой целевой постановке связана с уменьшением объёма пор в достаточно сложных физических процессах, а тем самым с динамическим изменением физических параметров материала. Всё это затрудняет адекватное математическое моделирование процессов порошковой металлургии.

В этой связи соответствующие процессы естественно рассматривать в рамках моделей, использующих некоторые осреднённые физические характеристики для тех материалов и тех этапов различных стадий технологии, когда такие характеристики известны из прямого физического эксперимента или могут быть рассчитаны по его данным.

Одним из способов повышения эффективности технологического процесса в целом является уменьшение пористости на первой стадии при изготовлении порошковых смесей.

Если в первом приближении не учитывать физические факторы, то плотность укладки гранул зависит, вообще говоря, от трёх геометрических факторов: формы частиц; их размеров; взаимного расположения в резервуаре.

В некоторых технологиях изготовления порошков форма гранул близка к сферической. Этим характеризуются, например, бронзовые и железные порошки, получаемые распылением. Если к тому же предположить, что гранулы могут располагаться (например, под воздействием вибраций) наиболее плотно, то остаётся единственный управляющий фактор – размеры частиц. Соответственно можно рассматривать задачу о зависимости пористости брикета от пропорции, в которых смешиваются частицы различных размеров.

Целью данного исследования является построение математической модели максимально плотной упаковки шаровидных гранул случайного размера и разработка статистического алгоритма компьютерного моделирования такой упаковки.

В работах [2, 4] сделана попытка приближенно решить эту задачу на основе геометрического анализа ячейки смеси, состоящей из нескольких соприкасающихся шаров. В работе [2] показано, что если все шары имеют одинаковые размеры, то наименьшая пористость получается при так называемой гранецентрированной их упаковке; такая упаковка характеризуется тем, что в каждой ячейке пространства центры шаров совпадают с вершинами тетраэдра.

При чисто геометрическом подходе, использованном в упомянутых работах, предметом изучения являются различные возможности равномерного в пространстве взаимного расположения («упаковки») частиц сферической формы и расчёт получающейся в каждом случае пористости. Ввиду равномерности гипотетического распределения частиц задача сводится к расчёту отдельной ячейки симметричной структуры.

Анализ упомянутых работ приводит к заключению, что в основу расчёта ячейки могут быть положены два различных принципа: естественный принцип взаимного касания частиц различных размеров и принцип свободной фильтрации частиц меньших размеров между частицами больших размеров.

Согласно первому принципу частицы меньшего радиуса вписываются в свободное пространство между частицами большего радиуса, образующими правильную периодическую структуру попарно касающихся шаров. В оставшееся свободное пространство между частицами двух указанных радиусов вписываются частицы ещё меньшего радиуса и т.д., каждый раз с соблюдением условий касания с возможно большим числом соседей. Радиусы частиц такой неоднородной смеси образуют убывающую последовательность значений [3, 4]. Поэтому подбор на основе геометрического «принципа касаний» представляется практически малоэффективным для повышения плотности упаковки.

Соблюдение принципа свободной фильтрации частиц меньших размеров между частицами больших размеров предполагает, что частицы меньшего радиуса могут свободно проникать в поры между частицами более крупными. Это означает, что ещё более мелкие частицы очередной группы фракции должны иметь (в рамках той же геометрической модели) радиус существенно меньший, чем радиус частиц предыдущей фракции. Смесь, получаемую на основе этого принципа, естественно назвать многофракционной.

При свободной фильтрации соблюдение жёстких требований к реальному размеру частиц очередной фракции не столь существенно, как в предшествующем случае. Не слишком важны и предположения относительно формы частиц, поскольку эффект достигается в основном за счёт резкого разрыва в размерах частиц фракций. Таким образом, принцип свободной фильтрации оказывается эффективнее принципа взаимного касания.

В [1] впервые предложен строгий математический анализ проблемы оптимизации гранулометрического состава порошковых смесей. Результаты математического эксперимента, проведённого методом Монте-Карло, получены в рамках сотрудничества МГУ и ПО ЗИЛ.

Не будем интересоваться конкретным геометрическим расположением частиц (гранул) в некотором сосуде, ибо, не предполагая периодичности структуры, рассчитать такое расположение практически невозможно при большом числе частиц. Будем использовать лишь общие факты, вытекающие из рассмотрения возможных положений гранул. Такой подход при последовательном математическом анализе даёт возможность получить заранее неочевидные ответы на вопросы, связанные с математической постановкой задачи о подборе гранулометрического состава.

Назовём частицу звёздной, если внутри неё есть точка, «центр звёздности», обладающая следующим свойством: любой луч с началом в этой точке пересекает границу частицы лишь однажды. Простейшей звездной частицей является шар.

Все частицы, образующие смесь, будем считать шарами. Такое упрощение оправдано настолько малыми размерами реальных частиц по сравнению с габаритами заполняемой емкости, что отклонением их формы от шаровидной можно пренебречь.

Под линейным размером такой частицы будем понимать ее диаметр. Любой гранулометрический состав, помещённый в заданный объём Q, можно охарактеризовать набором диаметров частиц {d_i}, число которых N может быть весьма большим. Такому набору можно поставить в соответствие функцию распределения

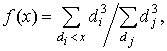
называемую объёмной гранулометрией. Поскольку при принятых предположениях объём, занимаемый частицей, , то f(x) с точностью до коэффициента выражает относительный объём, заполненный частицами, диаметр которых не превосходит x. Поэтому зная f(x), можно указать, в частности, в каких массовых пропорциях при этом смешаны частицы, обладающие теми или другими диаметрами.

Будем говорить, что набор частиц {d_i} плотно упаковывается в некоторую форму Q, если возможно такое его размещение внутри Q, что, с одной стороны, частицы не будут пересекаться между собой и, с другой стороны, для любого μ>1 набор частиц {μd_i} уже не может быть размещён без взаимного пересечения каких-либо частиц.

Пусть Q – форма такого брикета, который является плотной упаковкой частиц, соответствующих распределению по размерам f(x). Объём всех N частиц в брикете Если V_Q есть видимый объём пористого брикета (V_Q = const), то пористость такой упаковки ξ_N = 1–(V_N/V_Q). Оказывается [1], что существует , не зависящий от формы Q пористого брикета. Очевидно, что указанный предел является функционалом от f, т. е. ξ = ξ[f]. Этот функционал назовём функционалом пористости плотной упаковки частиц состава f(x).

На практике имеем дело с порошками, размеры частиц которых заключены в пределах d_m ≤ d ≤ d_M. В этом случае задача оптимизации гранулометрического состава формулируется так: найти f(x) на множестве функций распределения F* = {f: f(d_m) = 0, f(d_m + 0) = 1}, которая доставляет минимум функционалу x.

Для решения поставленной задачи оптимизации в данной работе предлагается метод расчёта значений целевого функционала, который является модификацией метода стохастических испытаний [1]. Принципиальную схему метода кратко опишем применительно к гексагональной периодической структуре. В этом случае V_i = (4/3)πr³_i, где r_i = d_i/2. В качестве основы структуры возьмем неправильный тетраэдр, вершины которого совпадают с центрами попарно касающихся шаров радиусов r_i1, r_i2, r_i3, r_i4. Очевидно, если известны четыре таких числа, то можно вычислить объём тетраэдра, суммарный объём тех частей шаров, которые находятся внутри тетраэдра.

Алгоритм вычисления приближения к функционалу пористости ξ = ξ [f] основан на процедуре формирования на ЭВМ порошковой смеси с соблюдением пропорций, диктуемых функцией f(x). Формирование производится последовательным образованием одной элементарной ячейки за другой, пока не будет заполнен столь большой объём, что по нему можно судить о величине плотности его структуры.

Для того чтобы не нарушить пропорции при формировании отдельной ячейки, примем f(x) за интегральную вероятностную функцию распределения частиц по размерам:

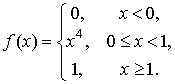
Соответственно величины r_i радиусов частиц будем рассматривать как случайные величины, распределённые по указанному закону.

Для формирования первой ячейки нужно выбрать четыре случайных числа: r₁, r₂, r₃, r₄. Эти значения определяются как решения уравнения

f(x) = γ_n, n = 1, 2, 3,…, (1)

где γ_n – случайная величина с равномерным распределением на отрезке [0, 1], задаваемая программой-датчиком, входящим в состав математического обеспечения ЭВМ. Поскольку x Î [0, 1], при каждом γ_n решение уравнения (1) имеет вид: .

При n =1 радиусы всех шаров одинаковы и равны , i = 1, 2, 3, 4. К полученной первой ячейке пристраиваются последующие по схеме, представленной на рисунке 1.

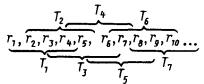
Рисунок 1. Схема выборки радиусов шаров при расчете плотности упаковки методом Монте-Карло

Для этого каждый раз выбирается новое случайное число γ_n и решается уравнение (1). Параллельно с образованием нового n-го тетраэдра накапливаются суммы и , где s_1n – суммарный объем частей шаров внутри тетраэдров, s_2n – суммарный объём тетраэдров. Затем вычисляется величина ξ = 1 – σ_1n/σ_2n, характеризующая приближенно среднюю плотность в структуре из n элементарных ячеек. Одновременно вычисляется величина |ξ_n – ξ_n-1|, (ξ₀ = 0), которая сравнивается с заданной константой ε₁, если |ξ_n–ξ_n-1| > ε₁, то к некоторому счётчику N добавляется единица, в противном случае этого не делается. Таким образом, находится число случаев N, когда два соседних приближения величины ξ недостаточно близки. Поскольку число испытаний n также известно, попутно считается соотношение N/n, аппроксимирующее вероятность того, что соседние приближения недостаточно близки. Процесс заканчивается по условию N/n < ε₂, где ε₂ – также заданная величина.

Число гранул в реальных смесях очень велико, а их радиусы случайны. Поэтому вместо точных значений s_1n и s_2n удобнее использовать их статистические оценки и , где – объем четырех частей среднестатистических шаров радиуса , заключенных в правильный тетраэдр объема .

Литература:

1. Крискин Ю. А. О пористости плотноупакованного порошка из сферических частиц // Докл. АН СССР. – 1982. – Т. 265. – №4. – С. 798-801.

2. Макклинток Ф., Аргон А. Деформация и разрушение металлов. М.: Мир, 1970. 443 с.

3. Hildebrand J. H., Morrel М. E. The distribution of molecules in a model liquid // Chemical Physics. 1936. V. 4. P. 224-228.

4. Levin М. М., Chernick J. A numerical model of random packing of spheres//Nature. 1965. V. 208, N. 5005. P. 68-69.