Математика/1.Дифференциальные
и интегральные уравнения
К.ф.-м.н. Мартинюк О. В.
Чернівецький
національний університет імені Юрія Федьковича,Україна
Задача Коші для сингулярних еволюційних рівнянь нескінченного
порядку
При розв’язуванні задач математичної фізики, квантової механіки, теорії
теплопровідності, тепломасопереносу, кристалографії, задач про взаємодію тіл,
при математичному моделюванні різних реальних процесів виникає необхідність
дослідження крайових задач (зокрема, задачі Коші) для диференціальних рівнянь
(та систем рівнянь) з різними особливостями та виродженнями, коли, наприклад,
рівняння має особливості в коефіцієнтах, вироджується тип рівняння, рівняння
замість диференціальних операторів містять псевдодиференціальні оператори, у
рівняннях наявні випадкові збурення і т.п.
Багато таких задач мають природну постановку і у різних просторах
узагальнених функцій, оскільки досить часто крайові умови мають особливості в
деяких точках межі або ділянках межі. Такі функції допускають регуляризацію у просторах
узагальнених функцій скінченного порядку (типу розподілів Соболєва-Шварца), або
їх можна трактувати як узагальнені функції нескінченного порядку (типу
ультрарозподілів, гіперфункцій), якщо порядок особливостей вищий за степеневий.
До рівнянь, які мають особливості в коефіцієнтах, відносяться ![]() -параболічні рівняння – рівняння з оператором Бесселя
-параболічні рівняння – рівняння з оператором Бесселя ![]()
![]() , який вироджується за просторовою змінною, а саме рівняння
при цьому вироджується на межі області.
, який вироджується за просторовою змінною, а саме рівняння
при цьому вироджується на межі області. ![]() -параболічні рівняння за своїми внутрішніми властивостям
близькі до рівномірно параболічних рівнянь.
-параболічні рівняння за своїми внутрішніми властивостям
близькі до рівномірно параболічних рівнянь.
Теорія класичних розвязків задачі Коші для таких рівнянь побудована у
працях М. І. Матійчука, В. В. Крехівського, С. Д. Івасишена і В. П. Лавренчука
[1,2] та ін. Задача Коші для сингулярних параболічних рівнянь у класах
розподілів та у класах узагальнених функцій типу S' вивчалась Я. І. Житомирським, В. В. Городецьким, І. В. Житарюком,
В. П. Лавренчуком [3-5] та ін. Природним узагальненням сингулярних параболічних
рівнянь є сингулярні еволюційні рівняння нескінченного порядку, тобто
еволюційні рівняння з оператором Бесселя нескінченного порядку вигляду ![]() . У цій праці розвивається теорія задачі Коші для вказаних
рівнянь у більш широких, порівняно з просторами типу S' класах узагальнених початкових функцій нескінченного порядку, а
саме, в просторах типу W' аналітичних
функціоналів (озн. просторів типу S, S' див. в [6]).
. У цій праці розвивається теорія задачі Коші для вказаних
рівнянь у більш широких, порівняно з просторами типу S' класах узагальнених початкових функцій нескінченного порядку, а
саме, в просторах типу W' аналітичних
функціоналів (озн. просторів типу S, S' див. в [6]).
Наведемо основні означення, що стосуються топологічної структури
просторів типу W. Нехай M, ![]() – диференційовні,
парні на
– диференційовні,
парні на ![]() функції, зростаючі та опуклі на
функції, зростаючі та опуклі на ![]() , причому
, причому ![]() ,
, ![]() . За допомогою функцій M
тa
. За допомогою функцій M
тa ![]() Б. М. Гуревич [7]
ввів простори
Б. М. Гуревич [7]
ввів простори ![]() ,
, ![]() ,
, ![]() , названі ним просторами типу W. Зокрема, символом
, названі ним просторами типу W. Зокрема, символом ![]() позначається
сукупність цілих функцій
позначається
сукупність цілих функцій ![]() , для яких
, для яких ![]() (сталі
(сталі ![]() залежать лише від
функції
залежать лише від
функції ![]() ).
).
У ![]() вводиться топологія
індуктивної границі просторів
вводиться топологія
індуктивної границі просторів ![]() , де
, де ![]() складається з тих
функцій
складається з тих
функцій ![]() , для яких правильні нерівності
, для яких правильні нерівності
![]() ,
,
де ![]() – довільна додатна стала, менша за
– довільна додатна стала, менша за ![]() ,
, ![]() – довільна стала, більша за
– довільна стала, більша за ![]() . Якщо для
. Якщо для ![]() покласти
покласти
![]()
де ![]() , то з цими нормами
, то з цими нормами ![]() перетворюється в
досконалий зліченно-нормований простір.
перетворюється в
досконалий зліченно-нормований простір.
Символом ![]() позначатимемо
сукупність усіх цілих парних функцій з простору
позначатимемо
сукупність усіх цілих парних функцій з простору ![]() . Цей простір з відповідною топологією називатимемо основним
простором або простором типу
. Цей простір з відповідною топологією називатимемо основним
простором або простором типу ![]() , а його елементи – основними функціями. Сукупність функцій,
заданих на
, а його елементи – основними функціями. Сукупність функцій,
заданих на ![]() , які
допускають аналітичне продовження у всю комплексну площину і як функції
комплексної змінної є елементами простору
, які
допускають аналітичне продовження у всю комплексну площину і як функції
комплексної змінної є елементами простору ![]() , позначатимемо символом
, позначатимемо символом ![]() .
.
Нехай ![]() – деяка ціла парна
функція. Говоритимемо, що в просторі
– деяка ціла парна
функція. Говоритимемо, що в просторі ![]() задано оператор
Бесселя нескінченного порядку
задано оператор
Бесселя нескінченного порядку ![]() , якщо для довільної основної функції
, якщо для довільної основної функції ![]() ряд
ряд ![]() зображає деяку
основну функцію з простору
зображає деяку
основну функцію з простору ![]() .
.
Теорема 1. Нехай ![]() та
та ![]() – функції, двоїсті за Юнгом до функцій M та
– функції, двоїсті за Юнгом до функцій M та ![]() відповідно. Для того, щоб оператор Бесселя нескінченного порядку
відповідно. Для того, щоб оператор Бесселя нескінченного порядку ![]() був визначеним і неперервним у просторі
був визначеним і неперервним у просторі ![]() , необхідно й досить,
щоб ціла парна функція
, необхідно й досить,
щоб ціла парна функція ![]() була мультиплікатором у просторі
була мультиплікатором у просторі ![]() , тобто
, тобто
![]() .
.
Наслідок 1. Нехай ![]() – звуження оператора
– звуження оператора ![]() на
на ![]() . Тоді для довільної функції
. Тоді для довільної функції ![]() правильна рівність
правильна рівність
![]()
![]() ,
,
де ![]() та
та ![]() – пряме та обернене
перетворення Бесселя:
– пряме та обернене
перетворення Бесселя:
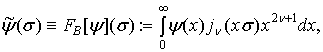
![]() ,
, 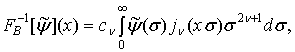
![]() – нормована функція Бесселя,
– нормована функція Бесселя, ![]() – фіксований
параметр,
– фіксований
параметр, ![]() – гамма-функція.
– гамма-функція.
Отже, ![]() можна розуміти як
псевдодиференціальних оператор, побудований за аналітичним символом
можна розуміти як
псевдодиференціальних оператор, побудований за аналітичним символом ![]() . Символом
. Символом 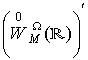 позначатимемо простір
усіх лінійних неперервних функціоналів над відповідним простором основних
функцій зі слабкою збіжністю, а його елементи називатимемо узагальненими
функціями.
позначатимемо простір
усіх лінійних неперервних функціоналів над відповідним простором основних
функцій зі слабкою збіжністю, а його елементи називатимемо узагальненими
функціями.
Розглянемо еволюційне рівняння
![]() (1)
(1)
де ![]() – оператор Бесселя
нескінченного порядку, побудований за функцією
– оператор Бесселя
нескінченного порядку, побудований за функцією ![]() у припущенні, що
у припущенні, що ![]() – мультиплікатор у
просторі
– мультиплікатор у
просторі ![]() і
і ![]() . Під розв’язком рівняння (1) розуміємо функцію
. Під розв’язком рівняння (1) розуміємо функцію 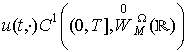 , яка задовольняє (1).
, яка задовольняє (1).
Функція ![]() є фундаментальним
розв’язком рівняння (1). Основні властивості функції G містяться в наступних твердженнях.
є фундаментальним
розв’язком рівняння (1). Основні властивості функції G містяться в наступних твердженнях.
Лема 1. ![]()
![]() при кожному фіксованому
при кожному фіксованому ![]() ;
;
![]()
![]() ,
, ![]()
![]() .
.
Лема 2. Функція ![]() ,
, ![]() , як абстрактна функція параметра
, як абстрактна функція параметра ![]() із
значеннями в просторі
із
значеннями в просторі ![]() , диференційовна по
, диференційовна по ![]() .
.
Лема 3. Нехай
узагальнена функція 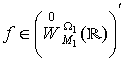 – згортувач у
просторі
– згортувач у
просторі ![]() ,
, ![]() . Тоді граничне
співвідношення
. Тоді граничне
співвідношення ![]() ,
, ![]() , виконується у просторі
, виконується у просторі 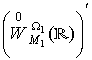 .
.
Лема 3 дозволяє для рівняння (1) задати початкову умову
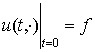 , (2)
, (2)
де f
– узагальнена функція з простору 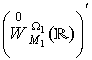 .
.
Під розв’язком задачі Коші (1), (2) розуміємо розв’язок рівняння (1),
який задовольняє початкову умову (2) у тому сенсі, що ![]() при
при ![]() у просторі
у просторі 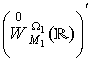 .
.
Символом 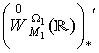 позначимо сукупність
узагальнених функцій з простору
позначимо сукупність
узагальнених функцій з простору 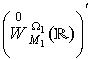 , які є згортувачами в просторі
, які є згортувачами в просторі ![]() . Основний результат містить наступне твердження.
. Основний результат містить наступне твердження.
Теорема 2. Задача
Коші (1), (2) коректно розв’язна,
розв’язок зображається у вигляді згортки:![]() ,
, 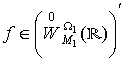 ,
, ![]() ,
, ![]() , при кожному
, при кожному ![]() .
.
Література:
1.
Крехивский В. В., Матийчук М. И. Фундаментальные решения и задача Коши
для линейных параболических систем с оператором Бесселя // Докл. АН СССР. – 1968. – Т. 181, №6. – С. 1320-1323.
2.
Ивасишен С. Д., Лавренчук В. П. Об интегральном представлении решений
параболической системы с оператором Бесселя // Нелинейные граничные задачи. –
1992. – Вып. 4. – С. 19-25.
3.
Житомирский Я. И. Задача
Коши для систем линейных уравнений в частных производных с дифференциальным
оператором Бесселя // Матем. сб. – 1955. – Т. 36, №2. – С. 299-310.
4.
Городецький В. В.,
Житарюк І. В. Задача Коші для одного класу параболічних систем з оператором
Бесселя в просторах узагальнених функцій //
Доп. АН УРСР. – 1991. – №7. – С. 20-23.
5.
Городецкий В.
В., Житарюк И. В., Лавренчук В. П. Задача Коши для линейных параболических
уравнений с оператором Бесселя в пространствах обобщенных функций типа S'. Черновицкий университет. – Черновцы, 1993. – 29 с. – Библиогр.
10 назв. – Рус. – Деп. в Укр ИНТЭИ 09.03.03, №388 – Ук 93.
6.
Гельфанд И. М., Шилов Г.
Е. Пространства основных и обобщенных функций. – М.: Физматгиз, 1958. – 307 с.
7.
Гуревич Б. Л. Некоторые
пространства основных и обобщенных функций и проблема Коши для
конечно-разностных схем // Докл. АН СССР. – 1954. – Т. 99, № 6. – С. 893-896.