Математика/1.Дифференциальные
и интегральные уравнения
Д.ф.-м.н. Городецький В. В.
Чернівецький
національний університет імені Юрія Федьковича,Україна
Багатоточкова за часом
задача для одного класу еволюційних псевдодиференціальних рівнянь
При побудові загальної теорії крайових задач, математичному моделюванні
задач, що виникають у теорії періодичних хвилеводів, біології, фізиці ядерних
реакцій, демографічних дослідженнях, при вивченні коливань різних систем
виникають нелокальні крайові задачі для диференціально-операторних рівнянь та
рівнянь з частинними похідними.
Дослідженням нелокальних крайових задач у різних аспектах займалося
багато математиків, використовуючи при цьому різні методи й підходи (О.О.
Дезін, В.К. Романко, С.Г. Крейн, В.М. Борок, Б. Й. Пташник, О.А. Самарський,
А.Н. Нахушев, В.І. Чесалін та ін.). Одержані важливі результати щодо
постановки, коректної розв’язності та побудови розв’язків, досліджені питання
залежності характеру розв’язності задач від поведінки символів операцій,
сформульовані умови регулярності та нерегулярності крайових умов для важливих
випадків диференціально-операторних рівнянь. Крайову задачу з багатоточковими
умовами в циліндричній області для загального ![]() -параболічного рівняння дослідив М. І. Матійчук [1]. Двоточкова за часом задача для
рівняння теплопровідності та
-параболічного рівняння дослідив М. І. Матійчук [1]. Двоточкова за часом задача для
рівняння теплопровідності та ![]() -параболічного рівняння зі сталими коефіцієнтами також
досліджена в [1]. Тут досліджується багатоточкова за часом задача для
еволюційного рівняння
-параболічного рівняння зі сталими коефіцієнтами також
досліджена в [1]. Тут досліджується багатоточкова за часом задача для
еволюційного рівняння
![]()
![]() , (1)
, (1)
де ![]() – псевдобесселевий
оператор, побудований за однорідним негладким у точці 0 символом (функцією
– псевдобесселевий
оператор, побудований за однорідним негладким у точці 0 символом (функцією ![]() ), у класі крайових умов з простору узагальнених функцій типу розподілів (
), у класі крайових умов з простору узагальнених функцій типу розподілів (![]() та
та ![]() – пряме та обернене перетворення Бесселя). Зазначимо, що
задача Коші для еволюційних рівнянь (1), а також для рівнянь вигляду (1), але з
оператором
– пряме та обернене перетворення Бесселя). Зазначимо, що
задача Коші для еволюційних рівнянь (1), а також для рівнянь вигляду (1), але з
оператором ![]() , досліджена в [2-4].
, досліджена в [2-4].
Наведемо основні означення, що
стосуються топологічної структури просторів основних та узагальнених функцій.
Нехай ![]() – фіксоване число з множини
– фіксоване число з множини ![]() ,
, ![]() – фіксоване число з
множини
– фіксоване число з
множини ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Символом
. Символом ![]() позначатимемо простір, елементами якого, за означенням, є
нескінченно диференційовні на
позначатимемо простір, елементами якого, за означенням, є
нескінченно диференційовні на ![]() функції, які
задовольняють нерівності
функції, які
задовольняють нерівності
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
У ![]() вводиться структура
зліченно-нормованого простору за допомогою норм
вводиться структура
зліченно-нормованого простору за допомогою норм ![]() ,
, ![]() де
де ![]() ,
, ![]() – фіксований
параметр.
– фіксований
параметр.
У просторі ![]() визначені і
неперервні операції зсуву аргументу та диференціювання.
визначені і
неперервні операції зсуву аргументу та диференціювання.
Символом
![]() позначатимемо
сукупність усіх парних функцій з простору
позначатимемо
сукупність усіх парних функцій з простору ![]() . Оскільки
. Оскільки ![]() утворює підпростір
утворює підпростір ![]() , то в
, то в ![]() природним способом
вводиться топологія. Цей простір з відповідною топологією називатимемо
основним, а його елементи – основними функціями. На функціях з простору
природним способом
вводиться топологія. Цей простір з відповідною топологією називатимемо
основним, а його елементи – основними функціями. На функціях з простору ![]() визначене
перетворення Бесселя
визначене
перетворення Бесселя ![]() :
:
![]()
де ![]() – нормована функція
Бесселя, при цьому
– нормована функція
Бесселя, при цьому ![]() – парна, обмежена,
неперервна на
– парна, обмежена,
неперервна на ![]() і нескінченно диференційовна
на
і нескінченно диференційовна
на ![]()
![]() функція. У функції
функція. У функції ![]()
![]() існують скінченні
односторонні границі
існують скінченні
односторонні границі ![]() функція
функція ![]()
![]() у точці
у точці ![]() має усувний розрив,
функції з простору
має усувний розрив,
функції з простору ![]() задовольняють умову:
задовольняють умову:
![]()
![]()
![]()
![]() ,
,
перетворення Бесселя відображає ![]() на
на ![]() взаємно однозначно і
неперервно [5].
взаємно однозначно і
неперервно [5].
Символом
![]() позначимо оператор
узагальненого зсуву аргументу, який відповідає оператору Бесселя
позначимо оператор
узагальненого зсуву аргументу, який відповідає оператору Бесселя ![]()
![]() :
:
![]()
![]()
де ![]() (
(![]() –
гамма-функція), при цьому
–
гамма-функція), при цьому ![]() . Оператор
. Оператор ![]() визначений і
неперервний у просторі
визначений і
неперервний у просторі ![]() , а операція
, а операція ![]()
![]()
![]() є нескінченно
диференційовною у цьому просторі, тобто граничні співвідношення вигляду
є нескінченно
диференційовною у цьому просторі, тобто граничні співвідношення вигляду
![]()
справджуються за топологією простору ![]() .
.
Символом
![]() позначатимемо
простір, топологічно спряжений до
позначатимемо
простір, топологічно спряжений до ![]() , елементи цього простору називатимемо узагальненими
функціями. Кожна узагальнена функція
, елементи цього простору називатимемо узагальненими
функціями. Кожна узагальнена функція 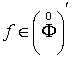 має скінченний
порядок, тобто
має скінченний
порядок, тобто 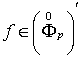 при деякому
при деякому ![]() (яке називають
порядком
(яке називають
порядком ![]() ), де –
), де – ![]() поповнення
поповнення ![]() за нормою
за нормою ![]() .
.
Оскільки в просторі ![]() визначена операція
узагальненого зсуву аргументу, згортку узагальненої функції
визначена операція
узагальненого зсуву аргументу, згортку узагальненої функції 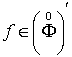 з основною функцією
задамо формулою
з основною функцією
задамо формулою ![]() (індекс
(індекс ![]() у
у ![]() означає, що функціонал
означає, що функціонал ![]() діє на основну функцію за змінною
діє на основну функцію за змінною ![]() ), при цьому
), при цьому ![]() є нескінченно диференційовною на
є нескінченно диференційовною на ![]() функцією. Якщо
функцією. Якщо 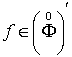 ,
, ![]()
![]() ,
, ![]()
![]() , і із співвідношення
, і із співвідношення ![]() при
при ![]() за топологією простору
за топологією простору ![]() випливає, що
випливає, що ![]() при
при ![]() за топологією простору
за топологією простору ![]() , то функціонал
, то функціонал ![]() називається згортувачем у просторі
називається згортувачем у просторі ![]() . Перетворення Бесселя узагальненої функції
. Перетворення Бесселя узагальненої функції 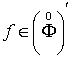 визначається за
допомогою співвідношення
визначається за
допомогою співвідношення ![]() ,
, ![]()
![]() , при цьому
, при цьому ![]()
![]() . Якщо узагальнена функція
. Якщо узагальнена функція 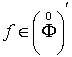 – згортувач у
просторі
– згортувач у
просторі ![]() , то для довільної функції
, то для довільної функції ![]()
![]() правильною є формула:
правильною є формула:
![]() .
.
Нехай ![]() :
: ![]()
![]() – неперервна, парна на
– неперервна, парна на ![]() функція, однорідна
порядку
функція, однорідна
порядку ![]() , яка: 1)
нескінченно диференційовна при
, яка: 1)
нескінченно диференційовна при ![]() ; 2) похідні
функції
; 2) похідні
функції ![]() задовольняють умову:
задовольняють умову: ![]()
![]()
![]()
![]()
![]() :
: ![]() ; 3)
; 3) ![]()
![]()
![]() :
: ![]() .
.
Зазаначимо,
що з накладених умов на функцію ![]() випливає, що
випливає, що ![]() – мультиплікатор у просторі
– мультиплікатор у просторі ![]() . Нехай
. Нехай ![]()
![]()
![]() – псевдобесселевий
оператор, побудований за символом
– псевдобесселевий
оператор, побудований за символом ![]() , тобто
, тобто ![]() ,
, ![]()
![]() . Для еволюційного рівняння (1) розглянемо нелокальну
багатоточкову за часом задачу
. Для еволюційного рівняння (1) розглянемо нелокальну
багатоточкову за часом задачу
![]() (2)
(2)
де ![]() ,
, ![]() ,
, ![]() – фіксовані
параметри,
– фіксовані
параметри, ![]() ,
, ![]() . Класичний розв’язок
. Класичний розв’язок ![]() задачі (1), (2)
шукаємо за допомогою перетворення Бесселя, у результаті чого знайдемо, що
задачі (1), (2)
шукаємо за допомогою перетворення Бесселя, у результаті чого знайдемо, що
![]() ,
, ![]() ,
, 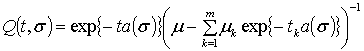 ,
, ![]() ,
, ![]()
![]() .
.
Властивості функції ![]() визначаються
властивостями функції
визначаються
властивостями функції ![]() .
.
Лема 1. При фіксованому ![]() функція
функція ![]() нескінченно
диференційовна по
нескінченно
диференційовна по ![]()
![]()
![]() ; для її похідних сравджуються оцінки
; для її похідних сравджуються оцінки
![]() ,
, ![]()
![]() ,
, ![]() , (3)
, (3)
де ![]() – сталі, незалежні
від
– сталі, незалежні
від ![]() ,
, ![]() ,
, ![]() , якщо
, якщо ![]() ,
, ![]() , якщо
, якщо ![]() ,
, ![]() .
.
Із оцінок (3) випливає, що ![]() , як функція аргументу
, як функція аргументу ![]() , при кожному
, при кожному ![]() є елементом простору
є елементом простору ![]() . Тоді
. Тоді ![]() , як функція
, як функція ![]() , є елементом простору
, є елементом простору ![]() (при кожному
(при кожному ![]() ). Крім того,
). Крім того, ![]() – парна функція аргументу
– парна функція аргументу ![]() (при фіксованому
(при фіксованому ![]() ), неперервно диференційовна функція аргументу
), неперервно диференційовна функція аргументу ![]() (при фіксованому
(при фіксованому ![]() ). Інші властивості функції
). Інші властивості функції ![]() описують наступні
твердження.
описують наступні
твердження.
Теорема 1. Для функції ![]() та її похідних (за змінною
та її похідних (за змінною ![]() ) правильними є оцінки:
) правильними є оцінки: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() , де стала
, де стала ![]() не залежить від
не залежить від ![]() .
.
Теорема 2. ![]() при
при ![]() у просторі
у просторі ![]() (тут
(тут ![]() – дельта-функція
Дірака,
– дельта-функція
Дірака, ![]() ).
).
Теорема 3. Функція ![]() ,
, ![]() , як абстрактна функція параметра
, як абстрактна функція параметра ![]() із значеннями в
просторі
із значеннями в
просторі ![]() , диференційовна по
, диференційовна по ![]() .
.
Символом ![]() позначимо клас
узагальнених функцій з
позначимо клас
узагальнених функцій з ![]() , які є згортувачами у просторі
, які є згортувачами у просторі ![]() .
.
Лема 2. Нехай ![]() ,
, 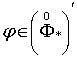 ,
,![]() . Тоді у просторі
. Тоді у просторі ![]() справджується граничне
співвідношення
справджується граничне
співвідношення
![]() .
.
Надалі функцію ![]() називатимемо
фундаментальним розв’язком багатоточкової задачі (ФРБЗ) для рівняння (1). З
леми 2 випливає, що для рівняння (1) багатоточкову за часом задачу можна
ставити так: знайти розв’язок
називатимемо
фундаментальним розв’язком багатоточкової задачі (ФРБЗ) для рівняння (1). З
леми 2 випливає, що для рівняння (1) багатоточкову за часом задачу можна
ставити так: знайти розв’язок ![]() рівняння (1), який
узальнює граничну умову
рівняння (1), який
узальнює граничну умову
![]() ,
, 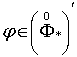 , (4)
, (4)
де границі розглядаються у просторі ![]() (обмеження на
параметри
(обмеження на
параметри ![]()
![]() такі ж, як і у
випадку задачі (1), (2)).
такі ж, як і у
випадку задачі (1), (2)).
Основний результат складає
наступне твердження.
Теорема 4. Задача (1), (4) коректно розв’язна.
Розв’язок зображається у вигляді згортки:
![]() ,
, ![]() ,
,
де ![]() – ФРБЗ для рівняння (1).
– ФРБЗ для рівняння (1).
Література:
1.
Матійчук М.І.
Параболічні сингулярні крайові задачі. – Київ: Інститут математики НАН України,
1999. – 170 с.
2.
Городецький В.
В., Ленюк О. М. Еволюційні рівняння з псевдобесселевими операторами // Доп. НАН
України. – 2007. – №8. – С. 11-15.
3.
Ленюк О. М.
Задача Коші для еволюційних рівнянь з псевдобесселевими операторами // Науковий
вісник Чернівецького університету: Зб. наук. пр. Вип. 349. Математика. –
Чернівці: Рута, 2007. – С. 55-65.
4.
Шевчук Н. М.
Задача Коші для еволюційних рівнянь з псевдобесселевими операторами
нескінченного порядку // Науковий вісник Чернівецького університету: Зб. наук.
пр. Вип. 374. Математика. – Чернівці: Рута, 2008. – С. 145-154.
5.
Городецький В. В.
Задача Коші для еволюційних рівнянь нескінченного порядку. – Чернівці: Рута,
2005. – 291 с.