Математика/Математическое моделирование

Аспирант ПензГТУ Мокроусов Д.А., студент ПГУ Демин Е.С.,
к.т.н. Карпухин Э.В., д.т.н. Демин С.Б.

Пензенский государственный технологический университет (ПензГТУ)
Пензенский государственный университет (ПГУ)

Повышение эффективности численных методов при моделировании магнитострикционных уровнемеров накладного типа со сложной геометрией акустического тракта

Аннотация: Предлагается способы повышения эффективности при численном моделировании магнитных полей накладных магнитострикционных преобразователей уровня (НМПУ) для байпасных систем со сложной геометрией акустического тракта

Ключевые слова: накладные магнитострикционные преобразователи уровня, численные методы

При проведении математического моделирования магнитных полей НМПУ, возникает задача решения систем конечно-разностных уравнений с большим числом неизвестных. Такая задача была сформулирована и решена в работах многих авторов, например [1-3]. Определение искомых магнитных потенциалов проводилось с применением численных методов, требующих значительных вычислительных ресурсов и времени при моделировании НМПУ со сложной геометрией акустического тракта для байпасных систем.

Однако, практика решения систем уравнений подобных по своей структуре конечно-разностным уравнениям, получаемым для магнитного поля НМПУ, позволяет выработать некоторые способы сокращения времени расчета при сохранении точности результата [2,3].

Так время, расходуемое на решение системы конечно-разностных уравнений итерационным методом, сильно зависит от того, насколько близко были выбраны начальные приближения к истинным значениям неизвестных. Если начальные значения переменных близки к истинным, то временем, затрачиваемым на решение системы, практически можно пренебречь. Поэтому одним из способов повышения эффективности итерационных методов является выбор хорошего начального приближения. Это может быть осуществлено, например, с использованием различных систем моделирования магнитных полей таких как ELCUT, Littlemag, Ansys и др. Эти системы имеют ряд недостатков, ограничивающие их использование для комплексного моделирования НМПУ, но предварительные результаты, полученные с их помощью, можно считать наиболее близкими к истинным значениям [3]. Выбор их в качестве начальных приближений позволит существенно сократить время решения.

Другим способом отыскания начальных приближений может служить предварительный расчет поля на сетке с меньшим числом узлов. Полученные в результате потенциалы с помощью интерполяционных формул переносятся на узлы требуемой, более мелкой сетки [2,4].

При проведении многовариантных расчетов с целью выбора оптимальных геометрических параметров исследуемого устройства, в качестве начальных значений потенциала удобно использовать те, что были получены при расчете предыдущего варианта, соответствующие расчетной области с похожей геометрией.

При использовании итерационных методов с искусственным ускорением сходимости, например метода верхней релаксации [2,3], известен способ сокращения числа итераций, путем выбора на каждом шаге нового оптимального значения коэффициента ускорения сходимости . Введение набора позволяет сократить общее число итераций , а, следовательно, и время, затрачиваемое на поиск решения. Способы получения набора оптимальных значений коэффициента ускорения сходимости приведены в [2,4].

Таким образом, отыскание начальных значений магнитных потенциалов, тем или иным методом, близких к истинным, и введение набора оптимальных значений коэффициента ускорения сходимости, позволит существенно снизить временные затраты на расчет магнитных полей НМПУ со сложной геометрией акустического тракта.

Другим способом повышения эффективности численных методов, является увеличение точности результата при неизменном времени расчета.

Одним из эффективных методов повышения точности является экстраполяционный метод, основанный на решении той же задачи, но с использованием последовательности сеток. Суть метода заключается в использовании приближенных решений на последовательности сгущающихся сеток, чтобы найти решение с более высокой точностью. Так для получения некоторого решения с погрешностью порядка следует решить задачу на сетках с шагами , т.е. найти приближений . Искомое решение тогда может быть найдено по формуле

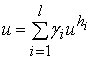, (1)

где – коэффициенты, удовлетворяющие системе уравнений

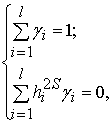(2)

здесь [2].

Так с использованием данного метода, имея решения на сетках с шагами соответственно, можно с легкостью получить решение с погрешностью порядка . Для этого необходимо составить и решить систему (3.38) при . В результате получим . Следовательно имеем следующее выражение .

Таким образом, для уменьшения порядка погрешности в два раза, требуется произвести расчет на двух сетках с шагами с последующим составлением линейной комбинации этих решений. Для такого же увеличения точности путем простого измельчения сетки потребовалось бы уменьшить её шаг от значения до , то есть в 100 раз. Отсюда следует, что применение рассмотренного метода, основанного на выражениях (1), (2), позволяет существенно повысить точность и сократить время, требуемое для расчета.

Другим способом увеличения точности при расчете магнитного поля НМПУ со сложной геометрией акустического тракта, является применение разностной аппроксимации с использованием производных высокого порядка, а также выбор сложного контура интегрирования при составлении конечно-разностных уравнений методом баланса [4].

При этом могут быть использованы следующие известные схемы [2], приведенные на рисунке 1.

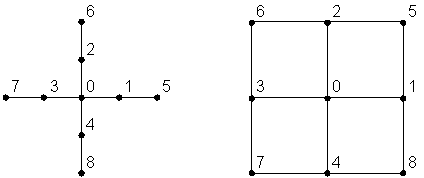
а) б)

Рисунок 1 – Схемы для получения разностных уравнений с более высокой точностью аппроксимации

Так при использовании схемы «большой крест» (рисунок 1а) могут быть получены уравнения, объединяющие потенциалы девяти соседних точек вида

, (3)

где – искомый магнитный потенциал k-ого узла сетки, – плотность тока проводимости 0-ого узла.

Это выражение имеет порядок погрешности , что является в четыре раза выше, чем при использовании простой пятиточечной аппроксимации, имеющей погрешность порядка [3].

Более высокий порядок погрешности дает схема «ящик» (рисунок 2б). Соответствующая этой схеме разностная аппроксимация имеет погрешность , и имеет вид

. (4)

Таким образом, применение рассмотренных в данной статье способов, в составе известных численных методов позволит значительно повысить их эффективность и сократить время решения рассматриваемой задачи моделирования НМПУ со сложного геометрией акустического тракта.

Литература:

1. Демин С.Б. Магнитострикционные системы для автоматизации технологического оборудования: Монография. – Пенза: ИИЦ ПГУ, 2002. – 182 с.

2. Демирчян К.С., Чечурин В.Л. Машинные расчеты электромагнитных полей. – М.: Высшая школа, 1986. – 240 с.

3. Карпухин Э.В., Демин Е.С, Демин С.Б. К вопросу применения эффективных численных методов для моделирования магнитострикционных приборов уровня. Вестник Тамбовского государственного технического университета. – 2012. – Т.18. – №11. – С.58-64.

4. Самарский А.А., Гулин А.В. Численные методы. – М: Наука, 1989. – 432 с.